Az egész Föld optimális ábrázolása általános torzulású pólusvonalas képzetes hengervetületben
A világtérképek vetülete – a XX. század elejére kialakult hagyományoknak megfelelõen, amelyek a torzulások mérlegelésén, az övezetes földrajzi jelenségek kihangsúlyozásán, szemléletességi és esztétikai követelményeken alapultak – többnyire képzetes hengervetület. A térképészet története folyamán igen sok képzetes hengervetület keletkezett, az ezek közötti minõsítés és válogatás a fenti szempontok alapján történik, különös tekintettel a torzulási viszonyokra.
A szélességi köröket párhuzamos egyenesként megjelenítõ képzetes hengervetületek között az ábrázolt témától függõen mind területtartó, mind általános torzulású változatok elõfordulnak, de a korábban domináns területtartó vetületekkel szemben napjainkban – a kontinensek alakjának kisebb torzulása miatt – az általános torzulású vetületek kerülnek elõtérbe. A pólust, ahol a torzulások egy része végtelen naggyá válik, a képzetes hengervetület vagy egy pontra, v
agy egy egyenes szakaszra (az úgynevezett pólusvonalra) képezi le. A póluspontos változat általában szemléletesebb és esztétikusabb; a pólusvonalas változat megértése absztrakciós képességet kíván, viszont a pólusvonal környékén a torzulások csökkenthetõk.
Egy -
az egész Földet mind az x, mind pedig az y tengelyre nézve szimmetrikusan ábrázoló -
térkép vetületét akkor tekintjük egy bizonyos torzulás szempontjából legjobbnak, ha az adott torzulást, pontosabban torzultságot jellemzõ mérõszámnak a –85° és 85° szélességi körök közé esõ területen (azaz a pólusok környékétõl eltekintve az egész Földön) számított átlaga a lehetõ legkisebb. Esetünkben – vagyis az általános torzulású vetületek körében – az ún. teljes torzultság ![]() 2 lokális mérõszámainak átlagát kell minimálissá tenni. Ezek a torzultsági mérõszámok (ld. [4]) az adott pontban fellépõ maximális a és minimális b hossztorzulás függvényei:
2 lokális mérõszámainak átlagát kell minimálissá tenni. Ezek a torzultsági mérõszámok (ld. [4]) az adott pontban fellépõ maximális a és minimális b hossztorzulás függvényei:
![]() (Airy, James és Clarke mérõszáma [1] és [6] alapján)
(Airy, James és Clarke mérõszáma [1] és [6] alapján)
![]() (Airy eredeti mérõszáma a [1] alapján)
(Airy eredeti mérõszáma a [1] alapján)
![]() (Airy módosított mérõszáma [5] alapján)
(Airy módosított mérõszáma [5] alapján)
![]() (Airy-Kavrajszkij féle mérõszám [7] alapján)
(Airy-Kavrajszkij féle mérõszám [7] alapján)
(A szakirodalomban elõfordul, hogy
Az a és b extremális hossztorzulásokat a fokhálózatmenti torzulásokból: a h parallelkörmenti és k meridiánmenti hossztorzulásból, valamint a fokhálózati vonalak által bezárt ![]() szögbõl számítjuk az
szögbõl számítjuk az
![]() és
és ![]() képletekkel. Legyenek y=y(j
) és x=x(j
,l
) a képzetes hengervetület egyenletei; ezekbõl a fokhálózatmenti torzulások a
képletekkel. Legyenek y=y(j
) és x=x(j
,l
) a képzetes hengervetület egyenletei; ezekbõl a fokhálózatmenti torzulások a
![]() ,
, 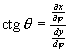 és
és 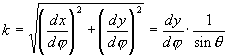
képletekbõl számíthatók minden
Az egész Földre az átlagos teljes torzultság (globális) ![]() 2 mérõszámát az
2 mérõszámát az
![]()
felületi integrálból vont négyzetgyök adja, ahol ![]() a -
85° és 85° szélességi körök közé esõ gömböv (ld. [4]), m
(T) pedig e gömböv felszíne az egység sugarúnak tekintett gömbön. Minthogy e
2 a-n és b-n keresztül j
-tõl és l
-tól függ,
a -
85° és 85° szélességi körök közé esõ gömböv (ld. [4]), m
(T) pedig e gömböv felszíne az egység sugarúnak tekintett gömbön. Minthogy e
2 a-n és b-n keresztül j
-tõl és l
-tól függ, ![]() az alábbi alakban írható fel:
az alábbi alakban írható fel:
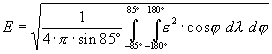
A fenti e 2 mérõszámok alapján így kapjuk az EAJ (Airy-James-Clarke féle), az EAe (Airy eredeti), az EAm (Airy módosított) és az EAK (Airy-Kavrajszkij féle) torzultsági kritériumokat. Általános torzulású vetületeket tehát a teljes torzultság szempontjából úgy hasonlíthatunk össze, hogy valamelyik kritérium-értékét minden összehasonlítandó vetületre kiszámítjuk, és a kisebb kritérium-értékû vetületet tekintjük jobbnak. Legjobbnak ("optimálisnak") azt a vetületet nevezzük, amelynek kritérium-értéke a vizsgált vetület-halmazon belül a legkisebb (ld. [10], [4]).
A pólusvonalas képzetes hengervetületeknek a meridiánvonalak jellegétõl független, matematikai szempontú osztályozását a vetületi egyenletek alapján végezzük, éspedig a valódi hengervetületekbõl kiindulva. Az osztályozás elsõdleges szempontja az
x=x(j ,l ) vetületi egyenlet, mivel döntõen ez adja meg a vetület jellegét megszabó kontúrvonalat. (Az y=y(j ) a kontúrt csak kis mértékben befolyásolja.)
A valódi hengervetületeknél az x vetületi egyenlet csak l
-tól függ, ezért a parallelkörök képei mind egyenlõ hosszúságúak: hosszuk x=arcl
esetén a hossztartó egyenlítõ hosszával, ![]() (c<1) esetén pedig két hossztartó parallelkör hosszával egyenlõ. A képzetes hengervetületeknél az x vetületi egyenlet l
-n kívül j
-tõl is függ:
(c<1) esetén pedig két hossztartó parallelkör hosszával egyenlõ. A képzetes hengervetületeknél az x vetületi egyenlet l
-n kívül j
-tõl is függ:
A y=y(j ) vetületi egyenlet jellege képezi a képzetes hengervetületek másodlagos osztályozási szempontját:
A legjobb képzetes hengervetületeket az x=x(j ,l ) vetületi egyenlet fenti csoportjaihoz határoztuk meg, és minden csoporton belül vizsgáltuk az y=y(j ) függvény szerint képzett alcsoportokhoz tartozó vetületeket. Az x=x(j ,l ) alkotó függvényeit, valamint az y=y(j ) függvényt j illetve l polinomjaival közelítettük, éspedig y-t j -ben páratlan kitevõs, x alkotó függvényeit pedig j -ben páros, l -ban páratlan kitevõs hatványokat tartalmazó polinomokkal. A tapasztalat szerint az egész Földet ábrázoló legjobb képzetes hengervetületeknél 3 együtthatós polinom minden függvényhez elegendõ pontosságú közelítést eredményezett, sõt a harmadik tag figyelembevételére sem mindig volt szükség.
A számításokhoz a gömbfelület –85° és 85° szélesség közötti részét 1°-os fokhálózattal bontottuk fel, majd a fokhálózati metszéspontokban kiszámoltuk a h parallelkör menti és a k meridián menti hossztorzulásokat, valamint a q térképi fokhálózati szög kotangensét, ezekbõl pedig az a és b extremális hossztorzulásokat a fentiekben megadott képletek segítségével. Végül a lokális teljes torzultság e 2 =e 2(a,b) mérõszámainak a fokhálózati metszéspontokra kiszámított értékeket a kétváltozós Simpson formulával (ld. [8]) összegezve és az alapfelületi felszínnel osztva kapjuk az átlagos torzultság EAJ, EAe, EAm és EAK kritériumok értékeit.
Látható, hogy a E mennyiségek az integrált e 2 =e 2(a,b) mennyiségeken keresztül függnek a vetületi egyenletekben szereplõ együtthatóktól. A minimális E értékeket szolgáltató együttható-értékeket a variációszámítás direkt módszerével, a “szimplex módszer” nevû közelítõ minimalizáló eljárás segítségével határoztuk meg (ld. [9], [11]).
A valódi, majd a képzetes hengervetületek x=x(j ,l ) szerint definiált osztályaiban és y=y(j ) szerinti alosztályaiban az itt következõ eredményeket kaptuk.
I. Legjobb valódi hengervetületek hossztartó egyenlítõvel
x=arcl
esetén ![]() , a fokhálózat merõlegessége miatt ctgq
=0. A variációszámítás egyszerû alkalmazásával kimutatható (ld. [5]), hogy mind a négy vizsgált kritérium szerinti legjobb valódi hengervetület meridiánban hossztartó. Az y vetületi egyenlet tehát ebben az esetben mindig y=arcj
alakú, vagyis k=1.
, a fokhálózat merõlegessége miatt ctgq
=0. A variációszámítás egyszerû alkalmazásával kimutatható (ld. [5]), hogy mind a négy vizsgált kritérium szerinti legjobb valódi hengervetület meridiánban hossztartó. Az y vetületi egyenlet tehát ebben az esetben mindig y=arcj
alakú, vagyis k=1.
A kritériumok értékei:
1. táblázat
|
EAJ=0,76317 |
|
EAe=1,52635 |
|
EAm=1,52635 |
|
EAK=0,34552 |
(h³ k, emiatt itt EAe=EAm).
II. Legjobb valódi hengervetületek két hossztartó parallelkörrel
x=c×
arcl
(c<
1) esetén két hossztartó parallelkör van (±
j
n); ![]() és ctgq
=0. Ekkor az EAJ, EAm és EAK kritériumok szerinti legjobb hengervetület továbbra is meridiánban hossztartó (vagyis y=arcj
és k=1), azonban a hossztartó parallelkörök optimális helyzete kritériumonként különbözik. Más a helyzet az EAe szerinti legjobb hengervetülettel. Ha itt is a meridiánban hossztartó (k=1) változattal számolunk, akkor az eredmények az alábbi táblázatban foglalhatók össze:
és ctgq
=0. Ekkor az EAJ, EAm és EAK kritériumok szerinti legjobb hengervetület továbbra is meridiánban hossztartó (vagyis y=arcj
és k=1), azonban a hossztartó parallelkörök optimális helyzete kritériumonként különbözik. Más a helyzet az EAe szerinti legjobb hengervetülettel. Ha itt is a meridiánban hossztartó (k=1) változattal számolunk, akkor az eredmények az alábbi táblázatban foglalhatók össze:
2. táblázat
|
Optimális |
||
|
c |
j n |
|
|
EAJ=0,38370 |
0,47377 |
± 61,72° |
|
EAe=0,89928 |
0,59260 |
± 53,66° |
|
EAm=0,95459 |
0,63234 |
± 50,78° |
|
EAK=0,27448 |
0,74320 |
± 42,00° |
Az EAe értéke azonban csökkenthetõ, ha az y-t háromparaméteres, ötödfokú polinomnak tekintjük (y=y1× arcj +y2× arc3j +y3× arc5j ). Direkt módszerrel ekkor a következõ eredményt kapjuk:
EAe=0,78361 , c=0,46021 (j n =62,60°)
y1=0,51700 , y2× =0,17995 , y3=- 0,02942
A variációszámításból ismert Euler–Lagrange féle differenciálegyenlettel (ld. [9]) kimutatható, hogy az EAe kritérium szerinti legjobb, két parallelkörben hossztartó valódi hengervetület a normálparallelkörökön kívül meridiánban hossztartó, azok között viszont az y vetületi egyenletet az
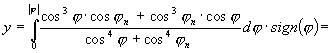
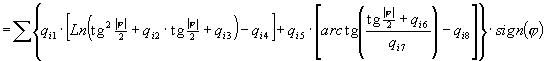
képlet adja meg, ahol sign(j ) a földrajzi szélesség elõjelét jelenti (melyet az É-i félgömbön tekintünk pozitívnak). Ha az egész Földet akarjuk ábrázolni, akkor a qij (i,j=1,…,8) értékeket a 3. táblázat szerint kell megadni, és normálparallelkörnek a ± 62.8° szélesség választandó. Ekkor EAe=0,78267, és a valódi hengervetületek körében ez a kritérium-érték tovább már nem csökkenthetõ (ld. [5]).
3. táblázat
|
qij |
j=1 |
j=2 |
j=3 |
j=4 |
j=5 |
j=6 |
j=7 |
j=8 |
|
i=1 |
0,11246 |
1,39784 |
0,55061 |
-0,59672 |
-0,02325 |
0,69892 |
0,24925 |
1,22823 |
|
i=2 |
-0,11246 |
-1,39784 |
0,55061 |
-0,59672 |
-0,02325 |
-0,69892 |
0,24925 |
-1,22823 |
|
i=3 |
0,11246 |
2,53869 |
1,81615 |
0,59672 |
0,02325 |
1,26935 |
0,45268 |
1,22823 |
|
i=4 |
-0,11246 |
-2,53869 |
1,81615 |
0,59672 |
0,02325 |
-1,26935 |
0,45268 |
-1,22823 |
|
i=5 |
0,01162 |
1,39784 |
0,55061 |
-0,59672 |
0,22492 |
0,69892 |
0,24925 |
1,22823 |
|
i=6 |
-0,01162 |
-1,39784 |
0,55061 |
-0,59672 |
0,22492 |
-0,69892 |
0,24925 |
-1,22823 |
|
i=7 |
0,01162 |
2,53869 |
1,81615 |
0,59672 |
-0,22492 |
1,26935 |
0,45268 |
1,22823 |
|
i=8 |
-0,01162 |
-2,53869 |
1,81615 |
0,59672 |
-0,22492 |
-1,26935 |
0,45268 |
-1,22823 |
A Föld képe az EAe kritérium szerinti legjobb valódi hengervetületben az 1. ábrán látható.
III. Legjobb pólusvonalas képzetes hengervetületek ekvidisztáns parallelkörökkel
Az x=c(j )× arcl vetületi egyenlettel leírt legegyszerûbb típusú képzetes hengervetületnél a
c(j ) függvényt c1 +c2× arc2j +c3× arc4j alakú polinommal közelítjük:
![]()
(A polinom fokszámának növelése az E értékét elenyészõ, 0.01%-nál kisebb mértékben csökkentené.) Ekkor a fokhálózat menti torzulások:
![]()
![]()
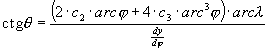
ahol ![]() értéke a közelítõ y=y(j
) polinom fokszámától függ:
értéke a közelítõ y=y(j
) polinom fokszámától függ:
Meghatároztuk az optimális vetületi paramétereket y=arcj , valamint elsõ-, harmad- és ötödfokú közelítõ polinom esetében. Hasonlítsuk össze az y=arcj (4. táblázat) és y=y1× arcj +y2× arc3j +y3× arc5j (5. táblázat) által szolgáltatott eredményeket az E kritériumok értékei alapján.
4. táblázat
|
E |
c1 |
c2 |
c3 |
|
EAJ=0,30810 |
0,63987 |
-0,14501 |
- |
|
EAe=0,72459 |
0,68075 |
-0,08296 |
-0,01733 |
|
EAm=0,75141 |
0,71518 |
-0,09915 |
-0,01389 |
|
EAK=0,24862 |
0,77798 |
-0,07086 |
-0,01880 |
5. táblázat
|
E |
c1 |
c2 |
c3 |
y1 |
y2 |
y3 |
|
EAJ=0,30773 |
0,64220 |
-0,15205 |
0,00282 |
1,00000 |
-0,01977 |
0,00462 |
|
EAe=0,68309 |
0,60451 |
-0,04140 |
-0,02866 |
0,71784 |
0,15347 |
-0,02927 |
|
EAm=0,74609 |
0,71861 |
-0,09752 |
-0,01764 |
0,98534 |
0,04594 |
-0,01038 |
|
EAK=0,24840 |
0,77900 |
-0,07136 |
-0,01950 |
1,00000 |
0,01247 |
-0,00238 |
Látható, hogy az EAJ és az EAK kritériumok tekintetében csak igen csekély, 0.01% körüli csökkenés érhetõ el az y fokszámának emelésével. Az EAm valamivel nagyobb mértékben, 0.7%-kal csökkent. Következésképpen az EAJ és EAK szerinti legjobb, ekvidisztáns képzetes hengervetületet célszerû középmeridiánban hossztartónak tekinteni, sõt még az EAm szerinti legjobb, ekvidisztáns képzetes hengervetülethez is elfogadható közelítés az y=arcj .
Igen jelentõs mértékben: 7%-kal csökkenthetõ vi
szont EAe az ötödfokú y bevezetésével, ami a középmeridián menti hossztorzulás változó voltát mutatja. A középmeridián tehát itt nem ekvidisztáns, az osztásközök az egyenlítõtõl a pólusok felé haladva a ± 71,86° szélességig fokozatosan nõnek, onnan a pólusokig kissé csökkennek.
A Föld képe az EAK kritérium szerint legjobb, ekvidisztáns parallelkörû pólusvonalas képzetes hengervetületben a 2. ábrán látható.
IV. Területtartó pólusvonalas képzetes hengervetület elõállítása a legjobb, ekvidisztáns parallelkörû képzetes hengervetületbõl a szélességek átszámozásával
Ismeretes (ld. [12]), hogy képzetes hengervetületeknél a t területi modulus az alábbi alakban számítható:
![]()
Tekintsünk most egy területtartó (t =1) képzetes hengervetületet. Ekkor fennáll a
![]() egyenlet, ahonnan
egyenlet, ahonnan ![]() következik. Vagyis
következik. Vagyis ![]() csak a j
szélesség függvénye, tehát az x=x(j
,l
) vetületi egyenlet l
-nak lineáris függvénye. Ebbõl adódóan a területtartó képzetes hengervetületek parallelkörei mindig ekvidisztánsak.
csak a j
szélesség függvénye, tehát az x=x(j
,l
) vetületi egyenlet l
-nak lineáris függvénye. Ebbõl adódóan a területtartó képzetes hengervetületek parallelkörei mindig ekvidisztánsak.
Az állítás fordítva természetesen nem igaz, azaz egy ekvidisztáns parallelkörû képzetes hengervetület nem feltétlenül területtartó (ld. pl. Eckert III. és V. vetületét). Ha viszont egy ekvidisztáns parallelkörû képzetes hengervetület az egész Földfelületet egy vele megegyezõ területû síkidomra képezi le, akkor a szélességi körök átszámozásával ("módosított földrajzi szélesség" bevezetésével) a vetület mindig területtartóvá alakítható. Ez a
transzformáció a meridiánokat (és ezzel a kontúrvonalat) nem változtatja meg, viszont megváltozhat a parallelköröknek az egyenlítõtõl vett távolsága.
Tegyük fel, hogy egy középmeridiánban hossztartó, parallelkörökben ekvidisztáns képzetes hengervetület y=arcj és x=x(j ,l ) egyenleteit egy alkalmasan megválasztott d arányossági tényezõvel beszorozva, az egész Föld képére vonatkozó területegyenlõség már fennáll. Alkalmazzuk erre a vetületre a y (j ) szélesség-átszámozást ( y=arcy és x=x(y ,l ) ) úgy, hogy minden - az ellipszis és a j szélességi kör által határolt - gömböv 2× p × sinj felszíne legyen egyenlõ a megfelelõ térképi idom területével. Képletben ez az alábbiakat jelenti (ld. 3. ábra):
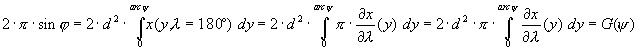 (Megjegyzendõ, hogy ebbõl a
(Megjegyzendõ, hogy ebbõl a ![]() alakú egyenlet által meghatározott y
(j
) implicit szélesség-átszámozási függvénybõl a y
nem mindig fejezhetõ ki.) Az átszámozott
alakú egyenlet által meghatározott y
(j
) implicit szélesség-átszámozási függvénybõl a y
nem mindig fejezhetõ ki.) Az átszámozott
d× arcy és d× x(y ,l ) egyenletekkel meghatározott vetület már területtartó, mert (felhasználva az implicit függvény deriválására vonatkozó formulát):
![]() =
=
![]() .
.
(Ha a parallelkörökben ekvidisztáns képzetes hengervetületben a középmeridián nem hossztartó, akkor elõször vezessük be a z
=z ( j ) módosított szélességet a![]()
képlet segítségével. Az átszámozott y=y(z ) a z -ra nézve hossztartó; most már alkalmazhatunk egy újabb, y (z ) átszámozást y=y(z ) -ra a fenti y (j ) átszámozás mintájára. A két egymás utáni átszámozás és az esetleges d-szeres hasonlósági transzformáció együttes alkalmazásával tehát területtartó vetülethez jutunk.)
A fenti gondolatmenetet követve, készítsünk a szélességi körök átszámozásával területtartó képzetes hengervetületet pl. az EAm kritérium szerinti legjobb képzetes hengervetületbõl, melynek parallelkörei ekvidisztánsak, középmeridiánját pedig hossztartónak tekintjük. Elõször is határozzuk meg a hasonlósági transzformáció d konstansának értékét, melynek négyzete a gömb felszínének és a teljes Föld képét megadó síkidom területének hányadosa:
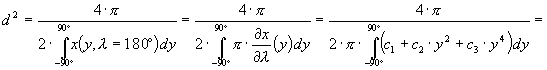
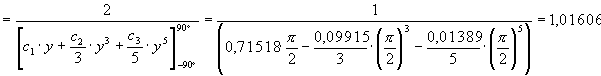
A vetületi egyenletek: y=0,955836× arcy
x=0,955836× (0,77798- 0,07086× arc2y - 0,01880× arc4y )× arcl
A y (j ) szélesség-átszámozási függvényt meghatározó egyenletet az egyenlítõ által határolt gömböveknek ugyanakkora területû síkidomra való leképezése adja:
![]()
vagyis ![]()
A 4. ábrán az EAK kritérium szerinti legjobb, ekvidisztáns parallelkörû pólusvonalas képzetes hengervetületbõl származtatott területtartó vetület látható.
V. Pólusvonalas képzetes hengervetületek ugyanolyan arányban felosztott parallelkörökkel
Az x=c(j )× f(l ) vetületi egyenlettel leírt képzetes hengervetületnél a c(j ) függvényt c1+c2× arc2j +c3× arc4j alakú polinommal, az f(l ) függvényt a arcl +f1× arc3l polinommal közelítjük:
![]()
Ebben a vetületosztályban az ekvidisztáns vetületekhez képest az E kritériumok értéke csak szerény mértékben csökkenthetõ tovább. Általánosan elmondható, hogy itt a meridiánban hossztartó közelítést már nem tekintjük elég pontosnak, az y vetületi egyenletet harmad- vagy ötödfokú polinommal közelítjük: y=y1× arcj +y2× arc3j (+y3× arc5j ) . A fokhálózat menti torzulások:
![]()
![]()
![]()
Az egyes kritériumok szerinti legjobb képzetes hengervetületek paramétereit az alábbi táblázat tartalmazza:
6. táblázat
|
E |
c1 |
c2 |
c3 |
f1 |
y1 |
y2 |
y3 |
|
EAJ=0,30742 |
0,62607 |
-0,14802 |
0,00228 |
0,00275 |
0,99463 |
-0,00760 |
- |
|
EAe=0,68041 |
0,58556 |
-0,04530 |
-0,02719 |
0,00436 |
0,72310 |
0,15376 |
-0,02949 |
|
EAm=0,74199 |
0,69420 |
-0,10078 |
-0,01602 |
0,00423 |
0,98476 |
0,04931 |
-0,01126 |
|
EAK=0,24791 |
0,76042 |
-0,07120 |
-0,02003 |
0,00265 |
1,00182 |
0,00686 |
- |
A parallelkörök mentén az osztásközök a középmeridiántól távolodva kissé növekednek, a határoló meridiánnál mintegy 13–14%-kal nagyobbak, mint a középmeridiánnál. Ez ellentétben van a Baranyi IV. vetületénél tapasztalható osztásköz-csökkenéssel.
Az EAJ kritérium szerinti legjobb pólusvonalas képzetes hengervetület ugyanolyan arányban felosztott parallelkörökkel az 5. ábrán látható.
VI. Legjobb pólusvonalas képzetes hengervetületek
A legjobb képzetes hengervetületeknél megengedjük a parallelkörök tetszõleges arányban való felosztását. Ezek vetületi egyenletét j -ben páros, l -ban páratlan kitevõs polinommal közelítjük:
x=f11× l +f12× l 3+f21× j 2× l +f22× j 2× l 3
Ekkor
![]()
![]()
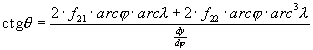
Kiszámítottuk ebben a vetületosztályban is a legkisebb átlagos hibát eredményezõ vetületi együtthatókat
y=arcj , majd elsõ-, harmad- és ötödfokú közelítõ polinom választása esetén. Hasonlítsuk össze itt is az y=arcj (7. táblázat) és y=y1× arcj +y2× arc3j +y3× arc5j (8. táblázat) által szolgáltatott eredményeket az E kritériumok értékei alapján.
7. táblázat
|
E |
f11 |
f12 |
f21 |
f22 |
|
EAJ=0,29278 |
0,56028 |
0,01144 |
-0,06888 |
-0,01042 |
|
EAe=0,69260 |
0,61795 |
0,00990 |
-0,05382 |
-0,00904 |
|
EAm=0,72007 |
0,66028 |
0,00839 |
-0,06557 |
-0,00845 |
|
EAK=0,23601 |
0,72895 |
0,00762 |
-0,00385 |
-0,01316 |
8. táblázat
|
E |
f11 |
f12 |
f21 |
f22 |
y1 |
y2 |
y3 |
|
EAJ=0,29252 |
0,56156 |
0,01137 |
-0,06986 |
-0,01040 |
1,00023 |
-0,01300 |
0,00203 |
|
EAe=0,66236 |
0,56176 |
0,01035 |
-0,04085 |
-0,00890 |
0,76974 |
0,13388 |
-0,02756 |
|
EAm=0,71628 |
0,66252 |
0,00869 |
-0,07059 |
-0,00844 |
0,98863 |
0,04403 |
-0,01108 |
|
EAK=0,23584 |
0,72912 |
0,00766 |
-0,00469 |
-0,01319 |
0,99985 |
0,01052 |
-0,00196 |
Az E értékek az V. vetületosztályhoz képest több %-kal tovább csökkentek. Az EAJ és EAK kritérium-értékek fokszámának növelésével érdemben nem javultak, viszont EAJ és EAK 8.táblázatban szereplõ értékei lényegesen kedvezõbbek, mint a 7. táblázat-beliek. Ezért - hasonlóan a III. osztály vetületeihez - az EAJ és EAK szerinti legjobb képzetes hengervetületet meridiánban hossztartó vetületnek tekintjük.
A 6. ábra mutatja a Föld képét az EAm kritérium szerinti, a 7. ábra az EAK kritérium szerinti legjobb pólusvonalas képzetes hengervetületben. Az egyenlítõ mentén az osztásközök a középmeridiántól távolodva kissé növekszenek, a pólusvonalnál viszont erõsen csökkennek. Hasonló osztásköz-struktúra mutatkozik a többi kritérium szerinti legjobb pólusvonalas képzetes hengervetületeknél is.
Következtetések
A négy különbözõ átlagos teljes torzultsági kritérium (
EAJ , EAe , EAm és EAK) segítségével folytatott vizsgálat eredményei lehetõséget adnak általános következtetések levonására, de a kapott térképek kritériumonként lényeges különbségeket mutatnak. A korábbi vizsgálatok (ld. [4], [5]) eredményeivel egybecsengõen megállapítható, hogy leginkább az EAm és EAK kritérium szerinti legjobb vetületek állnak összhangban a szemlélettel, az esztétikai érzékkel és a hagyományokkal, míg ez legkevésbé az EAJ kritérium szerinti legjobb vetületekre mondható el. Ez is alátámasztja azt a megállapítást, hogy az utóbbi kritérium nagy kiterjedésû területek ábrázolásának torzulási vizsgálatára nem igazán alkalmas.
Az eredmények általánosságban a következõkben foglalhatók össze:
A legjobb pólusvonalas képzetes hengervetületek átlagos teljes torzultsága lényegesen kisebb, mint a valódi hengervetületeké.
A legjobb pólusvonalas képzetes hengervetületek parallelkörei a fentiekben leírt módon változó felosztásúak. Az x vetületi egyenlethez négy együtthatót választva, az optimális vetületeknek kielégítõen pontos közelítését kapjuk.
A legjobb pólusvonalas képzetes hengervetületekre az EAJ és EAK kritérium esetében a meridiánban hossztartó (y=arcj ) változat már elegendõen pontos közelítést ad, viszont elsõsorban az EAe kritériumnál (és kisebb mértékben az EAm kritériumnál) az y fokszámának növelésével az átlagos torzultság még számottevõen csökkenthetõ.
A legjobb pólusvonalas, ekvidisztáns parallelkörû képzetes hengervetületekbõl a szélességek átszámozásával elõnyös torzulású területtartó vetületeket konstruálhatunk.
Mind az ekvidisztáns parallelkörû, mind a változóan felosztott parallelkörû legjobb képzetes hengervetületeknek elsõsorban az EAK , de az EAm (és esetleg az EAe) kritérium szerinti változatai is torzulási szempontból kedvezõbbek, mint a hagyományos képzetes hengervetületek, ezért a teljes Föld ábrázolására hangsúlyozottan javasolhatók.
Irodalom
[1] Airy, G. B.: Explanation of a Projection by Balance of Errors for Maps applying to a very large extent of the Earth's Surface; and Comparison of this projection with other projections. In: Philosophical Magazine and Journal of Science. S. 4. Vol. 22. No. 149. 1861. 409-421.o.
[2] Baranyi J. – Györffy J.: A Föld újszerû ábrázolása a mai magyar atlaszokban. In: Földrajzi Közlemények 3-4/1990. 109-117.o. Budapest.
[3] Bugayevskiy, L. M. – Snyder, J. P.: Map Projections. A Reference Manual. Taylor & Francis, London 1995.
[4] Franula, N.: Die vorteilhaftesten Abbildungen in der Atlaskartographie. Doktori disszertáció, Bonn 1971.
[5] Györffy J.: Anmerkungen zur Frage der besten echten Zylinderabbildungen. In: Kartographische Nachrichten 4/1990. Kirschbaum Verlag, Bonn.
[6] James, H. - Clarke, R. E.: On Projections for Maps applying to a very large extent of the Earth's Surface. In: Philosophical Magazine and Journal of Science. S. 4. Vol. 23. No. 154. 1862. 306-312.o.
[7] 7 " & D " 6 F 8 4 6 ,ñ % .ñ % .:ñ 3 2 $ D " > > Z , ñ H D J * Z ñ ' E I % ; K ,ñ ; @ F 8 & " ñ 1958.
[8] Korn, G. A. – Korn, T. M.: Matematikai kézikönyv mûszakiaknak. Mûszaki Könyvkiadó, Budapest 1975.
[9] Kósa A.: Variációszámítás. Tankönyvkiadó, Budapest 1970.
[10] ; , V , D b 8 @ & , ' . ! .: G , @ D , H 4 R , F 8 4 , @ F > @ & Z < " H , < " H 4 R , F 8 @ 6 8 " D H @ ( D " L 4 4 . = , * D " , ; @ F 8 & " 1968.
[11] Press, W. H. - Teukolsky, S. A. - Vetterling, W. T. - Flannery, B. P.: Numerical Recipes. Cambridge Univ. Press 1986.
[12] Stegena L.: Vetülettan. Tankönyvkiadó, Budapest 1988.
Representing the whole Earth in best pseudocylindrical projections with pole line
Summary
The minimum mean overall error projections were prepared in some groups of pseudocylindrical projections with pole lines. These groups were formed on the grounds of the mapping equation x=x(j ,l ):
In all groups subgroups were formed on the grounds of the mapping equation y=y(j ):
The constituent functions of the mapping equations were approximated by polynomials, and their coefficients giving minimal values of the studied mean overall error criteria (original Airy, Airy-Kavrayskiy, etc.) were computed by the multidimensional downhill simplex method.
The results of the examination:
Összefoglalás
Az átlagos torzultságok szerinti legjobb vetületeket határoztuk meg a pólusvonalas képzetes hengervetületek alábbi csoportjaira, melyeket a vetületi egyenletek alapján alakítottunk ki:
Minden egyes csoporton belül alcsoportokat képeztünk az y=y(j ) vetületi egyenlet alapján:
A vetületi egyenletek alkotó függvényeit polinomokkal közelítettük, és a többváltozós szimplex módszer nevû minimalizáló eljárással határoztuk meg azokat az együttható értékeket, amelyek a
vizsgált átlagos teljes torzultsági hiba-kritériumokra (eredeti Airy, Airy-Kavrajszkij, stb.) a minimális értékeket adták.
A vizsgálatok eredményei:
Ábraaláírások