Lecture notes – Chapter 1
The role of the coordinates and the coordinate systems in the cartography – Introduction
Concept of coordinate(s) and coordinate system
Coordinate(s) – one or more numbers, which identify a definit element of a set of geometrical points, generally by its position.
Coordinate system (in other words reference system, mainly in the geodesy) – a prescription, assigning the coordinate(s) to the element.
Elementary coordinate systems on plane, in space and on surface of revolution
Elementary coordinate systems on the plane:
- planar rectangular (Cartesian) coordinate system
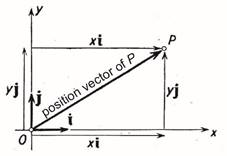
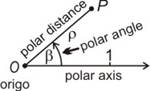
- planar polar coordinate system
Elementary coordinate systems in the space:
- spatial rectangular (Cartesian) coordinate system
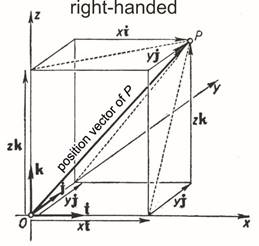
(The axes are arranged „right handed”, if the situation and sequence of the axes corresponds the situation and sequence of the three fingers (thumb, forefinger, middle finger) of the right hand; it is usual in the matematics. In the opposite case, the coordinate system is „left handed” which appears rather in the geodesy.)
- spatial polar (or spherical) coordinate system
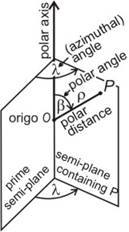
Polar coordinate system on surfaces of revolution
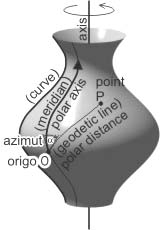
The draft of the cartographical representation of the Earth surface
In the cartography a three-dimensional figure – the Earth’s surface with its objects – will be represented in two-dimensional space – on the plane (on paper or on a screen). To the localization of the points of these objects to be represented, their coordinates must be known either on the Earth’s surface, or on the plane. The connection between the coordinates of two kinds – a mapping („map projection”)– comes true by the so called „projection equations”.
Expected properties for the two surfaces:
- continuous
- regular
- describable by formulas or series
Expected properties for the mapping between the two surfaces:
- twice continuously differentiable
- injective
- describable by formulas or series
Substitution of the physical Earth’s surface by an approximate one, satisfying the conditions
The Earth’s irregular surface as geographical relief (with elevation) will be projected onto the geoid, disregarding the elevation
Geoid:
- let the gravitational equipotential surfaces (where magnitude of force of gravity is the same) be considered; the direction of the gravitational vector, the „local vertical” traced out by the plumb line is everywhere perpendicular to these surfaces
- chosen one from these surfaces, which coincides the mean sea level supposed being at rest, and extended it to the area of continents in imagination
-
it is irregular surface, too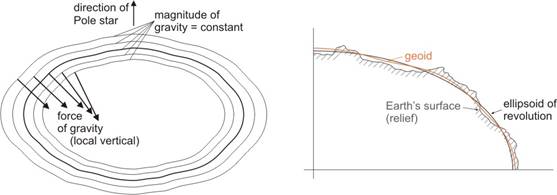
The representation of the Earth’s surface and its objects, projected onto the geoid needs a regular, describable by formulas (or series) and continuous approximating geometrical shape. Options, depending on the accuracy of the representation (with its well-known equation in the spatial rectangular coordinate system):
Plane (area < 10 km2) 
Sphere (scale of mapping < ~ 1 : 1 million) 
Ellipsoid of revolution (spheroid) – hereafter ellipsoid (a surface of revolution obtained by rotating an ellipse about its shorter axis)
Sketch of the representation of the globe surface on maps:
1. abstraction step: 2. abstraction step: mapping („map projection”):
Earth’s surface ® geoid geoid ® ellipsoid (or sphere) ellipsoid (or sphere) ® plane
(irregular) (irregular) (irregular) (regular) (regular) (regular)
Main properties of an ellipsoid of revolution
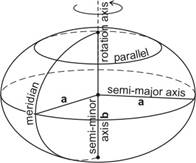
a – semi-major axis, radius of the Equator
b - semi-minor axis
f – flattening 
or 1/f
– inverse flattening
e – first eccentricity 
(there
is often used its square e2, too)
e’ – second eccentricity 
and its sqare (e’)2
Generally a and 1/f are given; then e2 and b can be calculated:
and
For example WGS’84 ellipsoid:
a = 6 378 137.0 m
1/f = 298.257 223 563
e2 = 0.006 694 379 990 14
e = 0.081 819 190 9
b = 6 356 752.31 m
e’ = 0.082 094 438 06
Other ellipsoids in use: e.g., Bessel, Clarke 1880, Hayford, etc.