Lecture notes – Chapter 6
Azimuthal coordinate systems
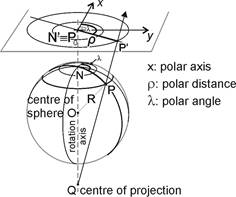
Let a mapping be established by projecting the points of a spherical surface from a centre onto a plane by straight lines – „projectors” (central perspective projection). The presribed reflection symmetry of the map graticule requires the centre to be on the rotation axis of the Earth sphere, and the plane to be perpendicular to the axis.
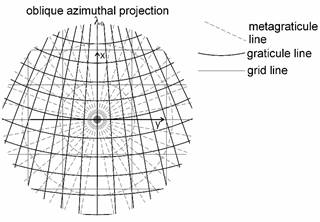
Then the map graticule is composed of concentric circles and straight lines crossing the common center of the circles. Generalizing these properties of the map graticule, the azimuthal projections can be defined by their graticule or metagraticule with the following requirements:
- the images of the parallels are concentric circles, the common center is the image of the pole
- the images of the meridians are straight lines, crossing the common center of the circles above
- the images of the parallels and meridians are perpendicular
- the angles included by the meridians are equal to the angles of their images (property of azimuthality)
they are called normal (polar) version;
or (in case of a spherical reference surface) there exists a metacoordinate system, where the above mentioned properties are valid for the metagraticule, and they are called transverse (equatorial) or oblique version depending on the location of the metapole.
It is practical to take a polar coordinate system, whose origin is in the common center of the parallels (or the metaparallels) and the polar axis coinciding the midmeridian l0 (or the prime metameridian). So the polar distance of a map point is a strictly decreasing function r (the radius of the mapped parallel) depending on the latitude j (or on the metalatitude j*), and the polar angle equalled the longitude difference l-l0 (or the metalongitude l*). The property of r(j=90°)=0 is required in the normal version, and r(j*=90°)=0 in other cases, too, which guarantee the common center of the parallels (or metaparallels) to be the image of the pole (or the metapole). The rectangular coordinates of the normal version of an azimuthal projection can be got from the next formulae:
![]()
![]()
or in case of transverse or oblique version
![]()
![]()
The graticule distortions in the normal version are:
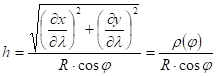
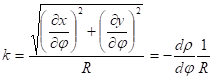
and
![]()
due to the orthogonality of the graticule.
Similarly the azimuthal projections of the ellipsoid is expressed by
![]()
![]()
(L0 is the midmeridian on the ellipsoid.)
The graticule distortions are in this case:
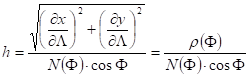
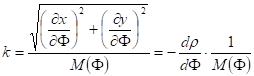
Stereographic projection of the sphere
The centre Q of the projection coincides with one of the poles, and the map plane is mostly tangent to the sphere of radius R at the other pole.
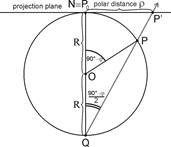
As the measure of inscribed angle is always half the measure of the central angle belonging to the same circular arc („central angle theorem”), the polar distance r is:
![]() .
.
It can be altered by trigonometric identities:
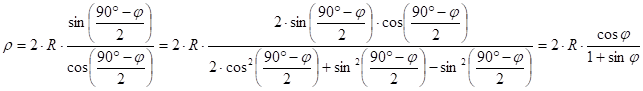 In this way
the projection equations are:
In this way
the projection equations are:
![]()
![]()
The scale distortions along the parallels:
![]()
The scale distortions along the meridians:
![]()
![]()
As the map graticule is rectangular, the equality h=k means that the projection is conformal. The linear scale l in an arbitrary direction is equal to h and k, and the area scale p is equal to h×k. Their value depends only on the latitude, so they are constant along the parallel circles, and are continuously growing if the point moves away from the pole. Specifically h=k=1 comes true in case of j=90° which means that there are no scale or area distortions at the pole locally, and they are negligible in the neighborhood of the pole. This projection provides advantageous distortion conditions for the conformal representation of a circular area about the pole.
Sometimes the map plane perpendicular to the rotation axis cuts the spherical surface, and the intersection line is a true scale parallel circle. This position means a scaling down of the map plane and results in proportionally reduced map distances as well as map coordinates. In this case the true scale parallel is without any area distortion, and there are slight length and area reductions within it.
The geocartography prefers the application of stereographic projection for representing the polar area because of its conformality and other favourable distortion properties.
Oblique stereographic projection of the sphere
If the favourable cartographical properties of the stereographic projection are needed on maps representing territories far from the pole, an oblique stereographic projection can also be applied with the metapole in the centre of the area to be represented.
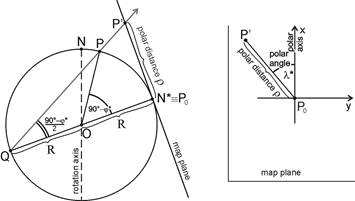
In this case the projection equations above are referred to the metacoordinates:
![]()
![]()
The calculation of the map coordinates x, y from the geographic coordinates j, l is carried out by using the transformation formulae between the geographic coordinates and metacoordinates j*, l*.
There are explicit formulae for calculating the coordinates of the oblique stereographic projections. Let the following formulae, derived from the cosine rule for sides, the law of sines and the cotangent four-part formula be substituted into the projection equations above one by one:
![]()
![]()
![]()
Each of them was set up in the polar spherical triangle NN*P, where j0, l0 are the geographical coordinates of the metapole N*.
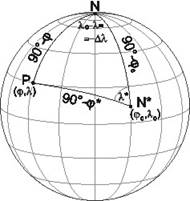
Then the projection equations for the oblique stereographic projection will be got:
![]()
![]()
If the map coordinates x, y was measured or they are given in a coordinate list, and the geographic coordinates j, l are asked, then the starting-point for the reverse projection equations is the square root of the sum of squared map coordinates:
![]()
Hence
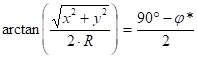
finally

and
![]()
The explicit inverse equations which can be obtained from trigonometric calculations, are:
![]()
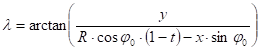
where
![]()
The circles on the sphere that do not pass through the centre of the projection, are projected generally onto circles on the map plane (or, exceptionally, onto straight lines), therefore both the images of the paralells and meridians appear on the map as circular arcs.
This projection is in use mainly in the geocartography, for representing roughly round-shaped areas.
Other perspective azimuthal projections of the sphere
- Orthographic (orthogonal) projection – aphylactic, parallels are true scale
- Gnomonic (central) projecton – aphylactic, great circles are mapped onto straight lines
Other non-perspective azimuthal projections
- Lambert azimuthal projection – equal-area
- Postel azimuthal projection – meridians are true scale
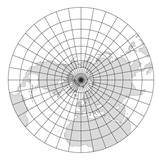
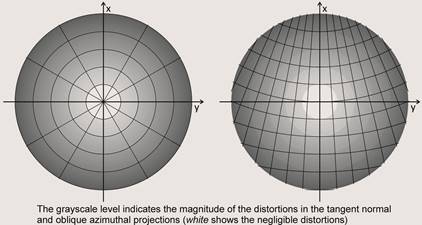
The distribution of the distortions in a normal and oblique azimutal projections can be seen in the following figure:
Conformal azimuthal („stereographic”) projection of the ellipsoid
This projection is conformal, but – contrary to the spherical version and its name – not perspective, that is, it can not be established by projectors starting from a centre point. The equation of the conformality (respecting the rectangular graticule): h=k, which is in this case
![]()
The solution of the equation, taken into consideration the evident requirement r (F=90°)=0, is:
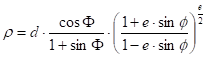
This projection named Universe Polar Stereographic (UPS) is used for the topographic maps of the polar area completing the World map system UTM. In case of WGS84 ellipsoid d=12 637 318.50 m, and the true scale parallel on the WGS84 ellipsoid is: Fn=±81° 6’52.2648”. The origin is shifted from the pole 2000 km to west (false easting) and 2000 km to south (false northing). The navigation maps called World Aeronautical Chart (scale 1:1 million) for the polar area use a similar projection on the Hayford 1924 ellipsoid with d=12 621 895.458 m and the true scale parallel Fn=±80°14’19”.
Conformal mapping of the ellipsoid by „double stereographic projection”
A representation of the ellipsoid can be established by inserting an aposphere amongst the ellipsoid and map plane, and combining two conformal mappings: a transformation from the ellipsoid to an aposphere, and an oblique stereographic projection from the aposphere to the plane. It is the so called „double stereographic projection”.
The equations created by Thomas:
![]()
![]()
where k0 is the linear scale in the central point F0,L 0. The formula giving the spherical latitude j from the ellipsoidal latitude F:
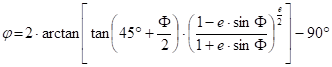
The usual inverse formulae starting from the rectangular map coordinates x,y:
![]()
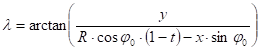
where
![]()
can be applied with the substitution of
![]()
and the spherical longitude l is considered as the ellipsoidal L, while the ellipsoidal latitude can be calculated by iteration using the formula given in the subsection ”Conformal projection of the ellipsoid onto the sphere”:
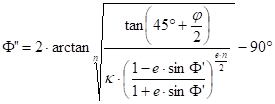 then
then ![]() until
until
![]()
where e is the required accuracy of the calculation; finally F=F”. A possible initial value: F’=j The values for the parameters are chosen as n=1 and k=1.
The cadastral maps in the Habsburg Monarchy in the 19th century used the predecessor of this projection, applying reverse (x oriented to South and y to West) coordinate system. In this version the parameters of the mapping from the Bessel ellipsoid to the aposphere with minimal scale distortion were calculated by the Gauss’s formulae, whilst the true scale parallel of the mapping differed from the latitude of the metapole of the oblique stereographic projection. A similar double stereographic projection with the Schreiber mapping was chosen for the topographic map system of Netherlands.
Roussilhe produced a conformal projection by power series expansion of a mapping which assigns azimuthal straight lines on the plane to the geodesic lines starting from a middle point of the area to be represented on the ellipsoid. This projection was adapted by the Bulgarian geodesist Hristow to the territory of Romania (projection Stereo70 on the Krasovsky ellipsoid) that is still in use today. Topographic map system GUGIK80 in the same projection with other correspondent coefficients was established in Poland.