Lecture 11A

Cylindrical map projections

Cylindrical map projections in general

Let a mapping be taken which is generated by a central perspective projection from a spherical surface onto a superficies of a cylinder of revolution. In order to the reflection symmetry of the map graticule, the centre has to be on the common rotation axis of the Earth sphere and the cylinder.

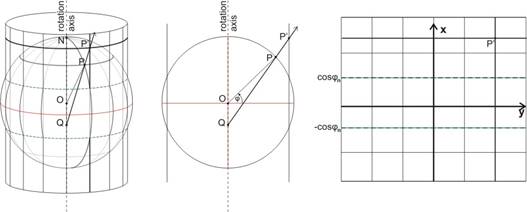
Then the projectors belonging to the points of a parallel generate a superficies of a cone of revolution, and the projectors belonging to the points of a meridian generate a plane including the rotation axis. Their intersection lines on the cylindrical superficies create circles and straight lines (the latter coincide with the „generators” of the superficies), which become a planar rectangular grid as the map graticule after unfolding the superficies into a flat surface. Generalizing these properties of the map graticule, the cylindrical projections can be defined by their graticule or metagraticule, requiring that

- the images of the parallels are parallel straight lines

- the images of the meridians are parallel straight lines

- the images of the parallels and the meridians are perpendicular

- the distance Dy between the meridians is proportional to the correspondent longitude difference Dl

- the map graticule has in general two axes of reflection symmetry: the midmeridian (or the prime meridian) and the Equator

they are called normal (polar) version;

or (in case of a spherical reference surface) there exists a metacoordinate system, where the above mentioned properties are valid for the metagraticule, and they are called oblique or transverse (equatorial) version of a cylindrical projection depending on the location of the metapole.

Because of the properties of the map graticule, the rectangular coordinates of the normal version are the following:

where the strictly increasing function  x(j)  is an odd one, and the coefficient  c  depends on the latitude  j_s  of the true scale parallel (in other words the „standard parallel”), in the practice:  c=cosj_s.

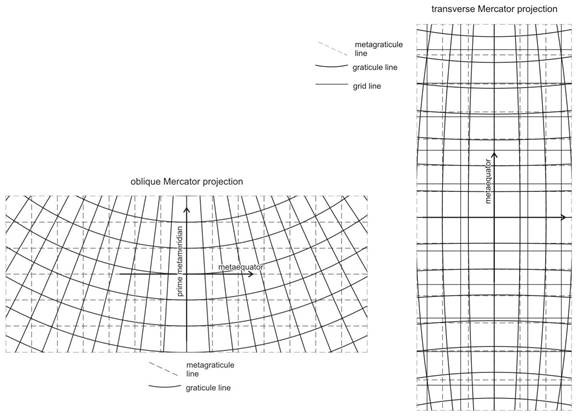
In the case of transverse or oblique version:

where  c=cosj_s* (j_s*  is the true scale metaparallel).

The graticule distortions are:

and

because of the orthogonality of the graticule.

Similarly, the cylindrical projections of the ellipsoid can be given by

 (L₀ is the midmeridian on the ellipsoid, x(F) is a strictly increasing and odd function, furthermore F_s is the latitude of the true scale parallel.) The graticule distortions are:

Both the spherical and ellipsoidal cylindrical projections have favourable distortions in the surroundings of the Equator. This area is wider, if there are two true scale parallels  ±j_s (or F_s , respectively) and it is narrower in the case of a true scale Equator (j_s =0°, or F_s=0, respectively). They are used mainly for maps representing the neighbourhood of the Equator, or at least an area symmetric with respect to the Equator.

Conformal cylindrical projection of the sphere (Mercator’s projection)

The equation of the conformality (respecting the rectangular graticule):  h=k, which is in this case

Integrating the equation, the function  x  will be got:

(The constant of integration equals  0  because of the evident requirement  x(j=0°)=0.)

This formula can be transformed by the next identity:

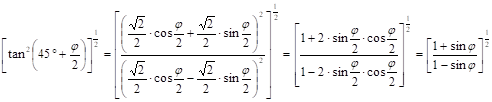
Hence the other version of the Mercator’s projection equation  x  is:

while

as usual by the cyindrical projections.

The inverse projection equations can be obtained by expressing the geographic coordinates:

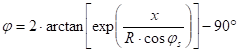
A loxodrome is a line on the surface of the sphere, which has the same azimuth  a  in its every point (a=constant). Thus the meridians  (a=0°) and the parallels (a=90°) are trivial loxodromes. The loxodromes with a differing azimuth are spherical spirals leading from one pole to the other. If the path of a ship or an aeroplane maintains a fixed compass direction during the travel, it moves along a loxodrome.

If a loxodrome has the azimuth  a  and crosses the spherical point P₀ (j₀,l₀), then its equation is:

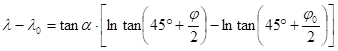
Multiplying it by  R×cosj_s with an arbitrary latitude of  j_s:and applying the projection equations  x  and  y  above,  the formula

will be got which is an equation of a straight line crossing the map point P₀’(x₀,y₀) assigned to the Earth point  P₀(j₀,l₀). This straight line and the vertical axis  x  include an angle  a.  It proves that the spherical loxodromes are represented by straight lines on those charts which were mapped by the Mercator’s projection. Therefore the shipping on the oceans which preferred the pathes along loxodromes from the XVII century, used Mercator’s maps to the navigation.

Cylindrical equidistant projection of the sphere

The true scale meridians are equivalent to the equation  k=1, that is

so the projection equation  x  is:

This projection is neither conformal, nor equal-area, so it is an aphylactic projection. In case of a true scale Equator its name is „plate carrée”. Sometimes it is used with true scale parallel(s) differing from the Equator, too.

Other notable cylindrical projections

· Lambert’s equal-area cylindrical projection

· Central perspective cylindrical projection (the projectors start from the centre of the sphere; aphylactic)

Conformal cylindrical projection of the ellipsoid

Due to the rectangular graticule, the equation of the conformality:  h=k, which means the following equation:

that is

After integrating:

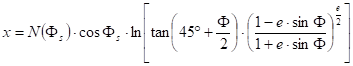
(By the constant of integration the requirement  x(F=0°)=0 was taken into consideration.)

It can be used advantageously for large scale maps representing the surroundings of the Equator.

Cylindrical projection of the ellipsoid with true scale meridians

Similarly to the spherical version, the true scale meridians can be formulated by the equation  k=1, that is

which is equivalent to the projection equation

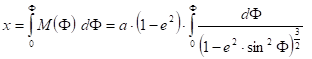
and

This projection is neither conformal nor equal-area hence aphylactic.

An equal-area cylindrical projection can be constructed, too.