Lecture 11B

Oblique cylindrical map projections

The distribution of the distortions in the oblique map projections

The distortions arising on the map, increase with the distance from the metaequator while they are negligible near the metaequator.

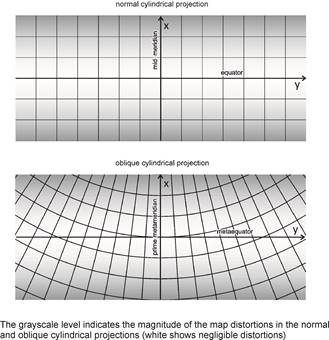
Oblique conformal cylindrical projection (oblique Mercator)

If the area to be represented expands along a great circle of a sphere, then taking this great circle as the metaequator of a metacoordinate system, a conformal cylindrical projection should be referred to the metacoordinates j*, l*:

Using the metacoordinate transformations

and the formula for  tanl*  which is usual instead of the  sinl*  originating in the law of sines:               

which derives from the law of sines and the cosine rule for sides.

The projection equations are:

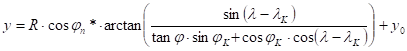
where  j_n*  is the true scale metaparallel, and  P_K (j_K,l_K)  is the intersection of the metaequator and the prime metameridian, furthermore  x₀,y₀  are the planar translation coordinates of the origin („false northing”, „false easting”). The angle issuing from the expression „arctan” has to be taken in radian measure.

The inverse coordinate can be calculated by the trivial reverse use of the projection equations, and after it by the transformation of the metacoordinates into geographical coordinates:

x,y ® j*,l* ® j,l

The straight equations derived from trigonometry are:

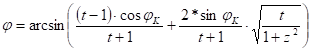
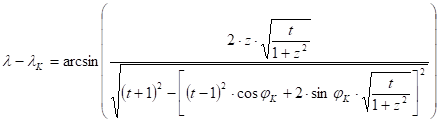
where

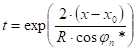                  and                       

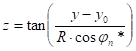
A representation on the ellipsoid can be generated by a combination of two mappings (one of them is a conformal mapping from the ellipsoid to an aposphere, and the other one is an oblique conformal cylindrical projection from the aposphere to the plane). This „double Mercator projection” was constructed by Rosenmund in 1903 for the representation of Switzerland (Swiss Oblique Mercator). The same projection was adapted for the cadastral mapping of Hungary by Fasching in 1909 with three different cylinders. About 1970 it was modified by taking only one cylinder and a reduction factor of 0.99993 („EOV” projection).

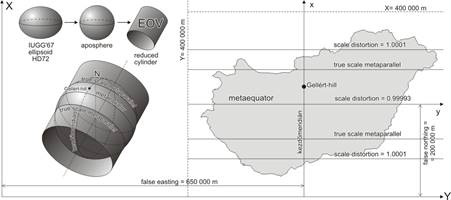
Laborde used a similar projection for the topographic mapping of Madagascar in 1928.

Hotine oblique Mercator projection

This conformal mapping assigns a true scale straight line („initial line”) of the map to an ellipsoidal geodetic line („centre line”). Given the ellipsoidal parameters (semi-major axis  a  end first eccentricity  e), the centre of the projection F_C,L _C located on the centre line,  the azimuth a_C  of the centre line taken in the centre of projection, and lastly the scale distortion k_C at the centre of projection.

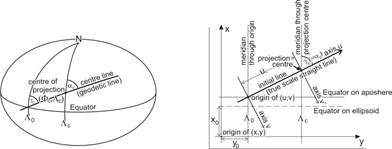
Asked the u,v planar coordinates in a rectangular coordinate system whose origin is placed on the initial line, and the axis u coincides with it. The constants which are required to calculate the position coordinates u_C,v_C of the origin:

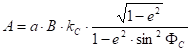
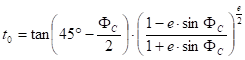
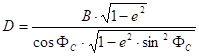
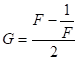
, or in case of a_C =90°:     

and (taking the origin at the intersection of the initial line and the image line of the aposphere’s Equator):

or (taking the origin at the image of the centre point at the initial line):

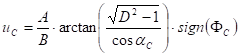,   or in case of a_C =90°:      

and of course

Giving the geographical coordinates F,L  of the point in question, we obtain the rectangular coordinates  u,v:

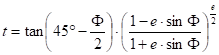
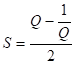
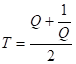
and finally

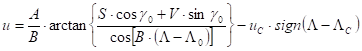
The image of the meridian L _C  is a straight line on the map. If the axis x of the target coordinate system is parallel to it, then the u,v coordinates are additionally rotated by  g_C (which equals  a_C  due to the conformality), and translated by x₀,y₀, so the formulae are:

Thus the map coordinates can be directly calculated from the ellipsoidal geographic coordinates, because the data refering to the intermediate aposphere don’t appear in the formulae.

This projection can be adapted for a sufficiently accurate approximation of the Swiss Oblique Mercator and the Hungarian EOV projections with  a_C =90°.