Lecture 11C
Transverse cylindrical map projections
Transverse cylindrical projections of the sphere
In the transverse case, the metapole is situated on the Equator, consequently the metaequator coincides with a meridian denoted by lK which is placed in general in the middle of the area to be represented, mostly a spherical lune bounded by two meridians.
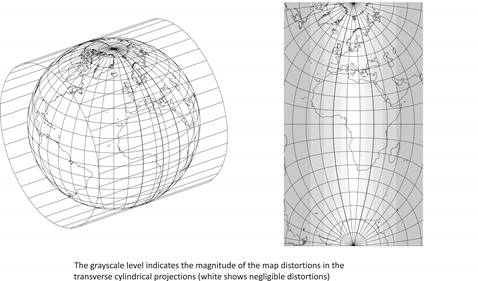
This midmeridian lK and the Equator are mapped onto straight lines perpendicular to each other, which are the axes of symmetry of the graticule, so they can provide the coordinate axes. These projections are usually applied for mapping long and relatively narrow areas lying along a meridian, where they show favourable distortions. Either two appointed metaparallels ±j*s or the metaequator (j*s=0°) can be true scale depending on the width of the area to be represented.
The projection equations are referred to the metacoordinates j*, l* which can be received from the formulae
![]()
and
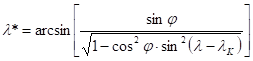
Thus the mapping functions of the transverse conformal cylindrical (frequently „transverse Mercator”) projection are the following:
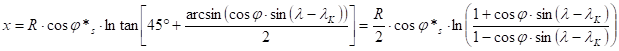
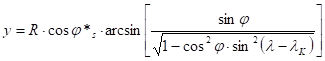
where ±js are the metalatitudes of the true scale metaparallels. (The angle arising from the arcsin in the formula of y has to be taken in radian measure.)
The transverse equivalent cylindrical projection (namely Cassini projection) has to be mentioned, too. Its mapping functions are:
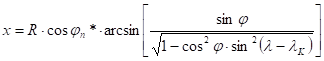
![]()
Both projections, but mainly the latter aphylactic one, are used for mapping of spherical lunes to paper „gores” for the globe making.
Transverse Mercator projections of the ellipsoid
The application of a double projection wouldn’t be advantageous due to the greater distortions of the conformal mapping from the ellipsoid to the sphere on the areas far from the true scale parallels. Therefore the direct mapping of an ellipsoidal lune to the plane (figure) comes true by a complex function which maps the midmeridian LK of the lune to a true scale straight line. After the power series expansion of the complex function with respect to (L-LK) and separating it into a real and an imaginary part, we obtain the eqations of the Gauss-Krüger projection:
![]()
![]()
where
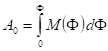
that is the arc length of the meridian between the Equator and the latitude F which can be calculated numerically, or approximated by the following series:
![]()
![]()
(where in case of Krasovskiy S-42 ellipsod, the reqired data above are: a=6 378 245.0 m and e2=0.0066934275)
and ![]() (i=1,2,3,…).
(i=1,2,3,…).
Hence
![]()
![]()
![]()
![]()
![]()
![]() ,
,
where
![]() .
.
Conversely, the ellipsoidal geographic coordinates F, L can be obtained from the coordinates XGK, YGK as follows. Our starting point is the intersection T of the midmeridian LK and the straight line which crosses the point XGK, YGK furthemore perpendicular to the midmeridian. Let the latitude of the point T denoted by FT . It can be got from the solution of the nonlinear equation
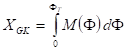
or from the series
![]()
where
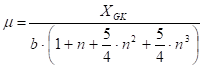
and
![]()
(b=6 356 863.0 m is valid for the Krasovskiy S-42 ellipsoid).
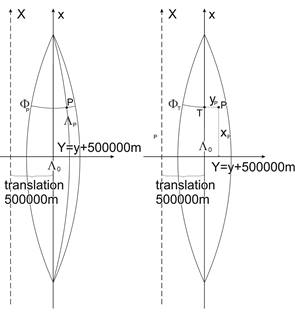
The geographic coordinates issue from the inverse equations
![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
![]()
![]()
and
![]() .
.
The midmeridian LK is free of distortions. Moving away from it, the scale and area distortions, namely the linear scale and the area scale increase.
Gauss-Krüger grid system
The Krasovskiy S-42 ellipsoid is partitioned into 60 congruent parts – „zones” – along meridians. All these ellipsoidal lunes with a longitude difference of 6° are mapped by the same Gauss-Krüger projection to a zone so, that the images of the midmeridians and the Equator – straight lines – are the axes of symmetry of the zones. The zones are numbered starting from the Date Line eastwards from 1 to 60. Their axis y coincides with the Equator, and the axis x on the map is translated from the midmeridian to the West by 500000m (false easting), that none of the coordinates y in the zone are negative.
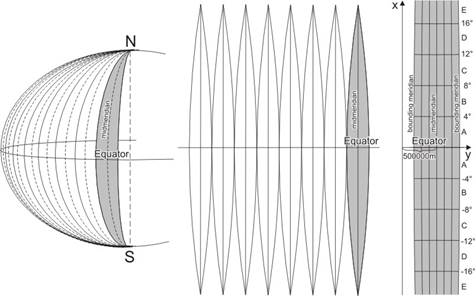
The integer part of the coordinate number x (rounded to meter) consists generally of 7 digits. The same of the coordinate number y is composed of only 6 digits, and before them stands the second digit of the serial number of the zone („leading number”). It has not to be taken into consideration in the coordinate calculations, but it gives some information about the location of the point in question on the Earth.
Every zones of 6° are partitioned by parallels into geographic quadrangles with a latitude difference of 4°. They are denoted by letters of the English alphabet using them from A to V starting from the Equator both to north (N) and to south (S). A 1:1 000 000 map sheet represents an area of 6°x4°.
Inside a zone of 6°, the midmeridian is free of distortions; the linear scales l are maximal at the intersection of the Equator and the bounding meridians (lmax»1.0013), therefore lunes of 2° (lmax»1.00015) and 3° (lmax»1.00034) are usual in some countries mostly on Bessel ellipsoid for geodesic purposes.
Universe Transverse Mercator (UTM) projection
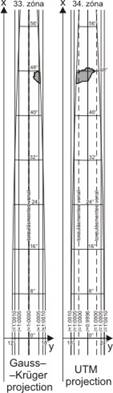
The UTM projection is the modification of the Gauss-Krüger projection with a reducing factor of 0.9996 in order to diminish the maximal scale and area distortions. Instead of x and y the UTM coordinates are denoted recently by „UTM Northing” and „UTM Easting” as usual. Assuming that both GK and UTM projections use the same ellipsoid and if the false easting of 500000m is taken into consideration for both projections then the projection equations can be written in the following form:
![]()
![]()
Similarly the inverse projection equations can be obtained from the same of the Gauss-Krüger projection by the following formulae:
![]()
![]()
The UTM grid system
The basic (earlier the Hayford, in the last decades the WGS84) Earth ellipsoid’s area between the 80th parallel south and the 84th parallel north is partitioned by meridians into congruent lunes (so called zones) whose longitude difference is 6°. The integer part of the coordinate number x consists of 7 digits, and the same of the coordinate number y includes 6 digits. The false easting of 500000m results in positive y coordinates.
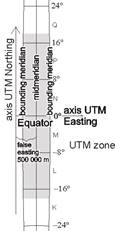
Every 60 zones between the 80th parallel south to the 84th parallel north are partitioned by parallels into geographic quadrangles with a latitude difference of 8°, but the last one between 72° and 84° of north has 12° difference. They are denoted by letters of the English alphabet using them from C to X (except for I and O) starting from south to north. Four sheets of 1:1 000 000 map represent an area of 6°x8°. The Antarctic Region to the 80th parallel south is represented in UPS (Universe Polar Stereographic) projection, and its western and eastern half parts are denoted by A and B. The Arctic Region from the 84th parallel is represented in UPS, too, and its eastern and western half parts are denoted by Y and Z.
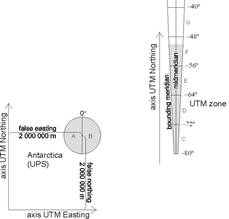
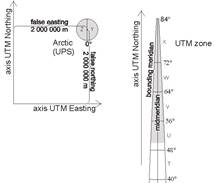
The distribution of the scale and area distortions inside a zone of 6° is determined by the scaling factor 0.9996, which provides the linear scale along the midmeridian. There are two true scale straight lines parallel with the midmeridian. (Their intersections on the Equator have ±1°37’15.2” longitude difference from the midmeridian intersection.) The arc length and the area decrease between the true scale straight lines, while they increase outside them. The linear scale along the midmeridian equals 0.9996, and its value is maximum (»1.00097) at the intersection of the Equator and the bounding meridians.
Cassini-Soldner projection
Let an ellipsoidal lune – a „zone” – be mapped onto the map plane with a true scale midmeridian in such a way that the images of the geodesic lines (orthodromes) perpendicular to the midmeridian would turn into true scale straight lines perpendicular to the image of the midmeridian. Thus the images of these ortodromes become parallel lines on the map plane. Let the midmeridian and the Equator on the map as perpendicular straight lines be chosen as the x and y axes of the rectangular coordinate system. This is the so called Cassini-Soldner projection which is the ellipsoidal generalization of the transverse equivalent cylindrical projection (in other words the Cassini projection).
The projection equations are the following:
![]()
![]()
This projection is aphylactic that is neither conformal nor equal area, and the distortions are small in the neigbourhood of the midmeridian therefore it was used for topographic maps in the XVIII – XX centuries in some countries (France, Bavaria, the Habsburg Monarchy, Great Britain, Italy, Norway, Russia, Israel).