Conical map projections
Modelled on the azimuthal and cylindrical projections, let a mapping be taken which results in a central perspective projection from a spherical surface onto a superficies of a cone of revolution. In order to symmetry of the map graticule, the centre has to be on the common rotation axis of the Earth sphere and the cone. Then the projectors belonging to the points of a parallel, create a superficies of a cone of revolution, and the projectors belonging to a meridian generate a semi-plane bounded by the rotation axis. Their intersection lines on the conical superficies create circles and straight lines (the latter coincide with the generators of the superficies). After the unfolding the conical superficies, which becomes a circular sector, the cutting circles become concentric circular arcs and the generators become straight lines crossing the common centre.
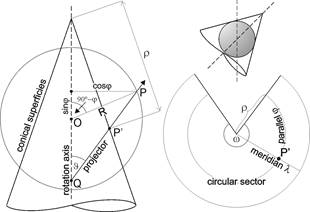
If the conical superficies is tangent to the sphere then the tangent line (a circle) is the single true scale parallel; in case of cutting superficies, the cutting curves are the two true scale parallels.
Generalizing these properties of the map graticule, the conical projections can be defined by their graticule or metagraticule, requiring that
- the images of the parallels are concentric circular arcs
- the images of the meridians are straight lines, converging towards the common center
- the images of the parallels and the meridians are perpendicular to one another
- the angles included by the meridians are proportional to the angles of their images, and the reciprocal of this proportion, called constant of the cone or convergency factor, equals the ratio of the central angle w of the circular sector and the full angle
they are called normal (polar) version;
or (in case of spherical Earth) there exists a metacoordinate system, where the above mentioned properties are valid for the metagraticule, and they are called oblique or transverse (equatorial) version depending on the location of the metapole. In the practice the conical projections used to have one or two true scale parallels.
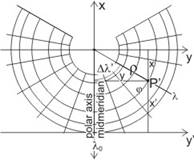
On the projection plane, the points of the circular sector in question can be localized advantageously by a polar coordinate system having the origin in the common centre of the images of the parallels and the polar axis on the image of the midmeridian l0. The polar distance r is the radius of the parallel on the map, and the polar angle Dl’=(l’-l0’) gives the angle between the meridians on the map. The relationship of Dl’ and the longitude difference Dl=l-l0 between the correspondent meridians is, because of the property of proportionality mentioned above:
![]()
where the constant n of the cone
![]()
is the constant of the angular proportion (w is the central angle of the circular sector).
The origin of the rectangular and the polar coordinate systems coincide, and the the negative part of axis x coincides with the polar axis. The axis y sometimes can be shifted to avoid the negative x coordinates.
Hence the rectangular coordinates of the normal version:
![]()
![]()
or in case of transverse or oblique version
![]()
![]()
The graticule distortions are:
![]()
![]()
and
![]()
due to the orthogonality of the graticule.
Similarly, the conical projections of the ellipsoid is described by
![]()
![]()
(L0 is the midmeridian on the ellipsoid.)
The graticule distortions are in this case:
![]()
![]()
Lambert conformal conical projection of the sphere
The equation of the conformality: h=k, which means that
![]()
After integration of the separable equation:
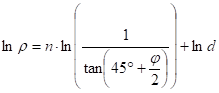
where d is the constant of integration. Then the radius r of the parallel j on the map:
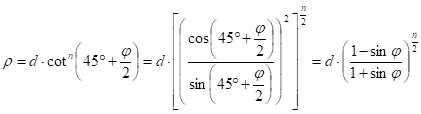
where the parameters d and n can be obtained from the location of the true scale parallel(s). Thus in the case of one true scale parallel js , the equations
![]()
and
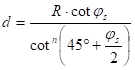
give them.
Other notable conical projections of the sphere
- Lambert’s pointed-polar equal-area projection (one true scale parallel)
- Albers curved-polar equal-area projection (two true scale parallels)
- Equidistant conical projection (the meridians and one parallel are true scale, aphylactic)
- De l’Isle equidistant conical projection (the meridians and two parallels are true scale, aphylactic)
Lambert conformal conical projection of the ellipsoid
Similarly to the spherical version, the equation of the conformality is h=k, which is in this case
![]()
Its solution is:
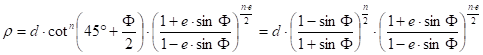
where the values of the parameters n and d depend on the location of the true scale parallel(s). In the case of one true scale parallel Fs the equations
![]()
and
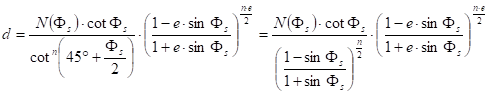
are realized.
Supposing that F1 and F2 are the true scale parallels, the following formulae give the parameters d and n:
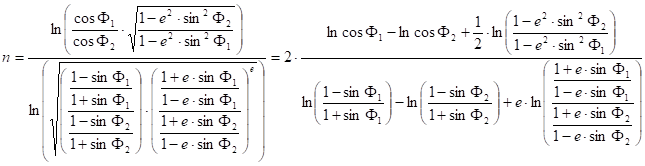
and
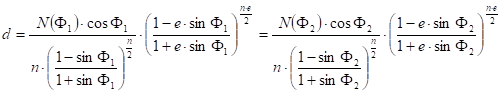
On occasion, this is called Lambert-Gauss projection.
An advantageous property of the conformal conical projection is that the Earth’s orthodromes (geodesic lines) not longer than 3000 km hardly deviate on the map from the straight lines.
The World map system „World Aeronautical Chart” (WAC, scale 1 : 1 000 000) of the International Civil Aviation Organization (ICAO) has been used this projection since 1962. (It replaced the UTM projection.) The sheet division of this map system is like the same of the Gauss-Krüger topographic World map system. Between the 60th parallel south and the 60th parallel north, the ellipsoid is partitioned into zones of 6° and bands of 4°, so this territory is represented on geographic quadrangles of 6°´4°. Outside of the parallels ±60°, the longitude difference of a geographic quadrangle is greater because of the contraction of more zones. This map system contains maps of larger scale (1 : 500 000), too, whose sheet system flexibly adapts to the location of important air transport centres. The surroundings of the poles are represented in the earlier mentioned polar stereographic projection.
The true scale parallels F1 and F2 of the map sheet representing a territory of 6°´4°, are 40’ to the north of the southern bounding parallel and 40’ to the south of the northern bounding parallel. In the practical use, the constant of the cone n is approximated by the same of a similar map sheet of one true scale parallel whose latitude Fs resultes in by averaging the original true scale latitudes F1 and F2.
The projection of maps displaying the images of meteorological satellites is the Lambert conformal. The topographic mapping of France, Belgien and some countries in northern Africa (Morocco, Algeria, Tunisia, Egypt) comes off in this projection, too.
Oblique conformal conical map projection on the sphere
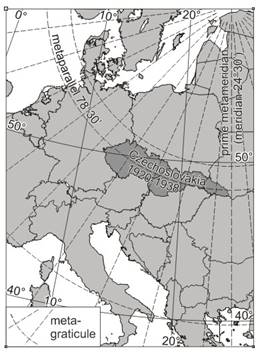
This version is advantageous for representing areas expanding along a small circle of a sphere. Then taking this small circle as the metaparallel of a metacoordinate system with j0, l0 as the metapole, a conformal conical projection should be referred to the metacoordinates j*, l*, where
![]()
and
![]()
The Krovák projection established in Czechoslovakia for the surveying and topographic mapping between the World Wars. This double projection was composed of a conformal mapping (with the true scale parallel of Fs=49°30’) from the S_JTSK geodetic datum (based on Bessel ellipsoid) to an aposphere, and an oblique conformal conical projection of the aposphere to the plane. The coordinates of the metapole are:
F0=59°45’27”
L0=24°50’ (Greenwich)
The metaparallel with scale distortion 0.9999 is given:
js*=78°30’
The meridian of 24°30’ coincide with a metameridian, so its image – a straight line – can be parallel to the axis of the planar rectangular coordinate system.