Lecture notes – Chapter 4

Geodetic datum and substituting sphere

Fitting the ellipsoid to the geoid

The astronomical coordinates of a point on Earth’s surface are, aside from the measurement errors, unambiguously defined on the geoid. The ellipsoidal geographic coordinates of the same point depend on the position of the ellipsoid related to the geoid. For their unambiguity, an assignment between the coordinates of two types is needed. To realize it, the ellipsoid has to be fitted to the geoid. The coordinates of some selected triangulation stations, the so called Laplace points have been fixed both by astronomical and Earth-based survey measurements  (the latters refer to an ellipsoid). After the adjustment calculations and the reduction to the geoid, the ellipsoid will be determined by the minimisation of the sum of the squared angle differences between the vertical directions on the geoid and the ellipsoid („plumb-line deviation” or „deflection of the vertical”) in the Laplace points. This fitted ellipsoid is called the geodetic datum (or simply datum).

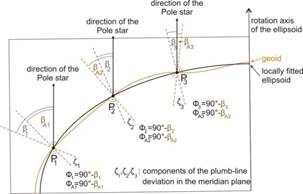
The surface of this ellipsoid and the geoid surface are approximately parallel in the environment of the Laplace points, so a locally fitted ellipsoid (e.g., SAD69 in Brazil, Schwarzeck in Namibia, Indian Geodetic Datum in India, Krassovsky 1940 in Kazakhstan, NAD83 in the USA, Carthage in Tunisia, European Datum 1950 in Turkey, HD72 in Hungary) will be created. The satellite geodesy enables to establish globally fitted ellipsoid, too (e.g., WGS84 datum).

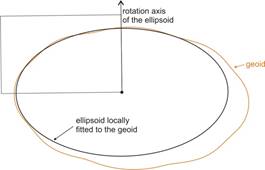
The height above the ellipsoid and the geoid (sea level) are in general different. The difference of the ellipsoidal height and the so called „normal height” (measured on the geoid) is the „undulation of the geoid”. Its values vary between –106 m and 85 m in the case of WGS84 datum.

Replacing the ellipsoid by sphere

Under the map scale cca. 1:1 million (in the geocartography), the coordinate differences on the map caused by the eccentricity of the ellipsoid are smaller than the maximum accuracy of the map (0.1–0.2 mm). So the geocartography uses rather spherical coordinates instead of ellipsoidal in order to simplify the projection calculations. The radius of the sphere can be calculated e.g. by the average of several values of meridian radius of curvature which varies depending on the latitudes of the points on the area of representation. An other usual simple approximation of the mean value of the radius R:

Some projections in the geodesy use an intermediate spherical surface (so called „aposphere”) between the ellipsoid and the map plane. If the mapping is conformal, then the radius R of the osculating sphere, concerning the centre of the area to be represented with ellipsoidal latitude F_s, is defined by the geometric mean of the meridian radius of curvature (M) and the radius of curvature normal to the meridian (N):

Transformations of geographic coordinates between different reference surfaces

The Earth coordinates created in different times and in several circumstances refer to different ellipsoids, datums or substituting spheres. If these mixed coordinates are used together, they have to be integrated in a common reference system. It can be done by transforming the coordinates from a geodetic datum onto another one. In other cases the surface of the ellipsoid is approximated by sphere; on such occasions the coordinates of the ellipsoidal surface are transformed onto spherical coordinates or reversely.

Transformations between geographic coordinates of different datums

The geographic coordinates of Earth’s points originate, directly or indirectly, in geodesic measurements. Exact transformation between different geodetic datums  doesn’t exist in general, due to measuring errors and varied fitting of the ellipsoids, therefore divers approximating transformation methods were developed.

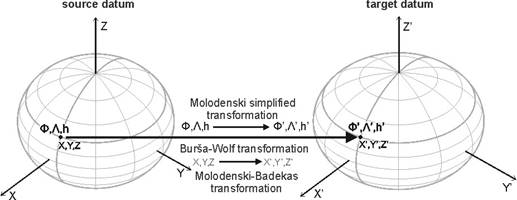
Three-parameter Molodenski simplified transformation between geographic coordinates of different datums

The rotation axes of the source and target datums are supposed parallel, and the transformation comes true by a translation of the origin in a spatial rectangular coordinate system, whose parameters are DX, DY, DZ. The difference Da of the semi-major axes (Da = a_target–a_source) and also the difference Df of the flattenings (Df = f_target–f_source), belonging to the datums in question are additionally used. The simplified formulae of the transformation are given in a way, which doesn’t require transformation between the geographic coordinates (+height above sea level) and the spatial rectangular coordinates to and from, so the calculations can be processed by formulae immediately with the geographic coordinates. Let the geographic coordinates (with the height) of the point to be transformed, be denoted by  F,L,h  on the source datum and  by F’,L’,h’  on the target datum. Then the differences  DF = F’–F,  DL = L’–L,  Dh = h’–h  generated by the transformation, given by the following formulae:

Adding this coordinate differences to the source coordinates, an approximation of the target coordinates will be obtained. For the transformation of points located on a given territory, fitting points with coordinates known in both reference system are required. The DX, DY, DZ parameters characterizing the given territory can be calculated from this fitting points.

Seven-parameter Burša-Wolf transformation between spatial rectangular coordinates of different datums

The Helmert-transformation of spatial points is well-known in the field of geodesy. It is composed of a translation, three rotations and a similarity transformation. The seven parameters are: the components  DX, DY, DZ  of the translation vector, the rotation angles  e_X,  e_Y and e_Z about the axes of the spatial coordinate system, and  the ratio  (1+k)  of the similarity transformation (scaling up or down). Supposing that the rotation angles are small, the formula below assigns the transformed coordinates X’, Y’, Z’ to the spatial point given by coordinates X, Y, Z:

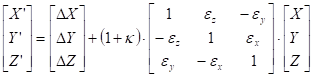
If the source point is given by geographic coordinates (and by its height), then at first their conversion into spatial rectangular coordinates is needed. In the next step they will be transformed by the formulae above. Finally, the obtained spatial rectangular coordinates have to be re-converted into geographic coordinates (+height) using the formulae of Bowring or Borkowski. This is called Burša-Wolf transformation in the field of GIS.

Applying this formula, the transformation of a point on a given territory also demands fitting points with coordinates known in both reference system. The parameters for translation, rotation as well as scaling up or down can be obtained from fitting points with the help of adjustment calculations.

Ten-parameter Molodenski-Badekas transformation between spatial rectangular coordinates of different datums

This transformation takes the same conversions into consideration, as the previous one, but the centre of rotation axes and the similarity transformation is not the origin, but the centroid (that is the point with average coordinates of the triangulation network points on the territory to be represented). So:

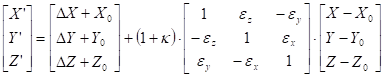
where the coordinates of the centroid are:

,  , 

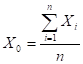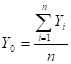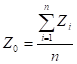
and the points with coordinates (X_i,Y_i,Z_i) (i=1,…,n) are triangulation network points.

Transformation of the ellipsoid onto the sphere

The map projections which use the mentioned intermediate aposphere in the course of mapping from the ellipsoid onto the map plane, need a special built-in transformation, that is to say the mapping of an ellipsoid or its part onto a locally approaching sphere. The basic properties of this transformation are: the ellipsoidal parallels are projected onto spherical ones, otherwise: the spherical latitude depends only on the ellipsoidal latitude, that is j=j(F). Similarly, every ellipsoidal meridian is projected onto a spherical one, moreover the longitude differences on the ellipsoidal parallels have to be proportional to the differences on the sphere, which is expressed in the following formula:  Dl=n×DL, where  n  is constant. The function  j=j(F)  and the constant n  determine the transformation.

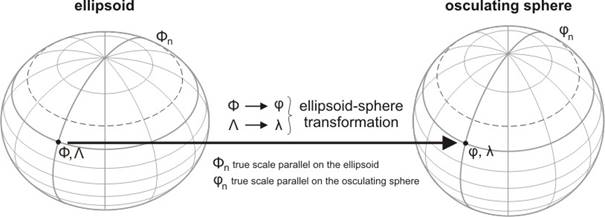
Conformal projection of the ellipsoid onto the sphere

There are mappings from the ellipsoid to the sphere with different distortion properties. The projection can be e.g. equivalent (equal area) if the surface area of every shape of the ellipsoidal surface does not change during the mapping onto the correspondent shape of the spherical surface. An other possible requirement is that the lengths along the meridians do not change during the mapping (in other words the meridians are true scale). Both mappings are used rather in the geocartography.

The geodesy and the GIS demand conformal projections for the mappings from the ellipsoid to the sphere. The property of conformality (or angle invariance) means the preservation of angular relationships in the course of this mapping, and it can be described by equations which result in the following connection between the spherical latitude j and the ellipsoidal latitude F:

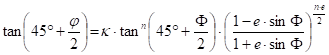
This formula allows the expression of the spherical latitude that is the function j(F):

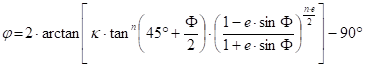
Reversaly, the ellipsoidal latitude can be calculated per iteration:

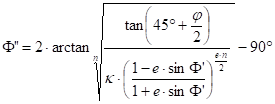   then       until  

where e  is the required accuracy of the calculation;  finally F=F”. A possible initial value: F’=j .

The constants  k  and  n  depend on the aim of the map using the projection with this built-in mapping. If the complete Earth or its large part has to be represented, then it is needed that  n=1. If the ellipsoidal Equator (F=0°) has to be mapped to the spherical Equator (j=0°), then this condition results in  k=1. The still missing radius of the target sphere can be obtained, if a true-scale parallel (where the ellipsoidal lengths and the correspondent spherical lengths equal) is prescribed. Let  F_s  be its latitude on the ellipsoid, and  j_s  on the sphere, then the radius R of the target sphere can be calculated with these quantities:

In other practical cases, when a smaller part of the ellipsoid is mapped to the spherical surface (e.g. by geodesic or topographic maps), a possible ambition can be that the scale distortion on the represented territory should be minimal. This condition leads us to a non-linear system of equations which provides the latitudes of the true scale parallel, the constants n and k, and the radius R. The map projections applied in the geodesy and topography are constructed for the representation of a definite territory, and the constants above are available from preliminary calculations.

Exercise

Given the WGS84 geographic coordinates  and the normal height of the point  mount Ağri Daği  (Turkey)

WGS84 coordinates:      F = 39°42’6.78” L = 44°17’53.94”

normal height = 5137 m

Asked the S42 geographic coordinates of the same point

Necessary concept:   undulation of the geoid = ellipsoidal heigh - normal height (height above sea level)

(its value is about 20.5 - 40 m in Turkey, 40 - 46 m in Hungary, related to the WGS84 datum)

Geoid undulation calculator:

https://www.unavco.org/software/geodetic-utilities/geoid-height-calculator/geoid-height-calculator.html

Solution:

geoid undulation » 21.5 m  (computed by the geoid undulation calculator above)

ellipsoidal height (height above the WGS84 datum) = normal height + geoid undulation » 5137 m +21.5 m = 5158.5 m

Spatial rectangular coordinate differences between the WGS83 and S42 (Krasovskiy) datum:

DX = - 28.0; DY = 130.0; DZ = 95.0;

Differences between the correspondent geographic coordinates and ellipsoidal heights of the WGS84 and S42 datums

s1 = -sin(F)*cos(L)/M(F) = -0.7186883008×10^-7        s2 = -sin(F)*sin(L)/M(F) = -0.7012973154×10^-7

s3 = cos(F)/M(F) = 0.1209431772×10^-6;            s4 = (a*Df+f*Da)*sin(2*F)/M(F) = -0.4178825276×10^-6

arc(DF) = s1*DX+s2*DY+s3*DZ+s4 = 0.3967181444×10^-5

s5 = -sin(L)/N(FF)/cos(FF) = -0.1421257430 10^-6           s6 = cos(L)/N(FF)/cos(FF) = 0.1456502207 10^-6

arc(DL) = s5*DX+s6*DY = 0.00002291404949

s7 = cos(FF)*cos(L) = 0.5506544304       s8 = cos(F)*sin(L) = 0.5373295674        

s9 = sin(F) = 0.6387931076          s10 = (a*df+f*da)*sin(F)^2-da = -109.1035781

Dh = s7*DX+s8*DY+s9*DZ+s10 = 6.0162868 m

DF = 0.0002273027532° DL = 0.001312878327° Dh = 6.0162868 m

S42 coordinates:              F’ = 39°42’7.5983” L’ = 44°17’58.6663”

elipsoidal height » 5164.516287 m                         undulation related to S42 datum » 27.5 m