Coordinate systems on the maps

Map projections and distortions

The maps – both the printed paper maps and the screen maps – in most of the cases have a planar rectangular coordinate system, even if it is not marked on the map. It can satisfy both military and civil purposes in the navigation and geographic location, furthermore it is applied in planning and construction of engineering projects. There are world wide map coordinate systems, in other cases the coordinate system is extended to a country or an empire, or it is used locally (e.g., in an urban or an industrial area). A map sheet can have its own separate coordinate system, too.

Sometimes a planar polar coordinate system can be created on a map, mostly as an intermediate system.

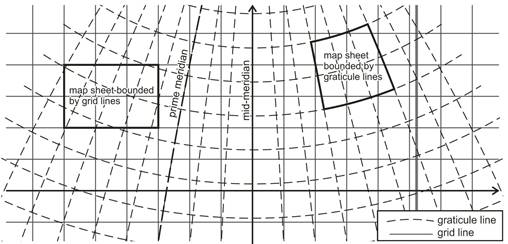
Graticule and grid lines

The graticule lines and the rectangular coordinate lines (in other words the grid lines on the map) generally are not parallel to each other. The map graticule has at least one axis of symmetry coinciding with a meridian, the so called „mid-meridian” or „central meridian” (mostly not identical with the prime meridian), which runs along the midline of the area to be represented. The direction of this axis is the „grid north”, while the tangent of the meridian gives the „true north” (in other words „geodetic north”) at every point of the map. In most instances the topographic map sheets are bounded by graticule lines, while some kinds of cadastral maps are bounded by grid lines.

Transformation of coordinates from the Earth to the map by map projection

The map coordinates are in mathematical connection with the mapped Earth coordinates. This mapping – the map projection – comes true by the projection equations (actually functions) which  assign the map coordinates  x, y  to the coordinates  j, l  in case of spherical reference surface:

.

If the same mapping functions are referred to the metacoordinates j*, l*, the mapping

considered as identical to the previous one but it is appropriate for representing an other territory. (In this case, the map coordinates are calculated mostly in two steps from the Earth coordinates by inserting the metacoordinates:  j, l ® j*, l* ® x, y.) The previous version is called normal (polar) projection, and  the latter is transverse (equatorial) or oblique projection, whether the metapole is situated on the equator (transverse) or anywhere except the pole and the equator (oblique).

It is favourable in the course of map projection calculations, if the inverse of the projection equations is available, in case of sphere:

or

.

In the case of ellipsoidal coordinates  F, L,  the projection equations take the general shape

and the inverse of the projection equations:

Some kinds of projections, so the well-known normal azimuthal, cylindrical and conical projections result in rectangular graticule. Some of them in transverse and oblique versions, and some of non-conic projections also have this property.

Map distortions

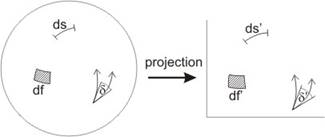
In the course of the planar representation of the Earth surface objects (so arcs, figures, directions), some of their sizes (lengths, areas, angles) change  which makes the use of maps and map coordinates difficult in practice, mainly for the purpose of determining the original extents. These are mathematically formulated in the so called map distortions, viz. the linear scale  l,  the area scale  p and the angular distortion  i, one after the other:

,               ,           

where ds, ds’, df, df’ are infinitesimal quantities, in addition d and d’ are the corresponding angles on the reference surface and on the map plane.

The consequence of the fundamental statement of the differential geometry, the Gauss’s Theorema Egregium, is that the Earth cannot be represented on a map without distortion. Specifically, the linear scale cannot be eliminated, but there are projections without area distortions (the so called equal-area  or equivalent projections), and similarly without angular distortions (the so called conformal projections), while the so called aphylactic projections are neither conformal, nor equivalent. Both the military and the civil topography (inclusive of cadastral cartography) use generally conformal projections, many kinds of thematic maps are created in equal-area projection, and most of the chorographic maps has an aphylactic projection.

According to Tissot’s construction, the area, scale and angular distortions at every point of the map can be calculated with the help of maximum and minimum linear scales (denoted by  a  and  b), whose direction is perpendicular to one another either on the reference surface or on the map. These are determined by the graticule distortions, namely the linear scale  h  along the parallel, the linear scale  k  along the meridian, and the angle Q between the graticule lines, in accordance with the next formulae:

and       

where in the case of projections of sphere with radius  R:

,             ,           

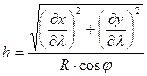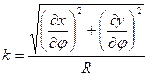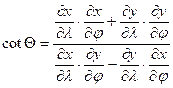     and        .

The scale distortions along the graticule lines in case of ellipsoidal projection:

,           

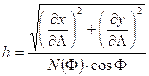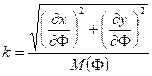
The formula for the area scale  p  is:

If the direction of the maximum scale distortion a and a questionable direction include the angle  d, the linear scale along the latter direction is:

If one of the arms of an arbitrary angle coincides with the direction of the maximum linear scale a, then the angular distortion  i  refering to this angle:

If neither of the arms of the angle d coincides with the direction of the maximum linear scale a, then writing the angle d as difference of the angles  m  and  n  (in formula  d=m-n)  where one of the arms of both  m and n  coincide with the direction of  a, then the angular distortion  i:

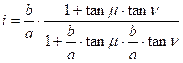
In effect the distortions are determined ultimately by the projection equations.

In consequence of the points described above, the conformality that is the equality  d’=d  for every angle d  on the reference surface, can be given by the equation

and similarly the equivalency by

.

In case of rectangular graticule (or metagraticule), the maximum and minimum linear scales come up along the direction of graticule lines, therefore they can be calculated by simpler formulae. So the equation of the conformality is

 ,

and the equation of the equivalency is

  concerning the graticule (or the metagraticule, in case of transverse or oblique projections).

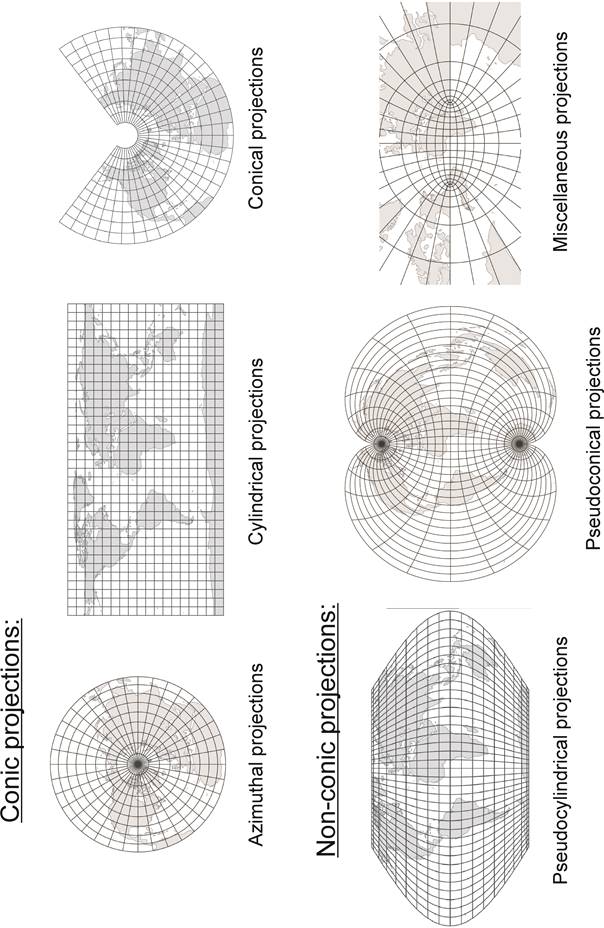
Classification and characterization of the map projections

While the fundamental property of the map projections is their distortion character, the map projections are classified, for illustrative reasons and according to their application, primarily by the character of their graticule.  Based on this, the main groups are: conic projections (namely azimuthal, cylindrical, conical ones) and non-conic projections (pseudocylindrical, pseudoconic including the polyconic, miscellaneous ones). The projections of the second main group are applied mostly for the small scale maps, while the topocartography and the GIS use mainly the conic projections.