ÁTSZÁMÍTÁSOK AZ ALAPFELÜLET KÜLÖNFÉLE KOORDINÁTARENDSZEREI KÖZÖTT

A geodéziai számítások alapfeladatai

A geodéziai koordinátarendszerekben elvégzett számítások gyakran visszavezethetők a földrajzi koordinátarendszerek és a forgásfelületi polárkoordinátarendszerek közötti átszámításokra, az ún. alapfeladatokra.

Első geodéziai alapfeladat fogalma és végrehajtása

Az első geodéziai alapfeladat (másképpen főfeladat, direkt probléma) során egy földrajzi koordinátáival adott pontból kiindulva, egy másik pont irányának és távolságának, vagyis a polárkoordinátáinak ismeretében számítjuk ki annak földrajzi koordinátáit.

Az alapgondolat megértéséhez először legyen adott a síkon az O(x₀,y₀) pont. Ha ismerjük az O és a P pont s távolságát, valamint az OP iránynak az ordináta tengely pozitív felével bezárt, az óramutató járásával megegyezően irányított d irányszögét, akkor a P pont derékszögű koordinátáit a már ismert

képletekből nyerjük.

R sugarú gömb alapfelület esetén az O(j₀, l₀) pont mellett adott az O és a P pont s távolsága, valamint az a₀ azimut. A P pont j,l földrajzi koordinátáit gömbháromszögtani úton határozhatjuk meg. Induljunk ki az NOP polárgömbháromszögből. Írjuk fel az oldal-koszinusztételt az O ponttal szemközti oldalra:

Ebből a képletből kifejezhető j:

A Dl=l-l₀ hosszúságkülönbség a szinusztételből adódik:

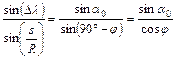
Ha tudjuk, hogy Dl hegyes- ill. tompaszög, akkor ebből a képletből kifejezhető:

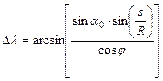
Ellenkező esetben – ami elsősorban távoli O és P pont esetén fordulhat elő – a Dl korrekt kiszámításához a szinusza mellett a koszinuszára is szükség van. Ez a Dl szöggel szemközti oldalra felírt oldal-koszinusztételből jön:

és

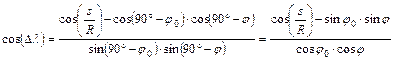
A Dl szöget ezek után az alábbi képlet szolgáltatja:

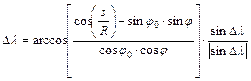
Végül a l hosszúságot a

képlet adja meg.

A fenti képlete csak akkor érvényes, ha a nevező nem zérus. Ezekben az esetekben viszont a képletre nincs is szükség, ugyanis

• cosj₀=0 esetén az O pont vagy az N pólusban van, és ekkor Dl= -a₀; vagy pedig az O pont az N ponttal átellenes S pólusra esik, és ekkor Dl= -a₀;
• cosj=0 esetén a P pont esik az N vagy az S pólusba, márpedig a pólusban a hosszúságnak akármilyen értéket tulajdoníthatunk;
• sina=0 esetén a P pont az O és N által meghatározott bimeridiánra esik, és ekkor Dl értéke vagy zérussal vagy 180°-kal egyenlő, attól függően, hogy a bimeridián melyik ívén helyezkedik el.

Forgási ellipszoid alapfelületen az O(F₀,L₀) origó-választás esetén – a P pontra vonatkozó s ellipszoidi ívhossz és a₀ azimut ismeretében – a P pont (F,L) koordinátáinak kiszámítására többféle módszer ismeretes. Ezek közül Legendre-nak az alábbiakban bemutatandó módszere hatványsorral számítja ki a keresett földrajzi koordinátákat.

Az origóból a₀ azimuttal kiinduló geodetikus vonal mentén mind a F szélesség, mind a L hosszúság, mind pedig a vonal a azimutja változik az s ívhossz függvényében:

Sorbafejtve ezeket s=0 körül:

Vegyük a geodetikus vonal egy kicsiny, Ds ívhosszú darabját, melynek végpontjait A-val és B-vel, a B ponton áthaladó parallelkörnek az A-n áthaladó meridiánnal való metszéspontját T-vel, az A-nál keletkezett szöget a-val jelöljük (???ábra). Az AT meridiánív hossza DF, tehát az ABT alakzatot közelítőleg derékszögű síkháromszögnek tekintve és határátmenetet végezve:

Ugyancsak az ABT alakzatból – tekintetbe véve, hogy az AT ív egy N(F)×cosF sugarú parallelkör DL középponti szöghöz tartozó része – következik határátmenettel, hogy

Végül Clairaut korábban említett tételéből, mely szerint a forgásfelületek geodetikus vonalai mentén a parallelkör sugarának az azimut szinuszával képzett szorzata állandó, következik a forgási ellipszoidra, hogy

Ezt deriválva s szerint kapjuk, hogy

(A baloldalon álló kifejezés mind F-n, mind a-n keresztül függ s-től, ezért a láncszabályt alkalmaztuk.) Behelyettesítve ide N(F), M(F) és dF/ds képletét és figyelembe véve, hogy

,

majd elvégezve az egyszerűsítéseket és összevonásokat, kapjuk, hogy

Innen:

Ezek a deriváltak F=F₀ és a=a₀ helyettesítésnél adják a fenti hatványsorok elsőfokú tagjainak együtthatóját.

Tovább folytatva az s szerinti deriválást, kapjuk, hogy

Ezekbe helyettesítve a P₀ pontbeli értékeket, kapjuk a hatványsorok másodfokú tagjainak együtthatóját.

Hasonlóan folytatható a magasabb fokú tagok együtthatóinak kiszámítása. A harmadrendű deriváltak pl.:

A geodéziai feladatok által megkövetelt pontossághoz esetenként – a viszonylag lassú konvergencia miatt – F és L esetében az ötödfokú tagot, a esetében pedig a negyedfokú tagot is figyelembe kell venni.

Fokozatos közelítéssel, de kevesebb számítással adja az eredményt Gauss középszélesség-módszere. Ennek alapelve annyiban különbözik Legendre módszerétől, hogy a hatványsorokat a konvergencia javítása céljából a két pontot összekötő s ívhosszú geodetikus vonal (egyelőre ismeretlen F_f, L_f koordinátájú és a_f azimutú) P_f felezőpontjából kiindulva írja fel. A P_f közelítéséhez felhasználja az ismert P₀ és az egyelőre ismeretlen, de ismertnek feltételezett P végpont koordinátáinak átlagolásából adódó P_m pontot (???ábra), melynek koordinátái tehát a

középértékek. A F(t), L(t) és a(t) függvények P_f felezőpont körüli sorfejtései:

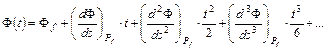
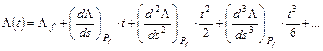
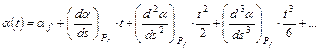
Helyettesítsünk az első hatványsorba t helyére (s/2)-t és (– s/2)-t; ekkor a végpontok szélességét kapjuk meg:

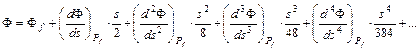
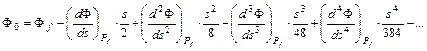
Ezeket egymásból kivonva kapjuk a végpontok DF szélességkülönbségét:

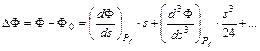
ahol a P_f felezőpontra vonatkozó deriváltakat egyelőre nem ismerjük. Írjuk fel a P_f pont F_f szélességének és a hozzá közel eső, a koordináták középértékeivel megadott P_m pont F_m szélességének F_m–F_f eltérését:

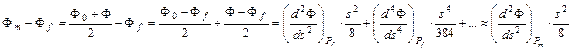
A másodfokú tag (ismert) P_m pontbeli értékének segítségével a F_f szélesség innen már közelíthető:

Hasonlóan kapható L fenti sorfejtéséből (s/2) és (– s/2) behelyettesítése után, hogy

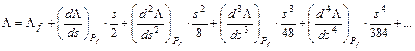
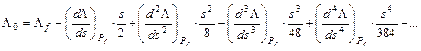
Innen kapjuk kivonással a végpontok DL hosszúságkülönbségét:

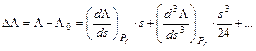
A L_f meghatározása céljából írjuk fel a L_m–L_f eltérést:

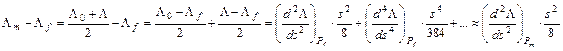
Innen közelítőleg kapjuk L_f-t:

Végül ha a sorfejtésébe helyettesítjük be (s/2)-t és (– s/2)-t:

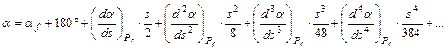
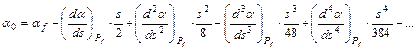
Kivonással adódik a Da azimut-különbség:

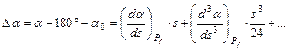
A P_f pontbeli a_f azimut kiszámításához szükség van az a_f–a_m eltérésre:

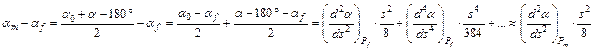
Ebből már közelítőleg számítható a_f :

A P_f pont koordinátáinak ismeretében meghatározzuk a DF, DL és Da különbségeket, és ezeket hozzáadva az O pontra vonatkozó értékekhez, megkapjuk a keresett P pont F, L és a jellemzőit:

A fentiekben leírt műveletsor elkezdéséhez szükség van a P pont valamilyen közelítő értékére, amelyre megfelelnek pl. az R sugarú gömbre érvényes koordináták, valamilyen közelítő R választásával. A műveletek eredményeként kapott F, L és a a P pont tényleges koordinátáinak a kezdőértékeknél jobb közelítései. Ezeket visszahelyettesítve a műveletsor elejére, újabb közelítést hajthatunk végre még jobb F, L és a megkapása érdekében. Ezt addig ismételjük, amíg a műveletsor kiindulási és végeredményként kapott F, L és a értékei közti különbségek a kívánt pontossági küszöb alá csökkennek.

Második geodéziai alapfeladat fogalma és végrehajtása

A második geodéziai alapfeladat (másként főfeladat, inverz vagy fordított probléma) arra irányul, hogy egy földrajzi koordinátáival adott pontból kiindulva, egy másik pont földrajzi koordinátáinak ismeretében e pont irányát és távolságát, vagyis a polárkoordinátáit határozzuk meg.

Az alapgondolat megértéséhez most legyen adott a síkon az O(x₀,y₀) és a P(x,y) pont; ebből kell kiszámítani az s-sel jelölt OP távolságot és az OP vektornak az ordináta tengely pozitív felével bezárt, az óramutató járásával megegyezően irányított d irányszögét a már ismert képletek alkalmazásával:

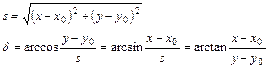
Tekintsük most az R sugarú gömbfelületen az ismert koordinátájú O(j₀, l₀) és P(j,l) pontokat; meghatározandó a pontok s gömbi távolsága és az O pontbeli a azimut. Ez a feladat is gömbháromszögtani összefüggésekkel oldható meg. Az NOP polárgömbháromszögben írjuk fel a Dl=l-l₀ szöggel szemközti, s hosszúságú oldalra az oldal-koszinusztételt (tekintetbe véve, hogy az s oldalhosszt s/R középponti szögben kell megadni):

Innen kifejezhetjük az s/R szöget:

Ez a radiánban megadott szög adja R-rel való szorzás eredményeként az s hosszat az R hossz-mértékegységében.

Az a azimut kiszámításához szükségünk van az NOP polárgömbháromszög O pontnál lévő w belső szögére. Felírva a szinusztételt:

Ha tudjuk, hogy w hegyes- vagy tompaszög, akkor innen w kifejezhető:

Ellenkező esetben w meghatározásához szükségünk lesz a koszinuszára is, amelyet az O ponttal szemközti oldalra felírt oldal-koszinusztételből kapjuk meg:

és

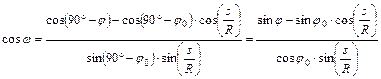
Most az w szög abszolút értékét a cosw-ból, előjelét pedig a sinw-ból kapjuk, hozzátéve, hogy a sinw előjelét a sinDl tényező határozza meg; tehát:

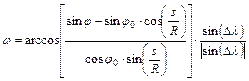
Ha a P pont O-tól K-re fekszik, akkor a=w, fordított esetben a=360°-w.

Forgási ellipszoid alapfelület esetén a P₁(F₁,L₁) és P₂(F₂,L₂) végpontok közötti s ellipszoidi ívhossz, valamint a P₁ pontbeli a₁ és a P₂ pontbeli a₂ azimut kiszámítása Gauss középszélesség-módszerével történik.

Átszámítás a földrajzi és a segédföldrajzi koordináták között

A fokhálózat átvitelét egy segédföldrajzi fokhálózatba elforgatási transzformációnak nevezzük, mert a gömbközéppont körüli elforgatásokkal valósítható meg. A transzformáció végrehajtásához szükség van a P pont (j,l) földrajzi koordinátái és (j*,l*) segédföldrajzi koordinátái közötti átszámítás képleteire.

Átszámítás a segédpólus és a segéd-kezdőmeridián ismeretében

Alapértelmezésben tekintsük adottnak az N* segédpólust az eredeti földrajzi koordinátarendszerbeli j₀,l₀ koordinátákkal, és haladjon át a segéd-kezdőmeridián pl. az N északi póluson. (Ellenkező irányítás esetén a segédhosszúságok 180°-kal megváltoznak, míg a segédszélességek változatlanok maradnak.)

aa) Legyen először ismert (j,l), és keressük (j*,l*)-ot. A P(j,l) pont az N és az N* ponttal egy gömbháromszöget alkot (???ábra), amelynek oldalai sorra: 90°-j₀ , 90°-j* és 90°-j, az N*-nál lévő szöge a l* segédhosszúság, N-nél lévő szöge pedig a

hosszúságkülönbség. (Megjegyzendő, hogy Dl és l* az ellentétes irányítás miatt ellenkező előjelűek.)

Írjuk fel az oldal-koszinusztételt az N pólussal szemközti oldalra:

.

Innen kapjuk, hogy

Ha a P pont valamelyik segédpólussal egybeesik, vagyis

,

akkor a l* segédhosszúság ott nincs értelmezve, tehát l*-nak bármilyen érték tulajdonítható. Ha pedig a P pont az N* és az N pontok által meghatározott bimeridiánra esik, vagyis

, vagy ,

akkor

vagy

attól függően, hogy P a bimeridián melyik részén helyezkedik el.

Ha ezen esetek közül egyik sem áll fenn, és a segédpólus mindkét eredeti pólustól különbözik, vagyis

,

akkor felírható az oldal-koszinusz tétel az N* ponttal szemközti oldalra, amiből kifejezhető a

l* segédhosszúság:

.

és ezzel megkaptuk a P pont segédföldrajzi koordinátáit.

Speciálisan ha az N* segédpólus az egyenlítőn helyezkedik el (vagyis j₀=0°, ???ábra), akkor ,

továbbá a szinusz-tételből

,

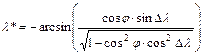és az oldal-koszinusztételből

.

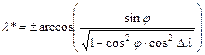ab) A fenti fokhálózat-transzformáció fordítottja a segédföldrajzi (j*,l*) koordinátákból a (j,l) földrajzi koordináták kiszámítása. Az iménti jelölések mellett tekintsük ismét az N pólus, az N*(j₀,l₀) segédpólus és a P(j*,l*) pont által meghatározott gömbháromszöget.

Az N* segédpólussal szemközti oldalra felírt oldal-koszinusztétel:

Innen kifejezhető a j szélesség:

Elmondható itt is, hogy ha a P pont valamelyik pólussal egybeesik, vagyis

,

akkor a Dl hosszúságkülönbség ott nincs értelmezve, tehát Dl-nak bármilyen értéket tulajdoníthatunk. Ha viszont a P pont az N* és az N pontok által meghatározott bimeridiánra esik, vagyis

, vagy ,

akkor

vagy

attól függően, hogy P a bimeridián melyik részén helyezkedik el.

Ha ezen esetek közül egyik sem áll fenn, és a segédpólus mindkét eredeti pólustól különbözik, vagyis

,

akkor itt is felírható az oldal-koszinusz tétel az N ponttal szemközti oldalra, amiből kifejezhető a Dl hosszúságkülönbség:

,

és ebből kapjuk a l hosszúságot:

.

Átszámítás a segédegyenlítő és a segéd-kezdőmeridián metszéspontjából kiindulva

Ha a földrajzi és segédföldrajzi koordináták közötti átszámítások a segédegyenlítő környékének pontjait érintik, akkor az átszámítások másik típusa kerül előtérbe. Itt nem az N* segédpólus koordinátái, hanem a segédegyenlítő és a segéd-kezdőmeridián K metszéspontjának (j_K,l_K) koordinátái vannak megadva, és pl. a segédszélesség növekedésének iránya. (Megjegyezzük, hogy ilyen számításokat általában csak a K középponttal meghatározott félgömbön belül szoktunk végezni, ezért a továbbiakban megadott képletek csak a K-tól 90°-nál nem nagyobb gömbi távolságú pontokra érvényesek.) A segéd-kezdőmeridián most kivételesen nem az N északi póluson, hanem a K ponton halad át, tehát az egyenlítőre esik; így ennek K-ból kiinduló negyedkörnyi íve kijelöli az N* segédpólust (???ábra). A P, N és N* csúcspontok által meghatározott gömbháromszög oldalai sorra j_K, 90°-j* és 90°-j, az N csúcsnál lévő szöge 180°-Dl, a l* segédhosszúság pedig az egyenlítőnek az N*P segédmeridiánnal bezárt (előjeles) szöge.

ba) A (j*,l*) segédföldrajzi koordináták kiszámításához írjuk fel az N csúccsal szemközti oldalra az oldal-koszinusz-tételt:

Innen kapjuk, hogy

.

Másrészt írjuk fel az N és N* csúcsokra vonatkozó szinusztételt:

.

Innen a műveletek végrehajtása után kifejezhető l*:

.

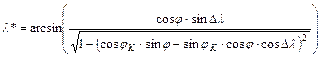Gyakrabban használt az a képlet, amelyet tgl*-ból kaphatunk. Írjuk fel ehhez az N* csúccsal szemközti oldalra az oldal-koszinusztételt:

Innen fejezzük ki cosl*-ot, és sinj*-ba helyettesítsük be a fent nyert kifejezést. Összevonások és egyszerűsítés után:

Ezt felhasználva:

.

Végigosztva cosj -vel, és elvégezve az egyszerűsítést:

,

és így ebben a változatban is megkaptuk a P pont segédföldrajzi koordinátáit.

Ha itt az N* segédpólus az egyenlítőre esik, akkor a K vetületi kezdőpontot nem a pólusban, hanem az egyenlítő és a (segédegyenlítővel egybeeső) középmeridián metszéspontjában célszerű felvenni (???ábra). Ekkor az oldal-koszinusztételből:

és a műveletek elvégzése után:

.

A másik oldal-koszinusztételből:

,

és innen:

.

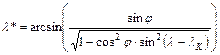bb) Hátra van még itt is a segédföldrajzi (j*,l*) koordinátákból a (j,l) földrajzi koordináták kiszámításának módja. Induljunk ki ismét az N pólus, a K(j_K,l_K) vetületi kezdőpont által kijelölt N*(j₀,l₀) segédpólus és a P(j*,l*) pont által meghatározott gömbháromszögből. Írjuk fel az N* csúccsal szemközti oldalra az oldal-koszinusztételt:

Ebből következik, hogy:

A szinusztételből ismét

.

A műveletek elvégzése után:

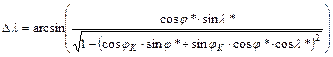
A tgDl –ból származtatandó képlethez írjuk fel az oldal-koszinusztételt az N csúccsal szemközti oldalra:

,

Innen fejezzük ki cosDl -t, és sinj -be helyettesítsük be az imént kapott kifejezést. Összevonva és egyszerűsítve:

Ezt felhasználva:

.

Végigosztva cosj* -gal, majd elvégezve az egyszerűsítést:

,

végül ebből jön a l hosszúság:

.