ELLIPSZOID-ALAPFELÜLETÛ VALÓDI VETÜLETEK A GEOKARTOGRÁFIÁBAN ÉS A TOPOKARTOGRÁFIÁBAN

Az ellipszoidot elsõsorban a nagyobb méretarányú térképek alapfelületeként használják. Általánosságban elmondható, hogy egy kb. 1 milliós méretarányú térképen már jelentkezik a gömb és ellipszoid alapfelület közötti különbség. Készültek ennél nagyobb (pl. 750 ezres) méretarányban térképek gömb alapfelülettel, másrészt van ennél jóval kisebb (pl. 2.5 milliós) méretarányú térképmû, amelyhez ellipszoid alapfelületet használtak.

Ellipszoid-alapfelületû vetületeken olyan vetületeket értünk, amelyeknek vetületi egyenletei közvetlenül rendelik hozzá az  x,y  síkkoordinátákat egyrészt a  F  ellipszoidi szélességhez (vagy a  B  ellipszoidi pólustávolsághoz), másrészt a  L  hosszúsághoz:

vagy

Az ellipszoid alapfelületû vetületeket a gömb alapfelületûekhez hasonló csoportosításban tárgyaljuk.

Valódi vetületek ellipszoid alapfelülettel

Az ellipszoid-alapfelületû vetületek idetartozó nagy csoportja rendelkezik a valódi vetületek fokhálózatára vonatkozó tulajdonságokkal:

- a parallelkörök képei ekvidisztáns koncentrikus körök, a meridiánok képei egy pontba összefutó egyenesek (valódi síkvetületek);

- a parallelkörök képei ekvidisztáns párhuzamos egyenesek, a meridiánok képei nem feltétlenül ekvidisztáns párhuzamos egyenesek (valódi hengervetületek);

- a parallelkörök képei ekvidisztáns koncentrikus körívek, a meridiánok képei egy pont felé összetartó egyenesek (valódi kúpvetületek);

Valódi síkvetületek ellipszoid alapfelülettel

Kerüljön a síkkoordinátarendszer origója a korábbiaknak megfelelõen a pólusba, és essen a kezdõmeridián az  y  tengely negatív felére. Ekkor r=r(B) -val jelölve a  B pólustávolságú parallelkör képfelületi sugarát (a sugárfüggvényt), a vetületi egyenletek:

Jelölje most  a  és  b  az ellipszoid nagy és kis féltengelyét, e az ellipszoid elsõ excentricitását. A  r(B)  sugárfüggvény meghatározásához induljunk ki az ellipszoidon érvényes fokhálózat menti hossztorzulásokból. A DL hosszúságkülönbséghez tartozó parallelkör menti  Dp

ívhossz a B pólustávolságú parallelkörön:

Az ennek megfelelõ képfelületi  dp’  ívhossz a képfelületen:

A parallelkör menti  h  hossztorzulás tehát:

DB szélességkülönbséghez tartozó meridián menti  Dm  ívhossz:

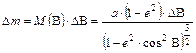
(Itt  M(B) a meridiángörbületi sugár.) Az ennek megfelelõ képfelületi  Dm’  ívhossz:

A meridián menti  k  hossztorzulás tehát:

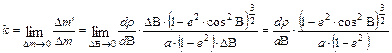
Az ellipszoid alapfelületû vetületek körében ezen  h  és  k  hossztorzulások alapján alkotható meg a meridiánban hossztartó ill. ekvidisztáns, a szögtartó és a területtartó síkvetület.

Meridiánban hossztartó ill. ekvidisztáns síkvetület ellipszoid alapfelülettel

Az ekvidisztáns síkvetületben a térképi meridián menti hosszak arányosak a megfelelõ alapfelületi meridiánhosszal. A sugárfüggvény tehát:

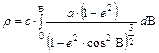
ahol  c  a képfelületi és az alapfelületi hossz aránya;  c=1  esetén a vetület meridiánban hossztartó. (A térképi meridiánok mentén – eltérõen a gömb alapfelületû vetülettõl – a parallelkörök metszésközei nem lesznek egyenlõk, mert az ellipszoid alapfelületen az egyenlítõtõl a pólusig a parallelkörök távolsága növekszik.) A sugárfüggvény képletében szereplõ integrál numerikusan számítandó. Ismeretes sorfejtésbõl adódó sugárfüggvény is. A vetület általános torzulású. c=1  esetén a pólusban nincsen torzulás,  c<1  esetén van egy torzulásmentes parallelkör.

Az 1 : 2.5 milliós világtérképmûben a pólusok környékét a 60°-os illetve a -60°-os szélességig terjedõen ekvidisztáns síkvetületben ábrázolják,  c=0.99 választással. A  75.9432° szélesség (B=14.0568°) hossztartó.

Szögtartó síkvetület ellipszoid alapfelülettel

A topokartográfiában – például a Gauss-Krüger és az UTM vetületi rendszereknél – a pólus környékének ábrázolására is használják a szögtartó síkvetület normális elhelyezésû változatát, de ellipszoid alapfelülettel. Ennek a B  ellipszoidi pólustávolságtól függõ sugárfüggvénye az ellipszoid alapfelületre érvényes szögtartási alapegyenletbõl (a parallelkör menti  h  hossztorzulás és a meridián menti k hossztorzulás egyenlõségébõl) vezethetõ le:

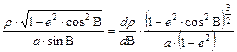
A szétválasztható változójú differenciálegyenletet integráljuk:

Ennek megoldásából kapjuk a r sugárfüggvényt:

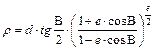
ahol  d  az a konstans, amely kijelöli a hossztartó (és így torzulásmentes) parallelkört.

Ha pl. a pólus torzulásmentes, akkor a

egyenletbõl kapjuk, hogy

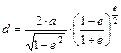
A NATO topokartográfiai világtérképmûjénél alkalmazott UTM vetület a Földet csak a D-i szélesség 80°-tól az É-i szélesség 84°-ig ábrázolja; a pólusok környéke viszont a fenti szögtartó síkvetületben készül, a

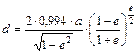
választással. Ez az UPS (Universe Polar Stereographic) elnevezésû vetület (Hayford 1924 alapfelület esetén) a  ±81°6’52.2588” szélességen torzulásmentes, a pólusokban 0.994-szeres hossztorzulás lép fel  (d=12637636.654785).

Ugyancsak a poláris sztereografikus vetületet használják 1962 óta az 1:1 000 000 geokartográfiai világtérképmû pólus ábrázolásához (az É.sz. 84°-tól az északi, illetve a D.sz. 80°-tól a déli pólusig terjedõen). A Hayford 1924 ellipszoid alapfelület választással (d=12621895.458099) a  ±80°14’19” szélességi kör torzulásmentes, a pólusban fellépõ hossztorzulás: 0.99276189.

Területtartó síkvetület ellipszoid alapfelülettel

A pólusok környékének nagyméretarányú, területtartó ábrázolásához ajánlható az ellipszoid alapfelületû területtartó síkvetület. Kiindulva a területtartás alapegyenletébõl:

esetünkben

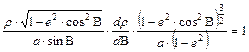
Ez egy szétválasztható változójú differenciálegyenlet, melyet integrálva:

A megoldás:

Ebbõl kapjuk a sugárfüggvényt:

ahol a  r(b=0)=0  (vagyis a póluspontosság) követelménye miatt

Tehát

A pólusban az  l  hossztorzulás egységnyi, emiatt itt nincs torzulás.

Valódi hengervetületek ellipszoid alapfelülettel

A síkkoordinátarendszer origóját az Egyenlítõ és a kezdõ- (közép-) meridián metszéspontjában vesszük fel. Írjuk fel a  fokhálózat  menti hossztorzulásokat.

A DL hosszúságkülönbséghez tartozó parallelkör menti  Dp  ívhossz a  F  szélességû parallelkörön:

Az ennek megfelelõ képfelületi  Dp’  ívhossz a parallelkörök elvárt ekvidisztanciája alapján:

ahol  c  konstans. A parallelkör menti  h  hossztorzulás tehát:

Legyen most a  F_n  szélességi kör hossztartó, ekkor

ahonnan

ami éppen a hossztartó szélességi kör sugara.

Ebben az esetben tehát:

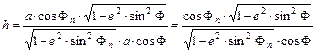
DF  szélességkülönbséghez tartozó meridián menti  Dm  ívhossz:

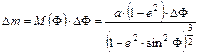
(M(F)  itt is a meridiángörbületi sugár.) Az ennek megfelelõ képfelületi  Dm’  ívhossz egy y irányú elmozdulás, :

A meridián menti  k  hossztorzulás tehát:

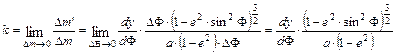
Az ellipszoid-alapfelületû hengervetületek  x  vetületi egyenletének felírásához induljunk ki abból, hogy gyakorlatilag minden hengervetületnek van hossztartó szélességi köre (±F_n), amelynek sugara a fentiekben megadott  c.  Innen:

A  h  és a  k  hossztorzulásokból vezethetõ le a meridiánban hossztartó, a szögtartó és a területtartó ellipszoid-alapfelületû hengervetület  y  vetületi egyenlete.

Meridiánban hossztartó hengervetület ellipszoid alapfelülettel

A meridiánban hossztartó hengervetületben a térképi meridián menti hosszak megegyeznek az alapfelületi ívhosszakkal. Az  y  vetületi egyenlet tehát:

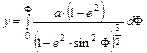
Ez a vetület általános torzulású, a hossztartó parallelkör(ök) torzulásmentes(ek).

Szögtartó hengervetület ellipszoid alapfelülettel

A szögtartás alapegyenletébõl

következik, ami hengervetületek esetén

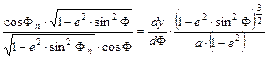
alakú. Innen  dy/dF  kifejezhetõ:

Az integrálást elvégezve kapjuk, hogy

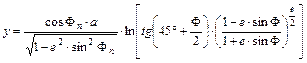
A hossztartó  ±F_n  szélességi kör torzulásmentes.

Területtartó hengervetület ellipszoid alapfelülettel

A területtartás alapegyenletébõl

következik, ami hengervetületek esetén

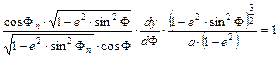
alakú. Fejezzük ki  dy/dF -t:

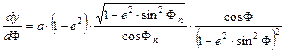
Ezt integrálva kapjuk, hogy

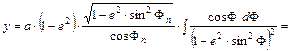
A hossztartó  ±F_n  szélességi kör torzulásmentes.

Valódi kúpvetületek ellipszoid alapfelülettel

Vegyük fel a síkkoordinátarendszer origóját abba a pontba, amely felé a meridiánképek összetartanak, és kerüljön a kezdõ- (vagy közép-)  meridián az  y  tengely negatív felére. Ekkor a szokásos  r=r(B) -val jelölve a parallelkör képfelületi sugarát (a sugárfüggvényt), a vetületi egyenletek:

ahol  n  a térképi meridiánok által bezárt L’ szög és a megfelelõ alapfelületi meridiánok által bezárt L szög aránya (a sugárhajlás).

Írjuk fel az ellipszoidon érvényes fokhálózat menti hossztorzulásokat. A DL hosszúságkülönbséghez tartozó parallelkör menti  dp  ívhossz a B pólustávolságú parallelkörön:

Az ennek megfelelõ képfelületi  dp’  ívhossz a képfelületen:

A parallelkör menti  h  hossztorzulás tehát:

DB szélességkülönbséghez tartozó meridián menti  dm  ívhossz:

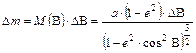
(Itt  M(B) a meridiángörbületi sugár.) Az ennek megfelelõ képfelületi  dm’  ívhossz:

A meridián menti  k  hossztorzulás tehát:

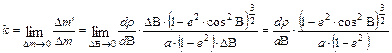
A  h  és  k  hossztorzulásokból vezetjük le  a meridiánban hossztartó ill. ekvidisztáns, a szögtartó és a területtartó kúpvetületet.

Meridiánban hossztartó ill. ekvidisztáns kúpvetület ellipszoid alapfelülettel

A meridiánban hossztartó kúpvetületben a térképi meridián menti hosszak megegyeznek a megfelelõ alapfelületi meridiánhosszal. Ebbõl adódóan a sugárfüggvény:

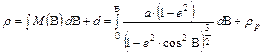
ahol  r_p  a pólusvonal sugara. (Hasonlóan a síkvetületekhez, a térképi meridiánok mentén a parallelkörök metszésközei itt sem lesznek egyenlõk, mert az ellipszoid alapfelületen az egyenlítõtõl a pólusig a parallelkörök távolsága növekszik.) A sugárfüggvény képletében szereplõ integrál itt és a továbbiakban numerikusan számítható. A vetület általános torzulású.

Az  n  sugárhajlás és a  r  sugárfüggvényben szereplõ  d  additív konstans (így a pólusvonal  r_p  sugara) a hossztartó parallelkörök számából és helyzetébõl adódik a következõk szerint:

Legyen  B₁  és  B₂  a két hossztartó parallelkör, és jelölje  r₁  és  r₂  ezek térképi sugarát. Írjuk fel ezekre a hossztartás egyenletét:

és

Egyszerûsítés után vonjuk ki a második egyenletet az elsõbõl:

Felhasználva az ellipszoidi paralelkör sugarára az

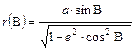
jelölést, kifejezhetjük  n-et:

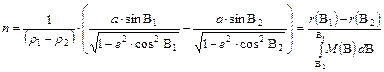
Részletesen:

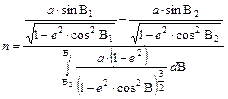
Itt felhasználtuk, hogy a hossztartó parallelkörök  r₁  és  r₂  térképi távolsága – a meridiánban való hossztartás miatt – megegyezik az alapfelületi meridiánív hosszával.

A pólusvonal  r_p  sugara szintén a hossztartó parallelkörökre vonatkozó egyenletekbõl következik:

A meridián menti hossztartásból:

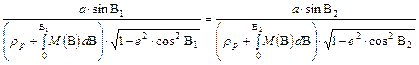
Rövidebben:

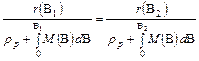
Végezzük el az átszorzást és fejezzük ki  r_p –t:

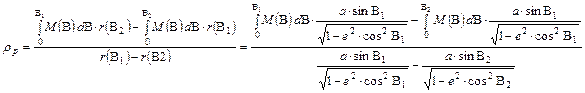
A nevezõt beszorozva és el is osztva a  B₂  és  B₁  közötti meridiánív hosszával, becsempészhetõ az  n.  Elvégezve az átalakításokat, kapjuk a  r_p  egyszerûbb alakját:

Részletesebben:

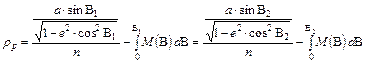
Ezt a vetületet használják a késõbb tárgyalandó 1 : 2.5 milliós világtérképmûben a D-i és É-i szélesség 64°-a közötti terület ábrázolására.

A meridiánban hossztartó kúpvetület egy parallelkörben hossztartó változatánál a  r  sugárfüggvény  d  additív konstansát – r_p  helyett – szerencsésebb a  B_n  pólustávolságú hossztartó parallelkör r_n térképi sugarával kifejezni:

Jelölje w  a képzeletben körgyûrû-cikké kiterített kúp térképi nyílásszögét. A  B_n  parallelkör hossztartásának jelentése:

Innen az  n  sugárhajlás:

Most már felírhatjuk a  h  parallelkör menti hossztorzulást:

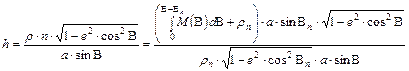
A kúpvetületnek akkor van egyetlen hossztartó parallelköre B=B_n -nél, ha a  h  parallelkör menti hossztorzulás éppen  B=B_n –nél veszi fel a minimumát, vagyis:

Elvégezve a deriválást és a behelyettesítést, az alábbi egyenlethez jutunk:

Az egyenletbõl  r_n  kifejezhetõ:

Ezt visszahelyettesítve az  n  képletébe:

,

ami megegyezik a gömb alapfelületû, egy parallelkörben hossztartó kúpvetület sugárhajlásának képletével.

Szögtartó kúpvetület ellipszoid alapfelülettel

A sugárfüggvényhez a szögtartás alapegyenletébõl (a parallelkör menti  h  hossztorzulás és a meridián menti k hossztorzulás egyenlõségébõl) juthatunk el:

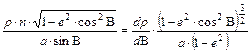
Integráljuk a szétválasztható változójú differenciálegyenletet:

Az egyenlet megoldásából kapjuk a r sugárfüggvényt:

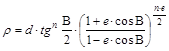
ahol a  d  konstans és az  n  sugárhajlás együttesen jelöli ki a hossztartó (és így torzulásmentes) parallelkört illetve parallelköröket.

Ha  B_n  jelöli az egyetlen hossztartó parallelkört, akkor a hossztartást jelentõ

egyenletbõl és a parallekör menti  h  hossztorzulás minimumát a  B_n-ben kijelölõ

egyenletbõl kapjuk  n  és  d  értékét. Írjuk fel ehhez  h  deriváltját:

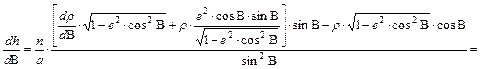
Látható, hogy ennek a kifejezésnek az utolsó tényezõje a  B=B_n  helyen akkor zérus, ha

A hossztartás egyenletébe behelyettesítve a  r  sugárfüggvény képletét, majd az egyenletbõl kifejezve  d -t:

 ,

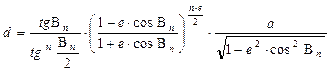ahol  n  már ismert a fenti egyenlõségbõl.

A  B_n  hossztartó parallelkör a szögtartás miatt torzulásmentes.

Ha két hossztartó parallelkörünk van (B₁ és B₂), akkor fejtsük ki a  h(B₁)=1  és  h(B₂)=1  egyenlõségeket:

.

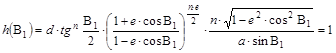
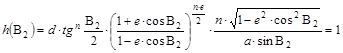E két egyenletet egymással elosztva és egyszerûsítés után a kapott egyenletet logaritmálva, jutunk az

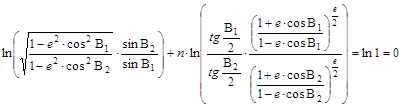
egyenlethez. Ebbõl  n  kifejezhetõ:

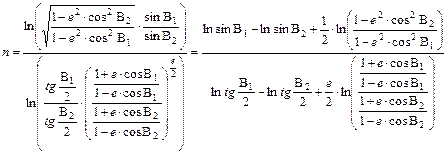
majd  n  segítségével kapjuk  d -t.

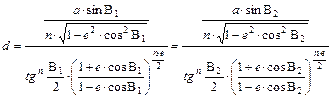
Ezt az  n-et és d -t és  helyettesítve a  r  sugárfüggvénybe, a szögtartó kúpvetületünk a  B₁  és  B₂  szélességû parallekörök mentén torzulásmentes lesz. Ha adott  n  és  d, akkor a  h(B₁)=1  és  h(B₂)=1  egyenlõségek mint nem-lineáris egyenletek megoldásával kapjuk  a hossztartó (és egyben torzulásmentes)  B₁  és  B₂  szélességi köröket.

A Lambert német matematikus-térképésztõl eredõ szögtartó kúpvetülethez az ellipszoidi képleteket a XIX.sz. folyamán fejlesztették ki. A topokartográfia – Lambert-Gauss féle vetület néven – a XX.sz. 10-es éveitõl elterjedten használja országok geodéziai-topográfiai ábrázolásához, majd (pl. léginavigációs célra készült) világtérképmûvekhez. Franciaország pl. az I. világháború óta ebben a vetületben készíti katonai topográfiai térképeit. A D-i Mediterráneum országai Egyiptomtól Marokkóig a topográfiai térképekhez szintén ezt a vetületet alkalmazzák.  Az 1:1000000 méretarányú világtérképmû (IMW) eredeti módosított polikónikus vetületét is ez a vetület váltotta fel 1962 óta.

Területtartó kúpvetületek ellipszoid alapfelülettel

A  r  sugárfüggvényt a területtartás

alapegyenletébõl kiindulva kapjuk meg. Ez kúpvetületek esetén a

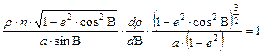
szétválasztható változójú differenciálegyenletet jelenti, melyet integrálva az

egyenlethez jutunk. Ennek megoldása:

,

amibõl egyszerûen következik a sugárfüggvény:

Ha a kúpvetületünk póluspontos (B=0  esetén  r=0), akkor a  d  integrációs konstanst a

egyenlet adja. Legyen most a  B_n  pólustávolságú parallekör hossztartó. Ekkor a

egyenletbõl kifejezhetõ az  n  sugárhajlás:

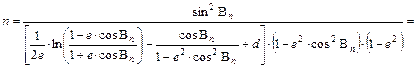
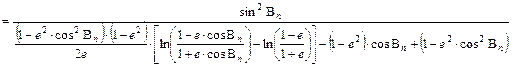
A  B_n hossztartó parallekör torzulásmentes.

A pólusvonalas területtartó kúpvetület lehet egy vagy két parallelkörben hossztartó.

Ha  B_n  az egyetlen hossztartó parallelkör, akkor a

egyenleten kívül fel kell még tételezni, hogy a  h  parallelkör menti hossztorzulás a  B=B_n  parallelkörön veszi fel a minimumát:

Az utóbbi egyenlõséget a

képletbõl részletesen felírva:

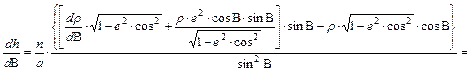
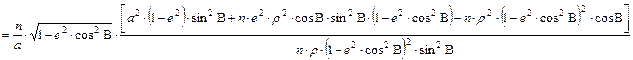
(ahol felhasználtuk a területtartás

egyenletét.)

Elvégezve a  B=B_n  behelyettesítést, az így kapott

egyenletbõl a  r²(B_n)-et kifejezve és ebbe beírva a területtartó kúpvetület fentiekben meghatározott  r  sugárfüggvényét, az alábbi egyenlethez jutunk:

Innen  d  kifejezhetõ:

Most térjünk vissza a hossztartás egyenletéhez, illetve annak négyzetéhez:

Helyettesítsük be  r²(B_n)  általános képletét, abba pedig  d  iménti értékét:

Az egyszerûsítések elvégzése után kapjuk, hogy

A területtartás miatt a hossztartó parallelkör egyben torzulásmentes.

A két (B₁ és  B₂)  parallelkörben hossztartó verzióban a  d és az  n  paramétert a

     és a     

egyenletekbõl határozzuk meg. Négyzetreemelés után:

és

Fejezzük ki  r²-e mind a két egyenletbõl:

és

Egyszerûsítés és átszorzás után a  d kiküszöbölése céljából vonjuk ki a két egyenletet egymásból

Fejezzük ki innen  n-t:

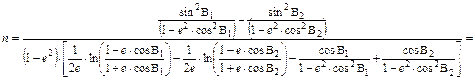
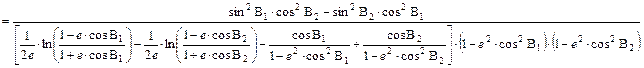
Ha a két fenti egyenletet elosztjuk egymással, akkor  n esik ki:

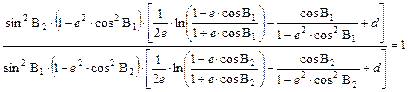
Innen kifejezhetõ  d:

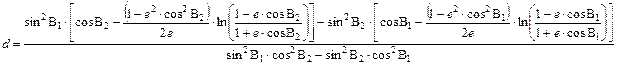Ez a nevezetes Albers féle területtartó kúpvetület ellipszoid alapfelületû változata. A két hossztartó parallelkör a területtartás miatt egyben torzulásmentes is. Elsõsorban az Egyesült Államokban használatos az egyes tagállamok nagyobb méretarányú geokartográfiai ábrázolásánál.

Az „Atlas der Donauländer” területtartó kúpvetülete

A Duna menti országok természet- és társadalomföldrajzi viszonyait  M = 1 milliós méretarányban  48 különbözõ tematikával ábrázoló, bécsi kiadású „Atlas der Donauländer” 1970 és 1989 között folyamatosan, térképlaponként jelent meg. A 48 térképlap egységes vetületben készült, amely a korábbiakban leírt ellipszoid alapfelületû póluspontos területtartó kúpvetület némileg egyszerûsített közelítése.

E vetületben az  n  sugárhajlást és a  r  sugárfüggvényt az alábbi képletek adják meg:

és

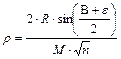
ahol az e  korrekciós tag képlete:

A vetület alapfelülete a nemzetközi Hayford-elliszoid. Az ábrázolt terület nagyjából a 39° és az 51° É-i szélesség között terül el. Ennek megfelelõen a  F_n=B_n=45°-os szélességet választották hossztartó parallelkörnek, amely a területtartás miatt torzulásmentes, továbbá

R=6374.2 km

az ábrázolt területre érvényes középgömb sugara.

Az ellipszoidi kétszög leképezései a topokartográfiában ún. transzverzális hengervetületekkel

A Cassini-Soldner vetület

Képezzünk le síkra egy ellipszoidi kétszöget úgy, hogy mind a középmeridián, mind az erre merõleges ortodrómák képe a középmeridián képére merõleges, hossztartó egyenes legyen. Ezen ortodrómák képei tehát a térképen párhuzamos egyenesekként jelennek meg. Válasszuk a középmeridián és az egyenlítõ egymásra merõleges képét a síkkoordináta x és y tengelyének (???ábra). Gömb alapfelület esetén egy meridiánra, mint segédegyenlítõre merõleges gömbi fõkörök (segédmeridiánok) a transzverzális négyzetes hengervetületben (a Cassini vetületben) párhuzamos egyenesként jelennek meg, és mind ezek, mind a segédegyenlítõ hossztartó. A Cassini-Soldner vetület ezek szerint a gömbi Cassini vetület ellipszoidi általánosításának tekinthetõ, ezért a valódi vetületek közé soroljuk.

Az ellipszoidi és a síkkoordináták közötti átszámítások visszavezethetõk a geodéziai alapfeladatokra. Legyen  L₀  az ellipszoidi kétszög középmeridiánja. A  P(F,L) ellipszoidi pontból kiinduló, a kezdõmeridiánra merõleges ortodróma talppontjának koordinátáit jelöljük P₀(F₀, L₀)-lal (???ábra). Ekkor a P pont azimutja 90° vagy 270°, a polártávolsága az  y  síkkordinátával egyezik meg, az egyenlítõtõl a  P₀  pontig terjedõ meridiánív hossza pedig éppen az  x  síkkoordináta. A P₀ pontot origónak véve, a P pontra vonatkozó elsõ és második geodéziai alapfeladat most két olyan egyenlet, amelyekben F₀  ismeretlen, az azimut pedig rögzített. Ezt kiegészítve a

egyenlettel egy olyan egyenletrendszerhez jutunk, amely alapján ismert térképi síkkoordinátákból földrajzi koordináták határozhatók meg, és fordítva.

Az explicit vetületi egyenletek a C. J. Mugnier által megadott sorfejtéses alakban a következõk:

Ez a vetület általános torzulású. A középmeridián torzulásmentes. A torzulások a középmeridiántól távolodva nõnek, ezért a vetület topográfiai célokra 3-4°-nál távolabb már nem használható. Elsõsorban egy meridián mentén hosszan elterülõ terület ábrázolására alkalmas.

A vetület alapgondolata a híres francia tudósdinasztiából származó C.-F. Cassini de Thury-tól ered. Az ellipszoidi képleteket J. G. von Soldner német matematikus dolgozta ki 1810-ben.

Ebben a vetületben készült a XVIII. század második felében Franciaország katonai térképe (Carte de France), majd Bajorországban és a Habsburg Monarchiában használták. A XIX. században több országban, így pl. Nagy-Britanniában, Itáliában, Norvégiában alkalmazták a topográfiai térképezéshez.

A Monarchia második katonai felmérésének vetülete, az ún. „vetület nélküli rendszer” lényegében a Cassini-Soldner vetületen alapult. A háromszögelési pontok síkkoordinátáit a kezdõpontokból kiinduló sokszögvonalak oldalainak meridián irányú és arra merõleges összetevõibõl számolták, a hosszakat redukció nélkül vitték át a síkra. Az ilyen módon kiszámított síkkoordináták értéke ezért függött az útvonaltól, nem volt egyértelmû. Innen ered a „vetület nélküli” elnevezés. A Monarchia területére bevezetett tíz koordinátarendszer közül három esett Magyarországra (a budai, a nagyszebeni és az Ivaniƒ-i). Késõbb az 1850-es években ebben a vetületben kezdõdött el az ország polgári célú, kataszteri térképezése.

A Gauss-Krüger vetület

A meridiánok összetartása miatt az alapfelület egy pontjában az azonos meridián- és parallelkör-irányú megváltozáshoz általában különbözõ szélesség- és hosszúság-megváltozás tartozik. A vetületek szögtartásának vizsgálatához célszerû bevezetni egy olyan újfajta szélességet, amelynél az ilyen egyenlõ hossz-megváltozásokhoz egyenlõ szögmegváltozások tartoznak. Ezeket a koordinátákat izometrikus koordinátáknak, a szélességet pedig  Y izometrikus szélességnek nevezzük. Összefüggését a földrajzi szélességgel gömbön a

,

ellipszoidon pedig a

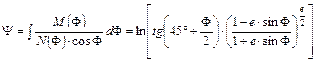
képlet adja meg.

A vetületek torzulási viszonyairól szóló fejezetben megállapítottuk, hogy szögtartó vetületeknél az  l_a  hossztorzulási modulus nem függ az iránytól, vagyis az  a  azimuttól. Írjuk fel  l_a²-et az ellipszoidon, izometrikus koordináták felhasználásával:

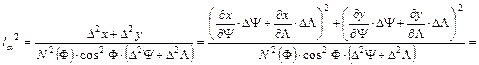
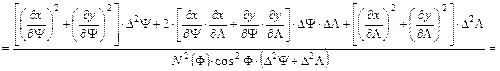
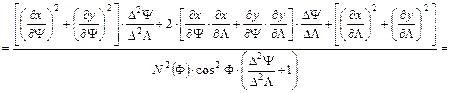
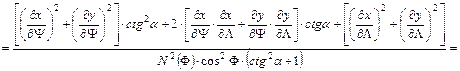
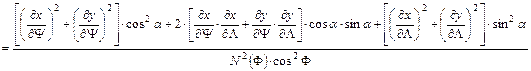
(Közben felhasználtuk a vetületi egyenletek folytonos differenciálhatóságát és az izometrikus szélesség definíciójából következõ

egyenlõséget.)

Ez a kifejezés akkor független az azimuttól, ha teljesül a

és egyszersmind a

egyenlõség.

A két egyenletbõl vagy a

   és   ,

vagy pedig a

   és  

egyenletek következnek. Ezek az ún. Cauchy-Riemann féle differenciálegyenletek, amelyek a komplex változós függvények elméletébõl ismertek.

A leképezés szögtartásából tehát következik, hogy ezen egyenletek teljesülnek az izometrikus koordináták parciális deriváltjaira. A gondolatmenet meg is fordítható: ha az izometrikus koordináták szerinti parciális deriváltak folytonosak, és teljesülnek a Cauchy-Riemann egyenletek, akkor a leképezés szögtartó.

Képezzünk most le egy ellipszoidi kétszöget a síkra szögtartó módon úgy, hogy a L₀ középmeridián képe egy hossztartó egyenes legyen. Ha a leképezést egy

alakú komplex függvénnyel valósítjuk meg, akkor a Cauchy-Riemann egyenletek teljesülése az  f  függvény sorbafejthetõségét biztosítja. A sorbafejtést végigszámolva és felhasználva a középmeridiánra tett feltételt, a valós és képzetes rész szétválasztása után az alábbi vetületi egyenleteket kapjuk:

ahol

és az  A₁, A₂, A₃, …, A₆, …  együtthatók a  F  geodéziai szélesség függvényében vannak megadva, többnyire az alábbi alakban:

 ,

és

.

Hasonló sorfejtés eredményeként jönnek ki az inverz vetületi egyenletek.

A Gauss-Krüger vetület gömb alapfelület esetén éppen a transzverzális elhelyezésû szögtartó (Mercator) hengervetületbe megy át, ezért a gömbi transzverzális Mercator vetület ellipszoidi általánosításának szokás tekinteni, így ezt a vetületet is a valódi vetületek közé soroljuk.

A származtatás miatt a középmeridián torzulásmentes. Ettõl távolodva a hossz- és területtorzulások növekednek. Topográfiai alkalmazáshoz ±3°-ig tekintik használhatónak, ami 6°-os zónaszélességet jelent. A geodéziai használatban 2°-os és 3°-os zónaszélességgel dolgoznak.

C. F. Gauss vizsgálatai alapján a geodéziailag is használható formulákat J. H. L. Krüger német matematikus és geodéta dolgozta ki 1912-ben. Alkalmazása Németországban és Ausztriában kezdõdött Bessel ellipszoid alapfelülettel. A Szovjetunióban a két világháború között Bessel ellipszoiddal, 1942 után Kraszovszkij ellipszoiddal használták. 1949 után ez utóbbi vezették be a szocialista országok a katonai topográfiai térképészetben, és még a 90-es években is használták.

Az UTM (Universe Transverse Mercator) vetület

Az UTM vetület a Gauss-Krüger vetület módosítása egy 0.9996-os redukciós együttható segítségével a torzulások csökkentése céljából. A vetületi egyenletek ezek szerint felírhatók az alábbi formában:

 ,

de a számítás pontosságának növelése érdekében más alakban is használatosak. A Gauss-Krüger vetülettel együtt összefoglalólag „transzverzális Mercator vetületek” néven is emlegetik, és többnyire szintén valódi vetületnek tekintik.

A vetület szögtartó, és két torzulásmentes vonala van a középmeridiánnal párhuzamosan. Ezek az egyenlítõt a középmeridiántól ±1° 37’ 15”-nyi távolságban metszik. A torzulásmentes vonalak között a hossz- és területtorzulási modulusok 1-nél kisebbek, ezeken kívül 1-nél nagyobbak, és a középmeridiántól távolodva növekednek. A határoló meridiánnál azonban a maximális torzulások kisebbek, mint a Gauss-Krüger vetületnél.

Az UTM vetületet az Egyesült Államok hadseregében fejlesztették ki az 1940-es években, és 1947-tõl rendszeresítették Hayford (1924) ellipszoid alapfelülettel. 1952-tõl lett a NATO térképek vetülete. Számos országban használják felmérési térképek vetületeként Clarke (1866) és Clarke (1880) ellipszoidon. A NATO térképeknél, így hazánkban is az utóbbi évtizedben a WGS’84 ellipszoid alapfelületre tértek át. E katonai topográfiai világtérképmû a Földet a 80° D-i szélességtõl a 84° É-i szélességig 6°-os zónákon ábrázolja UTM vetületben; a sarkokat ábrázoló térképek a már említett UPS vetületben készülnek.