A VETÜLETI TORZULÁSOK

A bevezetőben láttuk, hogy a térképen a hosszak torzulásával mindenképpen számolnunk kell. A térképhasználat során a hosszak mérésén kívül szükség lehet a szögek és a területek mérésére is. A térképi mérésekből csak a torzulások mértéke és eloszlása ismeretében tudunk megbízhatóan következtetni az alapfelületi mértékekre, ezért a torzulások meghatározása a vetülettanban központi szerepet játszik. Ehhez először pontosan definiálnunk kell a vetületi torzulások fogalmát.

A torzulási arányok

Torzulási arány alatt a véges nagyságú objektumok térképi és alapfelületi méretének arányát értjük. A hossztorzulási arány definiálásához vegyük egy mérhető hosszúságú alapfelületi vonal ívhosszát (s) és pontonként vetített képfelületi megfelelőjének s' ívhosszát. (A vetületi egyenletek tulajdonságaiból adódóan s' általában létezik.) Ekkor az l hossztorzulási arány:

A szögtorzulási arányhoz tekintsünk két, egymást metsző sima (törésmentes) görbét, és ezeknek képfelületi megfelelőit, amelyek a vetületi egyenletek tulajdonságaiból következőleg szintén egymást metszők és simák lesznek. Az egymást metsző vonalak által bezárt szög alatt a metszéspontbeli érintőik által bezárt szöget értjük. Legyen az érintők szöge az alapfelületen d, a képfelületen d'. Ekkor az i szögtorzulási arány:

Első irányredukciónak nevezzük az érintők alapfelületi és képfelületi szögének D^I=d-d' különbségét, vagyis a szög megváltozását a leképezés eredményeként.

A geodéziai vonal képe általában – néhány speciális vonaltól eltekintve – görbe vonal. Két pontot összekötő ilyen görbeív és a húr szögeltérését a végpontokban az ún. második irányredukcióval jellemezzük. A fogalom definíciójának megadásához szükség van a vizsgált O pontban egy kezdőirány megadására mind az alap-, mind pedig a képfelületen; ez rendszerint a pólus iránya, amelyet a meridián illetve a meridiánkép érintője ad meg. Vegyünk fel most a vizsgált ponton kívül egy tetszőleges P pontot az alapfelületen, melynek képe P’ (???ábra). Az O-t és P-t összekötő geodéziai vonal O’P’ képének az O’-beli érintője általában nem esik egybe az O’P’ egyenessel; az általuk bezárt szöget második irányredukciónak nevezzük. Ennek nagysága a vizsgált O pontban az O’-beli érintőn kívül függ a P helyétől is.

A területtorzulási arányt az alapfelületi idom F felszínének és a képe F’ területének alapján számíthatjuk az alábbi képlettel:

A torzulási modulusok

A torzulási modulusok a torzulásokat a térkép egyes pontjaiban jellemzik, melyeket ezért határértékként definiálunk. Ezt szokás úgy is kifejezni, hogy nem véges nagyságú, hanem „végtelen kicsiny” mennyiségekre vonatkoznak.

Tekintsünk az alapfelület P pontján áthaladó sima görbét és azon egy másik Q pontot, valamint ennek a P’-n és Q’-n áthaladó képét. Ha a Q pont a görbe mentén minden határon túl megközelíti P-t, akkor az Ds-sel jelölt PQ ívből és a Ds’-vel jelölt P’Q’ ívből a

képlet adja az l hossztorzulási modulust vagy lineármodulust.

A vetületi egyenletek tulajdonságaiból következőleg a P pontban fellépő hossztorzulási modulus nem függ attól, hogy a Q pont a P-t milyen görbe mentén közelíti meg, hanem csak a görbe P-beli érintőjének irányától. Ezt úgy is fogalmazhatjuk, hogy a hossztorzulási modulus általában a hely és az irány függvénye. Ha a hossztorzulási modulus a térkép egy pontjából kiinduló minden irányban egységnyi, vagy egy vonal mentén egységnyi, akkor hossztartó pontról vagy vonalról beszélünk.

A szögtorzulási modulus definíciója megegyezik a szögtorzulási arányéval, vagyis az egymást metsző görbék érintője által bezárt alapfelületi d és képfelületi d' szögekre vonatkozólag:

(A határátmenetet itt az érintők mint a szelők határhelyzetei képviselik.) Ha a térkép egy pontjában bármely irányok különbségére i=1 –nek adódik, akkor a térkép e pontban szögtartó. Ha a térkép minden pontjában szögtartás áll fent, akkor szögtartó vetületről beszélünk.

Vegyünk most egy P pontot tartalmazó, Df felszínű felületdarabot az alapfelületen, melynek képe egy Df’ területű idom lesz a képfelületen. Zsugorítsuk rá a P pontra az alapfelületi idomot úgy, hogy minden pontja egyenletesen konvergáljon P-hez, miközben Df®0. Ha a

határérték létezik, akkor ezt nevezzük a területtorzulási vagy területi modulusnak. Ha a térkép egy pontjában t=1, akkor a térkép e pontban területtartó. Ha a térkép minden pontjában területtartás áll fent, akkor a vetületet területtartónak nevezzük.

A vetületek tehát a torzulásaik alapján lehetnek, szögtartók, lehetnek területtartók, de – amint azt a későbbiekben látni fogjuk – nem lehetnek egyidejűleg szögtartók és területtartók is. E két nagy torzulási csoporton kívül vannak még olyan vetületek, amelyeknél mind a szögek, mind a területek torzulhatnak; ezeket általános torzulásúaknak nevezzük.

Torzulásmentességről akkor beszélünk, ha a térkép valamely pontjában vagy valamely vonala mentén semmilyen torzulás sem lép fel, vagyis mind a hossztartás, mind a szög- és területtartás fennáll.

A hossztorzulás vizsgálata

Tekintsünk az alapfelületen a P(j,l) pontot, és a koordinátáinak kismértékű megváltoztatásával keletkezett P_D(j+Dj,l+Dl) pontot, melyeket összekötő ortodrómaív hosszát Ds jelöli (???ábra), továbbá az ortodrómaívnek a l meridiánnal bezárt szöge (az azimut) legyen α. Képezzük le az így keletkezett kis foktrapézt az x,y síkba. A P pont képét jelölje P’, a P_D-ét P_D’, az ortodrómaív képének hosszát Ds’. A kis foktrapézt és képét közelítőleg síkban lévőnek tekintve írjuk fel az α azimut irányába fellépő P pontbeli lineármodulus négyzetét az R sugarú gömbön:

illetve a forgási ellipszoidon:

Itt felhasználtuk, hogy a kis foktrapéz közelítőleg téglalapnak tekinthető. A vetületi egyenletek tulajdonságai miatt a foktrapéz oldalai közelítőleg egyenes szakaszokra képeződnek le, így a képfelületi idom közelítőleg négyszög lesz.

Írjuk fel a Dj szélességmegváltozás és a Dl hosszúságmegváltozás eredményeként bekövetkezett Dx és Dy térképi koordinátaváltozásokat:

Hasonlóan kapjuk:

(Mindkét képletben felhasználtuk a vetületi egyenletek folytonos differenciálhatóságát.) A Dx és Dy síkkoordináta-megváltozások tehát lokálisan a Dj és Dl földrajzi koordináta-megváltozások lineáris függvényei. Ezekből a képletekből, amelyeket a (???) ábra szemléltet, látható, hogy mind Dx, mind Dy egy (előjeles) parallelkör irányú és egy (ugyancsak előjeles) meridián irányú megváltozásból adódik össze, amelyek a négyszög egy-egy oldalának a koordinátatengelyeken jelentkező merőleges vetületei. A szemközti oldalak közelítőleg egyenlő hosszúságúak, emiatt a foktrapéz képe közelítőleg parallelogramma.

Helyettesítsük be l_α² képletébe az így kapott

és

egyenlőségeket a gömbön:

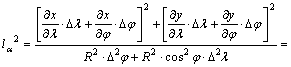
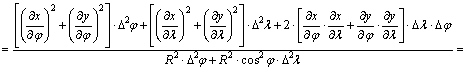
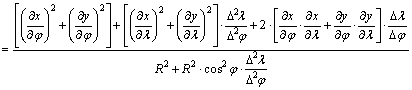
(Ez és az itt következők kis változtatással ellipszoid alapfelületre is átvihetők, de a folytatásban gömb alapfelületre korlátozódunk.)

A közelítőleg téglalapnak tekintett kis foktrapézról leolvasható, hogy

Innen kapjuk, hogy

Ezt behelyettesítve l_α² képletébe:

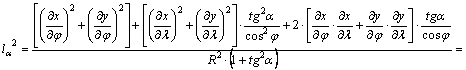
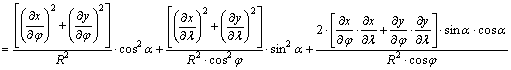
A hossztorzulási modulus tehát (a parciális deriváltakon keresztül is) a P pont koordinátáitól és az α azimuttól függ, vagyis általában a hely és az irány függvénye.

Ha α=0°, akkor l_α a meridián mentén fellépő (k-val jelölt) hossztorzulást adja:

,

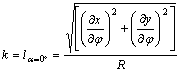míg α=90° esetén a parallelkör menti (h-val jelölt) hossztorzulást kapjuk:

.

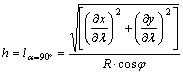Vizsgáljuk most a lineármodulust szögtartó vetületek esetén. Ehhez képezzük le az ABC kicsiny gömbháromszöget az A’B’C’ síkháromszögre (???ábra) szögtartó módon. Az ABC gömbháromszög közelítőleg síkháromszögnek tekinthető, és a szögek egyenlősége miatt hasonló lesz az A’B’C’ háromszöghöz. Ekkor a háromszögek megfelelő oldalainak arányai megegyeznek:

,

átrendezve

,

és a tetszőleges D pont által meghatározott ADB gömbháromszögre ugyanilyen módon kapjuk, hogy

Ezek a hányadosok közelítőleg az A pontban a különböző irányokba fellépő l_A lineár-modulusokat adják meg:

,

következésképpen tetszőleges irányokra a lineármodulus megegyezik. Másként fogalmazva: a szögtartó vetületeknél a lineármodulus csak a helytől függ, az iránytól nem. (Ez a gondolatmenet meg is fordítható, azaz ha egy leképezés minden pontjában a lineármodulus az iránytól független, akkor a vetület szögtartó.)

A megállapításunk tetszőleges sima felületek közti szögtartó leképezésre érvényes, így pl. az ellipszoidot a gömbre leképező szögtartó gömbvetületre is.

A fokhálózat szögének torzulása

Az alapfelületen a meridiánok a parallelkörökkel – gömbön és ellipszoidon egyaránt – derékszöget zárnak be. A térképen egy fokhálózati metszéspontban négy szög keletkezik, ezek közül kettő-kettő váltószög és így egyenlő, a szomszédos szögek pedig 180°-ra egészítik ki egymást. A szögérték helyett ezért inkább egy olyan mennyiség volna hasznos, amely a szög 90°-tól való eltérését jellemzi, és így mind a négy szögre ugyanazt az értéket adja. Erre a célra megfelel a szög kotangense, amely 90°-nál zérus, és annál nagyobb, minél jobban eltér a metszésponti szög a derékszögtől.

Jelöljük a fokhálózati vonalak képei által bezárt valamelyik szöget Q-val, és írjuk fel azon J_p’ és J_m’ irányszögek különbségeként, amelyek a parallelogramma két oldala és az x tengellyel párhuzamos egyenes között keletkeznek (???ábra). Ekkor

Az ábra alapján a parallelogramma oldalairól és ezek x és y tengely irányú összetevőiről leolvashatók az alábbi összefüggések:

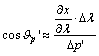
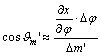
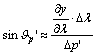
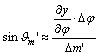
Ezeket behelyettesítve kapjuk ctgQ-ra Dj®0, Dl®0 esetén:

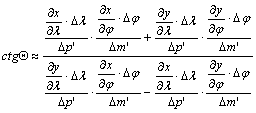
Egyszerűsítés és határátmenet után kapjuk ctgQ-t:

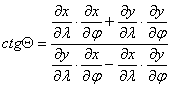
A fokhálózat torzulásait tehát a parallelkör menti h hossztorzulás, a meridián menti k hossztorzulás és a fokhálózati vonalak által bezárt Q szög kotangense együttesen jellemzi.

A területtorzulás

A fokhálózat torzulásai alapján – az alapfelületi kis foktrapéz DT felszíne és a képfelületi kis parallelogramma DT’ területe segítségével – felírható a t területtorzulási modulus. Írjuk fel a parallelogramma területét:

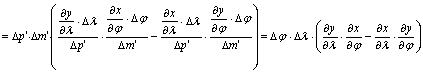
A foktrapéz területe:

Írjuk fel ezek hányadosát:

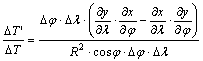
Egyszerűsítés és határátmenet után kapjuk a t területtorzulási modulust:

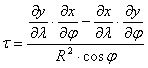
A vetületi főirányok

Keressük az l_α lineármodulus szélsőértékeit, amely ott lehet, ahol

.

Ugyanitt a lineármodulus négyzetének is szélsőértéke van, mert

.

A fenti képletből:

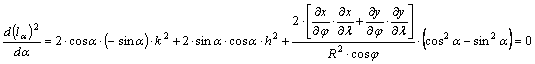
Innen

.

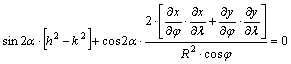Ezt átrendezve:

.

A tangens-függvény periodicitásából következik, hogy ha 2α gyöke az egyenletnek, akkor 2α±180° is gyök; emiatt ha α gyök, akkor α±90° is gyök. A két irány közül az egyik a lineármodulus maximumának, a másik a minimumának iránya.

Azokat az alapfelületen egymásra merőleges irányokat, amelyek a linármodulus szélsőértékeinek irányai, vetületi főirányoknak nevezzük. A maximális lineármodulus iránya az I. vetületi főirány, a minimális lineármodulus a II. vetületi főirány.

Tissot torzulási elmélete

A vetületi torzulások manapság elfogadott elmélete Nicolas August Tissot francia matematikus 1881-ben megjelent összefoglaló munkája alapján terjedt el. A Tissot elmélet első fontos megállapítása, hogy bármely vetület közelítőleg előállítható egy kicsiny elemi részekre felosztott alapfelület elemenkénti ortogonális leképezéseinek együtteseként, ahol ezeknek az ortogonális elem-képeknek elemenként változó lehet a méretaránya (???ábra). Tissot ezt egy alapfelületi elemi kis kör leképezésével szemléltette, amely állítása szerint a térképen – egy merőleges affinitás és egy hasonlósági transzformáció együttes végrehajtása eredményeként – egy elemi kis ellipszis lesz; ezt nevezhetjük Tissot első tételének.

Az állítás igazolásához vegyünk egy Ds sugarú kis kört az alapfelületen a P pont körül (???ábra). Ennek kanonikus egyenlete:

Térjünk át a képsíkra oly módon, hogy behelyettesítjük Dj-be és Dl-ba ezek Dx-től és Dy-tól függő képleteit, amelyeket a fenti, a vetületi egyenletek folytonos differenciálhatóságából adódó és lokálisan érvényes

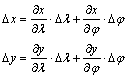
lineáris egyenletrendszer megoldásából kapunk:

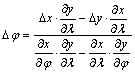
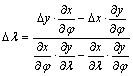
A behelyettesítés eredményeként egy síkbeli alakzat egyenletét kapjuk:

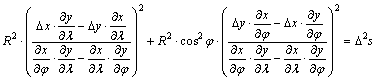
A négyzetreemelés, a nevezővel való átszorzás és átrendezés után:

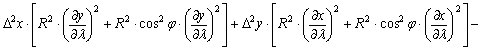
Vegyük észre, hogy egy konkrét vetület esetén egy konkrét pontban a tagok együtthatói konstansok. Vezessük be ezekre a

jelöléseket. Így az alakzat egyenlete:

Erről az egyenletről szeretnénk látni, hogy egy olyan ellipszis egyenlete, amelynek tengelyei nem szükségszerűen párhuzamosak az x,y tengelyekkel.

Tudjuk, hogy az a,b féltengelyű ellipszis kanonikus egyenlete a Dx, Dy koordinátarendszerben:

Ugyanezen ellipszis egyenlete az origó körüli e szöggel való elforgatás után (???ábra):

ahol a Dx’, Dy’ tengelyek a Dx, Dy tengelyek e szöggel való elforgatásából keletkeztek, amely az alábbi mátrixszorzással valósítható meg:

A behelyettesítés után a kanonikus egyenlet alakja:

Átrendezés után kapjuk az elforgatott ellipszis egyenletére, hogy

Ha a fenti alakzatunk egyenlete ilyen alakú (vagyis a megfelelő együtthatók egyenlők), akkor valóban egy ellipszis egyenlete. Teljesülnie kell tehát a

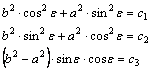
egyenletrendszernek.

Az első egyenletből kivonva a másodikat kapjuk, hogy

Innen kifejezzük (b²–a²) –et, és behelyettesítjük a harmadik egyenletbe:

Innen

A baloldali törtet -nal bővítve:

Ez tge-ra nézve másodfokú egyenlet:

Az egyenlet gyökei:

A diszkrimináns négyzetösszeg, ezért az egyenletnek mindig van megoldása. Ha (tge₁) és (tge₂) a két megoldás, akkor

vagyis az e₁ és e₂ szögek 90°-ban különböznek egymástól.

A harmadik egyenletet a két első egyenlet összegével összeadva, illetve abból kivonva, kapjuk, hogy

és

.

Könnyen belátható, hogy az egyenletek jobb oldalán mindig pozitív mennyiség áll, így az eredeti egyenletrendszerünknek mindig van valós e, a, b megoldása.

e₁ és e₂ behelyettesítése mind b²-re, mind a²-re két megoldást ad, de

miatt

és .

A két lehetséges megoldásrendszer közül válasszuk azt, amelynél

,

vagyis az ellipszis nagy féltengelye a Dx’ irányába mutat.

A fentiek azt mutatják, hogy mindig van két olyan, egymással derékszöget bezáró Dx’, Dy’ irány, amelyekbe elforgatva a Dx, Dy tengelyeket, a fenti alakzat egyenlete egy ellipszis

alakú kanonikus egyenletébe megy át. Ezt az ellipszist torzulási ellipszisnek vagy Tissot-indikatrixnak nevezik.

Szemléletesen demonstrálni fogjuk, hogy az alapfelületi kicsiny kört a képfelületi kicsiny ellipszisbe átvivő leképezés előállítható egy olyan transzformációval, amely egy a/Ds –szeres hasonlósági transzformációból és egy b/a arányú merőleges affinitásból tevődik össze. Ehhez tekintsük a P középpontú, Ds sugarú alapfelületi kicsiny kör egyenletét:

Ugyanennek a körnek az egyenlete egy olyan P középpontú (közelítő) síkkorrdináta-rendszerben, melynek x tengelye az I., h tengelye pedig a II. vetületi főirány:

Hajtsunk végre egy a/Ds –szeres hasonlósági transzformációt erre a körre; ekkor a Ds sugarú kör egy a sugarú körbe megy át, melynek egyenlete:

A következő lépésben hajtsunk végre egy b/a-szoros merőleges affinitást az h tengely irányában; ennek eredményeként egy a nagy-féltengelyű, b kis-féltengelyű ellipszist kapunk az alábbi egyenlettel:

Helyezzük most egymásra a vetületi főirányok által definiált alapfelületi és a képfelületi síkkoordinátarendszert úgy, hogy a x tengely a Dx’ tengellyel, az h tengely pedig a Dy’ tengellyel essen egybe (???ábra). Az utóbbi ellipszis egybeesik a képfelületi,

egyenletű ellipszissel, amely mellesleg paraméteres alakban is felírható a xºDx’ tengelytől indított J paraméter segítségével:

Ezzel Tissot első tételét maradéktalanul beláttuk.

A közös síkkoordinátarendszerben felírhatók a következő egyenlőségek:

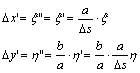
Az alapfelületi kicsiny kör Ds sugarát itt és a továbbiakban az általánosság megszorítása nélkül egységnyinek tekintjük. Ekkor a

összefüggéseket kapjuk.

Tissot második tétele

Az O középpontú, egységsugarúnak (Ds=1) tekintett alapfelületi kicsiny kör kerületén lévő P pont az O’ középpontú kicsiny ellipszis kerületének P’ pontjára képeződik le (???ábra). Az OP irány x tengellyel bezárt szögét J -val jelölve, írjuk fel az OP irányban fellépő l lineármodulus négyzetét a J paraméter függvényében:

Az alapfelületen a x tengellyel, vagyis az I. vetületi főiránnyal J szöget bezáró irányba fellépő l_J lineármodulust tehát az

képlet adja meg.

Könnyen belátható, hogy ha

,

akkor a lineármodulus maximuma J=0°±180°-nál , vagyis a torzulási ellipszis nagytengelyének irányában adódik, és

;

a lineármodulus minimuma pedig J=90°±180°-nál, vagyis a torzulási ellipszis kistengelyének irányában lép fel, és

.

A vetületi főirányoknak eddig az alapfelületen a hossztorzulás maximumának és minimumának irányait neveztük. Ezt az elnevezést most a képfelületre is kiterjesztjük, ahol is I. vetületi főiránynak a maximális hossztorzulás térképi irányát, II. vetületi főiránynak pedig a minimális hossztorzulás térképi irányát nevezzük. Eljutottunk továbbá Tissot második megállapításához, mely szerint a vetületi főirányok mind az alapfelületen, mind pedig a képfelületen merőlegesek egymásra. (Ez végső soron onnan ered, hogy a végrehajtott hasonlósági és affinitási transzformációk az affinitás tengelyirányát és az erre merőleges irányt nem változtatták meg.)

Szögtartó vetületek (a=b) esetén minden irányt vetületi főiránynak tekintünk.

A szögtorzulás. Tissot III. tétele

Tekintsük az alapfelületi egységsugarú kicsiny kör kerületi P pontjához tartozó J középponti szöget, amelynek másik szára az I. vetületi főiránnyal (x tengely) esik egybe. Ennek síkbeli képe a P’ pont és az általa meghatározott J’ szög, amelynek másik szára az I. vetületi főirány képére (Dx’ tengely) esik (???ábra). A J szög i_J szögtorzulási modulusa az ábráról leolvashatóan:

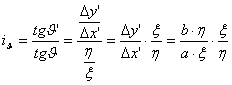
(Felhasználtuk a x,h és a Dx’,Dy’ síkkoordinátarendszerek egymásra helyezéséből adódó fenti összefüggésünket.) Innen egyszerűsítés után kapjuk:

Tissot III. tétele kimondja tehát, hogy ha egy szög egyik szára az I. vetületi főirányba mutat, akkor a szögtorzulási modulusa b/a. A tétel segítségével az alapfelületi J szögből a torzulási ellipszis a,b féltengelyeinek ismeretében kiszámítható J’:

Ha az alapfelületi J szög egyik szára sem esik egybe az I. vetületi főiránnyal, akkor felírjuk két ilyen típusú szög különbségeként:

Külön-külön alkalmazva Tissot III. tételét m-re és n-re, kapjuk a J szög első irányredukciójára, hogy

és ezek segítségével már adódik J’:

.

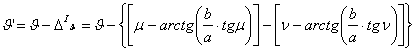Itt felhasználtuk, hogy bármely d szög D^I_d első irányredukciója:

A maximális szögmegváltozás („maximális szögtorzulás”)

A J szögnek a leképezés következtében fellépő megváltozása jellemezhető a

első irányredukcióval.

Vizsgáljuk a térkép egy O pontjában keletkezett szögmegváltozás mint függvény viselkedését. Ehhez ismét helyezzük egymásra a x,h és a Dx’,Dy’ síkkoordinátarendszereket, és vegyük fel megint az egységsugarú kicsiny kör kerületén a P pontot a hozzá tartozó J középponti szöggel, amelynek másik szára az I. vetületi főiránnyal (xºDx’ tengely) esik egybe (???ábra). Ha a J szöget folytonosan növeljük 0°-tól 90°-ig, akkor a D^I_J mennyiség 0-ról indulva egy ideig növekszik, majd 90°-nál ismét zérussá válik a vetületi főirányok merőlegessége miatt. A folytonosság következtében a D^I_J függvény 0° és 90° között valahol felveszi a maximumát. Meghatározandó most e maximum helye és értéke.

A P(x,h) pontra végrehajtva az O origó-középpontú a-szoros hasonlósági transzformációt, az a sugarú kör kerületén lévő P_a(a×x, a×h) ponthoz jutunk, majd az h(ºDy’) tengely irányú b/a-szoros merőleges affinitás után kapjuk az ellipszoid kerületi P’(a×x, b×h) pontot. Az OP_aP’ háromszög O csúcsánál lévő szöge J -J ’, a P_a csúcsnál lévő szöget jelöljük e-nal. E háromszögben írjuk fel a szinusztételt:

ahol l a vizsgált irányba fellépő lineármodulus. Tükrözzük most a P_a csúcsot a x(ºDx’) tengelyre, így kapjuk a Q_a pontot. Az OP’Q_a háromszög O csúcsnál lévő szöge J +J ’, a Q_a csúcsnál lévő szög a tükrözés miatt e. E háromszögben a szinusztétel:

Osszuk el egymással ezt a két egyenletet:

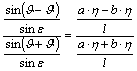
Egyszerűsítés után:

Kifejezve innen sin(J -J ’) -t:

A J -J ’ (hegyesszög) és a sin(J -J ’) ugyanazon J -nál veszi fel a maximumát, utóbbinak pedig ott lehet maximuma, ahol a jobboldali kifejezésben a sin(J +J ’) –nek. A szinusz-függvény 90°-nál veszi fel a maximumát, tehát amikor J +J’=90°, és itt a függvényérték egységnyi. Tehát

Az első irányredukció maximumára bevezetve az w= D^I_max=J -J ’ _max jelölést:

Jelöljük a maximális első irányredukciót elszenvedő szöget J_m –mel, a térképi megfelelőjét J ’_m –mel. Ekkor J_m+J ’_m=90° miatt

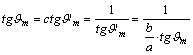
Innen következik, hogy

Másrészt

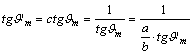
következésképpen

Ha a kérdéses O pontban az I. vetületi főiránnyal J_m szöget bezáró irány torzul a legnagyobb mértékben, akkor az O pontban találkozó szögszárak által bezárt szögek közül nyilván az torzul a leginkább, amelynek szárai az I. vetületi főirányra szimmetrikusak, és külön-külön J_m szöget zárnak be azzal. E 2×J_m nagyságú szög redukciója a korábbi w mennyiség kétszerese lesz, vagyis

.

Ez tehát az O pontban fellépő szögredukciók maximuma, amit maximális szögtorzulásnak is szoktak nevezni.

Összefüggések a fokhálózat torzulásai és a lineármodulus szélsőértékei (a torzulási ellipszis méretei) között

Egy tetszőleges térképi pontban fellépő fokhálózati torzulások: a h parallelkör menti és a k meridián menti hossztorzulás, valamint a fokhálózati vonalak által bezárt Q szög együttesen meghatározzák a pontban fellépő hossztorzulások a maximumát és b minimumát, vagyis a torzulási ellipszis féltengelyeit. Az összefüggések megkapásához vegyük fel az alapfelületet közelítő és a vetületi főirányok által kijelölt x,h síkkoordináta-rendszerben az origó-középpontú, egységsugarúnak tekintett alapfelületi kicsiny kört, valamint képét, a kis ellipszist a térképi Dx’,Dy’ koordinátarendszerben, melynek origója az ellipszis középpontja, tengelyei pedig egybeesnek az ellipszis tengelyeivel (???ábra).

Az ellipszis középpontját a kerületi pontokkal összekötő egyenes szakaszok közül azok, amelyek az origón átmenő fokhálózati vonalak képeire esnek, közelítőleg megegyeznek a h parallelkör menti és a k meridián menti hossztorzulással. Vezessük be a kerületi pontok alapfelületi közelítő síkkoordinátáira a x_p,h_p, ill. x_m,h_m’, a térképi síkkoordinátáira az Dx_p’, Dy_p’, ill. Dx_m’, Dy_m’ jelölést, és jelöljük a fokhálózati vonalak x tengellyel bezárt szögét u-val és v-vel, ezek képét pedig u’-vel és v’-vel. (Természetesen u+v=90° és u’+v’=Q.) Írjuk fel most h-ra és k-ra a Pythagoras tételt, figyelembe véve a

egyenlőségeket (ahol a és b a torzulási ellipszis kis és nagy féltengelye):

(Az utolsó egyenlőségnél felhasználtuk, hogy u és v merőleges szárú szögek.)

Adjuk össze a két egyenlőséget, és kapunk egyrészt h és k, másrészt a és b között egy összefüggést:

A fokhálózati vonalak képe által bezárt Q=u’-v’ szög szinusza (???ábra):

Átszorozva h×k -val:

(Kiküszöböltük az m indexet annak felhasználásával, hogy és , mert u és v merőleges szárú szögek.) Ezzel egy új összefüggéshez jutottunk egyrészt h és k, másrészt a, b és Q között.

Az

és

összefüggésekből meghatározható a és b. Az első egyenlethez hozzáadva ill. levonva a második egyenlet kétszeresét, kapjuk, hogy:

ill.

Vonjunk gyököt mindkét egyenletből:

Ezeket összeadva ill. kivonva, végül 2-vel osztva kapjuk, hogy:

Három független mennyiségből, a fokhálózat torzulásaiból így kaptuk a torzulási ellipszis méretét megadó a és b féltengelyt. A torzulási ellipszis harmadik jellemzőjéhez, a fokhálózathoz viszonyított állásához az alábbi módon jutunk.

Figyelembe véve, hogy u és v, valamint u’ és v’ a fokhálózati vonalaknak az I. vetületi főiránnyal bezárt szögei, ezért alkalmazható h-ra és k-ra az I. vetületi főiránnyal J szöget bezáró irányba fellépő l_J lineármodulus

képlete:

Hasonlóan (figyelembe véve, hogy u+v=90°)

Mindkét képletből kifejezhető sin²u:

Azonos gondolatmenet alapján kapjuk cos²u-t:

Most mindkettőből kifejezhetjük cos²u-t:

Ezeket egymással elosztva és gyököt vonva kapjuk a legalkalmasabb képleteket tg u-ra:

Analóg módon kapjuk a tg v-re vonatkozó képleteket:

Az alapfelületen u (vagy v=90°-u) a parallelkör vagy a meridián irányának ismeretében ki tudjuk jelölni az I. vetületi főirányt.

Alkalmazzuk u-ra és v-re Tissot harmadik tételét, mely szerint az első vetületi főiránnyal az alapfelületen J, a képfelületen J’ szöget bezáró irányra teljesül a

egyenlőség:

és .

A térképen u’ (vagy v’=Q–u’) ismeretében a fokhálózati vonalak irányához felmért szögek alapján ki tudjuk jelölni az első vetületi főirányt.

Összefüggések a vetületi torzulások és a lineármodulus szélsőértékei (a torzulási ellipszis méretei) között

Területtorzulás, területtartás

A t területtorzulási modulus felírható a torzulási ellipszis és annak ősképe, az (egységsugarúnak tekintett) kicsiny kör területének arányaként:

Tehát

illetve a fokhálózat torzulásainak segítségével:

A térkép egy pontjában a területtartás fennállása azt jelenti, hogy

vagyis a torzulási ellipszis két féltengelyének hossza egymásnak reciproka:

A vetület területtartó, ha minden pontban teljesül a területtartás iménti egyenlete.

Hossztorzulás, hossztartás

Láttuk, hogy a térkép egy pontjában a hossztorzulás függ az iránytól. A korábbiak szerint az I. vetületi főiránnyal J szöget bezáró irányban az l lineármodulus az

képletből kapható.

A térkép egy pontjában valamely irány menti hossztartás az

egyenlet teljesülését jelenti. Ha ennek az egyenletnek van egy J megoldása, akkor a torzulási ellipszis kétszeres szimmetriája miatt ennek -J ellentettje, valamint a ±(180°-J) is megoldás (???ábra). Nem állhat fenn hossztartás abban a pontban, amelyben teljesül a<1 vagy b>1.

Egy pontban iránytól függetlenül hossztartás áll fenn, ha

.

Szögtorzulás, szögtartás

Egy általános helyzetű J szög i szögtorzulási modulusa (felhasználva a J szög első irányredukciójának képletét):

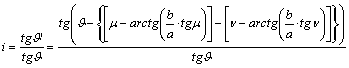
(ahol J=m-n , és mind m, mind n egyik szára az első vetületi főiránnyal esik egybe). Amennyiben J egyik szára az első vetületi főiránnyal egybeesik (vagyis m=J és n=0°), akkor a képletünk Tissot harmadik tételévé egyszerűsödik:

Ha a térkép egy pontjában szögtartás áll fenn, azaz minden szög szögtorzulási modulusa egységnyi, akkor ez a speciális J szögekre is igaz, következésképpen

vagyis

A szögtartó pontokban tehát a torzulási ellipszis körbe megy át.

A vetületet szögtartó, ha minden pontban teljesül a szögtartás iménti egyenlete.

Megjegyezzük, hogy a szögtartásnak szükséges, de nem elégséges feltétele a térképi fokhálózat merőlegessége (ortogonalitása). A térkép fokhálózata ortogonális, ha minden pontjában a fokhálózati vonalak által bezárt Q szög derékszög, azaz

,

tehát a vetületi egyenletekre teljesül a

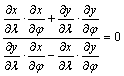
egyenlőség.

Torzulásmentesség

Ha a térkép egy pontjában teljesül mind a szögtartás (képletben

),

mind a területtartás (képletben

) ,

akkor ezekből

következik, ami az iránytól független hossztartást jelenti. Fordítva: egy pontban az iránytól független hossztartás egyben szögtartást és területtartást is eredményez. Az ilyen pontot torzulásmentesnek nevezzük.

Az eddigiekből kimutatható, hogy egy vetület nem lehet egyidejűleg szögtartó és területtartó, mert ez azzal járna, hogy a vetület minden pontban és minden irányban hossztartó volna, amit korábban már kizártunk. A vetületek tehát torzulási szempontból vagy szögtartók, vagy területtartók, vagy általános torzulásúak. A térképen viszont lehetnek olyan pontok vagy vonalak, amelyek torzulásmentesek, ezeket torzulásmentes helyeknek nevezzük, és a térkép vetületének fontos jellemzői.

A vetületi torzulások kiszámítása

Az eddigi eredményeink alapján a térkép bármely pontjában kiszámíthatók a vetületi torzulások, ha ismerjük az

vetületi egyenleteket. A legegyszerűbben a torzulási ellipszis a, b féltengelyein keresztül juthatunk el a torzulásokhoz.

Induljunk ki a vizsgált P pont j_P,l_P koordinátáiból. Határozzuk meg e pontban a vetületi egyenlet parciális differenciálhányadosait, azaz a

mennyiségeket.

A következő lépésben számítsuk ki a fokhálózat torzulásait a parciális differenciálhányadosok segítségével. A j_P parallelkör menti h hossztorzulás a l_P hosszúságon:

;

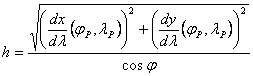a l_P meridián menti k hossztorzulás a j_P szélességen:

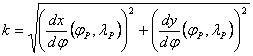
a j_P parallelkör és a l_P meridián által bezárt Q szög kotangense:

A cgtQ -ból kapjuk sinQ -t:

A fokhálózat torzulásaiból következnek a torzulási ellipszis a, b féltengelyei:

Végül a és b adja a torzulásokat.

A t területtorzulási modulus a P pontban:

Az l lineármodulus a P pontban, az alapfelületen az első vetületi főiránnyal J szöget bezáró irányban:

A P pontbeli szögtorzulás a két szögszár irányától is függ, ezért ennek mértékét egyszerűbb, irányfüggetlen mérőszámokkal adjuk meg. Ilyen pl a

hányados, vagy még inkább a

maximális szögmegváltozás.

Ha csak a területtorzulást szeretnénk meghatározni, akkor ehhez nincs feltétlenül szükség az a és b féltengelyekre; t kiszámítható a fokhálózati torzulásokból:

,

sőt közvetlenül a parciális differenciálhányadosokból is:

.
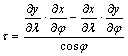