Valódi hengervetületek

Valódi hengervetületnek azokat a leképezéseket nevezzük, amelyek fokhálózata (vagy segédfokhálózata) rendelkezik az alábbi tulajdonságokkal:

- a (segéd-) parallelkörök képei párhuzamos egyenesek,

- a (segéd-) meridiánok képei párhuzamos egyenesek,

- a (segéd-) meridiánok képei a (segéd-) parallelkörök képeit merőlegesen metszik,

- a (segéd-) meridiánok képének távolsága arányos a (segéd-) hosszúságkülönbséggel.

Egy tetszőleges (j,l) koordinátájú alapfelületi pont képfelületi megfelelőjének síkkoordinátáit az

vetületi egyenletek adják meg. Az y a j-nek szigorúan monoton növő, és – kevés kivételtől eltekintve – páratlan függvénye, vagyis ebben az esetben az x tengely (az egyenlítő képe) a fokhálózat szimmetriatengelye. Az x vetületi egyenletben szereplő d integrációs konstans lehet zérus (ekkor az y tengely – a fokhálózat másik szimmetriatengelye – a kezdőmeridián képe lesz); d¹0 esetén az y tengely a l₀ középmeridián képére kerül. A vetületi kezdőpont tehát hengervetületeknél többnyire a (segéd-) egyenlítő és a (segéd-) kezdő- vagy a középmeridián metszéspontjában van. Előfordul ugyanakkor időnként egyik vagy mindkét koordinátatengely önmagával párhuzamos eltolása abból a célból, hogy a tévesztés lehetőségét magába foglaló negatív koordinátaértékeket elkerüljük.

A fokhálózat menti hossztorzulások:

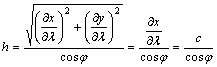
A c konstans értéke egyenlő a hossztartó parallelkör sugarának hosszával, ezért meghatározza annak helyét. Ha az egyenlítőt választjuk hossztartónak, akkor c=1; ha viszont a ±j_n szélességi kör hossztartó, akkor c=cosj_n. c>1 esetén nincs hossztartó parallelkör. Tehát

,

és

(Látható, hogy a fokhálózat menti hossztorzulások itt sem függnek l-tól.) A fokhálózati vonalak a képfelületi merőlegességük miatt vetületi főirányok, ezért az a és b extremális hossztorzulások közül az egyik h-val, a másik k-val fog megegyezni. Ezekből kapható meg a területi modulus:

illetve a térkép valamely pontjában fellépő 2w=2×D^I_max maximális szögtorzulás:

Perspektív hengervetületek

A vetületi egyenletek meghatározásához: messe a képfelület a ±j_n szélességi körön a gömböt, és legyen a vetítés középpontja a forgáshenger valamely Q pontjában, amely a leképezés egyrétűsége miatt nem lehet a gömbön kívül (???ábra). Tartalmazza az ábra síkja a forgástengelyt és a leképezendő (j szélességű) alapfelületi P pontot, így annak P’ képét is.

Az y vetületi egyenlet a P’ pontnak az egyenlítő képétől mért távolsága lesz. Jelölje E az egyenlítőnek az ábra síkjába eső egyik pontját; ennek képe, a QE egyenes E’ döféspontja – az egyenlítői pont képe – szintén az ábra síkjában van. O-val jelölve az alapfelület középpontját és G-vel az E’-ből a forgástengelyre bocsátott merőleges talppontját, kapjuk a hasonló QOE és QGE’ háromszögeket. A megfelelő befogók arányának egyenlőségéből.

.

Jelölje f=QO a vetítési középpont és a gömbközéppont távolságát (½f½£1). Felhasználva, hogy OE az egységnyinek tekintett gömbsugár, GE’ pedig a henger sugara, ami a metsző parallelkör cosj_n sugarával egyenlő, kapjuk, hogy

Képezzük most le az alapfelületi P pontot a QP vetítősugár segítségével a képfelületen lévő P’ döféspontra. F-fel jelölve a P pont, F’-vel a P’ pont merőleges talppontját a forgástengelyen, a kapott QFP és QF’P’ hasonló háromszögek megfelelő befogóinak arányára:

.

Felhasználva, hogy F’P’ szintén a henger sugara, tehát egyenlő cosj_n -nel, továbbá

(a P pont szélességi körének sugara),

,

kapjuk, hogy

Másrészt

,

mert a P’ pont y koordinátája éppen a P’E’ távolság.

A két egyenletből adódik, hogy

.

Az y vetületi egyenlet tehát:

A pólusokon átmenő vetítősugarak nem döfik a képfelületet, ezért azok – a pólushoz közeli területekkel együtt – a térképen nem ábrázolhatók.

Az x vetületi egyenlet a korábbi okfejtés alapján:

Valamennyi parallelkör képének hossza megegyezik a metszési parallelkörrel, melynek sugara cosj_n , így c= cosj_n . Ha a képfelület érinti a gömböt, akkor az érintési parallelkör – az egyenlítő – lesz hossztartó, és c=cos(0°)=1. (Külső elhelyezésű képfelület esetén c>1, de ezt a kedvezőtlen torzulások miatt a gyakorlatban nem használják.) Vagyis gyakorlatilag:

Mindkét vetületi egyenlet képletében szerepel egy cosj_n tényező, ami a képfelület arányos kicsinyítésével egyenértékű. Tehát egy rögzített f-hez, de különböző hossztartó szélességhez tartozó perspektív hengervetületek egy hasonlósági transzformációval átvihetők egymásba.

A centrális perspektív hengervetületnél a vetítés Q centruma a gömb középpontjába kerül (f=0); az y függvény csak ekkor páratlan, tehát a fokhálózat képe itt szimmetrikus az x tengelyre leképeződő egyenlítőre. Ha viszont f¹0, akkor az egyenlítő képe (j=0) és az x tengely (y=0) nem esik egybe, és a fokhálózat csak az y tengelyre szimmetrikus.

Írjuk fel most a fokhálózat menti torzulásokat.

ahol cosj_n a henger, cosj pedig a parallelkör sugara. A ±j_n metsző parallelkörök tehát hossztartók.

A meridián menti k hossztorzulás minimuma a metsző parallelkörök között van, és 1-nél kisebb. Ettől mindkét pólus felé haladva k értéke nő, és a végtelenhez tart. A h és k torzulások alakulása a j szélesség függvényében (f=0 esetén, a j_n=0° és j_n=30° változatokra) a ???ábrán láthatók. Az érintő vetület egyenlítője torzulásmentes, viszont a metsző (hossztartó) szélességeken a meridián menti hossztorzulások 1-től általában eltérnek, ezért nem torzulásmentesek.

A h és k hossztorzulások nem egyeznek meg, nem is egymás reciprokai, ezért a perspektív hengervetületek általános torzulásúak. A területtorzulási modulus:

mutatja, hogy a pólusok felé haladva a területtorzulások rohamosan nőnek, míg a szögtorzulások növekedése mérsékeltebb. A maximális szögtorzulás f=0 esetén:

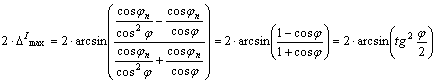
A perspektív hengervetület elsősorban az egyenlítőhöz közeli területek, de semmiképpen sem a magasabb szélességek ábrázolására javasolható.

A transzverzális perspektív hengervetület tulajdonságait a XIX.sz. elején Wetch vizsgálta.

Kvázi-perspektív hengervetületek

Tágabb értelemben perspektív vetületeknek tekinthetjük az olyan leképezéseket, ahol a vetítés középpontja nem egy rögzített pont, hanem a leképezett pont földrajzi hosszúságától függően mozog. Ilyen kvázi-perspektív vetületet kaphatunk pl. úgy, hogy bármely P (j,l) ponthoz a vetítés középpontjának a gömbfelületen a l meridián és az egyenlítő metszéspontjának átellenes pontját, vagyis a (j=0°,l±180° ) pontot választjuk (???ábra). A P’ pont síkkoordinátái:

,

ahol ±j_n a metsző parallelkörök szélessége. A vetületet megalkotójáról Gall féle (sztereografikus) hengervetületnek nevezik. J. Gall brit térképész (1855) a metsző szélességet ±45°-nál vette fel. A vetület általános torzulású. Ezt a vetületet használták az 1937-es kiadású Nagy Szovjet Világatlaszban, a metsző szélességet ±30°-nak választva.

A Gall vetület érintő esetének tekinthető a Braun-féle sztereografikus hengervetület (1867):

Szolovjov orosz kartográfus a Szovjetúnió területének ábrázolására ferdetengelyű kvázi-perspektív vetületet ajánlott (1937).

Nem-perspektív hengervetületek

Az ide tartozó legfontosabb vetülettípusok: a meridiánban hossztartó, a szögtartó és a területtartó valódi hengervetületek.

Ha a vetületi egyenleteik a bevezetőben megadott alakúak (vagyis y=y(j) egy j -ben páratlan függvény, és x =c×arcl+d), akkor normális hengervetületről van szó. Transzverzális ill. ferdetengelyű hengervetületről akkor beszélünk, ha valamilyen (j^*,l^*) segédföldrajzi koordinátarendszerre vonatkozólag a vetületi egyenletek

alakúak, ahol j^* és l^* a (j,l) földrajzi koordinátákból számíthatók gömbháromszögtani úton.

Meridiánban hossztartó valódi hengervetületek

A meridiánok hossztartásából:

vagyis

tehát

Az x vetületi egyenlet megadásához rögzíteni kell, hogy az egyenlítő vagy valamely ±j_n szélességi kör-e a hossztartó. Hossztartó egyenlítő esetén

az utóbbi esetben pedig

A fokhálózat menti torzulások:

Általában , ill. hossztartó egyenlítő esetén .

A meridiánok hossztartása miatt a fentiek szerint

.

A h és k függvények grafikonja a j_n=0° és j_n=30° változatokra a ???ábrán látható. Az elsőnél h az egyenlítőn kívül mindenütt nagyobb k-nál, és az egyenlítő torzulásmentes. A második változatban a hossztartó parallelkör torzulásmentes, és |j|£ j_n esetén h£k, míg |j|³ j_n esetén h³k. A vetület általános torzulású. A területtorzulású modulus:

A maximális szögtorzulás |j|£ j_n esetén:

,

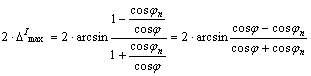míg |j|³ j_n esetén

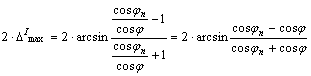
Az egyenlítőben hossztartó változat esetében:

A meridiánban hossztartó valódi hengervetület egyenlítőben hossztartó változatát négyzetes hengervetületnek hívják. Más nyelveken elterjedt a francia eredetű „plate carrée” elnevezés. A fokhálózata ugyanis – a szélességi és hosszúsági körök megegyező sűrűségű ábrázolása esetén – négyzetháló. Már az Ókorban is ismerték, első alkalmazása Eratosthenes nevéhez fűződik. Elsősorban az egyenlítő (transzverzális vagy ferdetengelyű elhelyezés esetén a segédegyenlítőnek kijelölt gömbi főkör) környékének ábrázolásához alkalmas, de használják az egész Föld ábrázolásánál (pl. időzóna térképekhez), vagy csillagtérképek vetületeként.

A meridiánban hossztartó vetület ±j_n szélességi körökben hossztartó változatát Marinus féle vetületnek is hívják a tyrosi Marinusról, aki először készített térképéhez ilyen fokhálózatot a Mediterráneumban felvett hossztartó szélességi körrel. Felhasználása hasonló a négyzetes hengervetületéhez, de a hossztartó parallelkörök helyes megválasztásával az egyenlítő környéki előnyös torzulási övezet kiszélesíthető.

Transzverzális elhelyezésben – feltéve, hogy az egyenlítő képe az x tengely – a vetületi egyenletek

és

alakúak, ahol j_n* a hossztartó segédparallelkör. Jelöljük a segédegyenlítő szerepét játszó középmeridiánt l_K-val. Ekkor a fokhálózat transzformációs egyenletei – figyelembe véve, hogy a segédpólus az egyenlítőre esik:

és

Ezek felhasználásával kapjuk, hogy

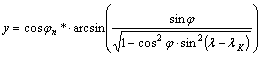
A transzverzális négyzetes hengervetületet (j_n*=0) Cassini vetületnek nevezik (???ábra). Ennek ellipszoid-alapfelületű változata a Cassini-Soldner féle vetület, amelyet a Habsburg Monarchia második katonai felméréséhez használtak. (Ez az ú.n. „vetületnélküli rendszer”.)

Vegyünk egy két meridián által közrezárt, 30°-os nyílásszögű gömbkétszöget (sávot), és ábrázoljuk ezt Cassini vetületben úgy, hogy a sáv középmeridiánja legyen a segédegyenlítő. A felbontást és a vetületi sávokat („zónákat”) mutatja be a ???ábra. A középmeridián és a rá merőleges gömbi főkörök – köztük az egyenlítő – hossztartó módon képeződnek le. A Földet 12 ilyen gömbkétszögre bontjuk és ezekből egyenként zónatérképeket készítünk, amelyeket egy megfelelő méretű gömbre kasírozva, földgömböt kapunk. (A hézagmentes kasírozás érdekében a sávok mindkét szélén a gyakorlatban 1-1°-os átfedést hagynak.) A földgömbkészítésnek ez a hagyományos technológiája csak a legutóbbi évtizedekben szorult háttérbe.

A négyzetes hengervetület ferdetengelyű változatát a ???ábra szemlélteti.

Szögtartó hengervetület

A szögtartás alapegyenlete

,

ami valódi vetületeknél:

alakú. Hengervetületek esetén ebből a

egyenletet kapjuk. Az egyenletet megoldva:

, majd

Az y függvény akkor lesz páratlan, ha a d integrációs konstans 0, tehát

Látható, hogy j=±90° esetén nincsen értelmezve, a pólusvonal képe a végtelenbe távolodik.

Egy algebrai átalakítás eredményeként az y vetületi egyenlet más alakban is felírható:

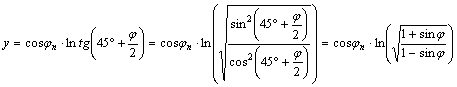
Vagyis

Az x vetületi egyenlet itt is

.

Az egyenlítőben (j_n=0°) és a ±j_n szélességen hossztartó vetületek között mind x, mind y irányban egy cosj_n konstans szorzó adja meg a kapcsolatot, ami egy arányos kicsinyítést („redukálást”) jelent. A különböző szélességeken hossztartó szögtartó hengervetületek ezek szerint – a perspektív vetületekhez hasonlóan – egy hasonlósági transzformációval mindig átvihetők egymásba.

Az alapegyenlet miatt

,

e függvények menete a ???ábrán látható. A hossztartó szélességek torzulásmentesek. A területtorzulási modulus:

.

Ez a vetület elsősorban az egyenlítő környékének szögtartó ábrázolására előnyös, hossztartónak véve keskenyebb övezet esetén az egyenlítőt, szélesebb övezet esetén pedig alkalmasan megválasztott ±j_n szélességet. Az egyenlítőben hossztartó (j_n=0°) változatban j=±60° foknál a hossztorzulás kétszeres, a területtorzulás négyszeres. Innen a pólusok felé haladva e torzulások rohamosan növekednek. A teljes Föld nem ábrázolható, a gyakorlatban a j=±70-75°-on túli területet az ábrázolásból elhagyják.

A szögtartó hengervetület fontos tulajdonsága, hogy a loxodrómák egyenesekre képeződnek le. A meridiánok (a=0°) és a parallelkörök (a=90°) mint speciális loxodrómák képei ugyanis a valódi hengervetületben nyilván egyenesek. Egyéb (0°<a<90°) loxodrómák az alapfelületen minden meridiánt a szög alatt metszenek, ezért a szögtartás miatt e loxodrómák képei is ugyanilyen szög alatt kell messék a meridiánképeket. Az a vonal, amely egy párhuzamos egyenessereg mindegyikét ugyanolyan szög alatt metszi, nem lehet más, csak egyenes, és ezzel az állítást beláttuk.

Az állítás meg is fordítható: a szögtartó hengervetületben a térképi egyenes mindig loxodróma képe. A meridiánokra és parallelkörökre ez nyilvánvaló. Más egyenesek valamilyen a’ (0°<a’<90°) szög alatt metszik a meridiánokat, ami a szögtartás miatt meg kell egyezzen a-val. A térképi egyenes ősképe tehát egy olyan alapfelületi vonal, amely a meridiánokat mind a szög alatt metszi, vagyis loxodróma.

A szögtartó hengervetület egyenlítőben hossztartó változatát először Mercator alkalmazta 1569-ben készült világtérképéhez. Ezt követően a navigációs térképek évszázadokon keresztül ebben a róla elnevezett Mercator vetületben készültek, mert a nyílt tengeri hajózás, majd a távolsági repülés egészen a XX. század közepéig loxodrómák mentén történt. Egy ilyen térképen az indulási és érkezési pontokat egy egyenessel összekötve, majd ezen egyenesnek a meridiánnal bezárt szögét lemérve, megkapható a loxodróma útvonal azimutja, ebből pedig a követendő haladási irány.

A szögtartó hengervetület transzverzális változata a geodéziában és topográfiában játszik szerepet. Ennél a vetületnél a segédegyenlítőnek választott meridián torzulásmentes, ettől mind K-re, mind Ny-ra a torzulások növekednek. Hasonlóan a Cassini vetülethez, a Föld gömbkétszögekre bontható, melyek középmeridiánját segédegyenlítőnek választva, a Föld képe vetületi sávokon („zónákon”) jelenik meg. Az ilyen típusú vetületeket összefoglaló néven transzverzális Mercator vetületeknek nevezik. Ennek vetületi egyenletei (l_K-val jelölve a gömbkétszög középmeridiánját) a Cassini-vetületnél felhasznált fokhálózat-transzformációs képletek felhasználásával:

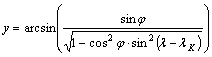
A transzverzális Mercator vetületek közé sorolják a Föld topográfiai térképezéséhez használt Gauss-Krüger vetületet és az UTM (Universe Transverse Mercator grid) vetületet, amelyekben az alapfelület ellipszoid, a zónaszélesség 6°, az előbbinél a középmeridián, az utóbbinál két „segédparallelkör” hossztartó. A geodéziai felmérésekhez többnyire 2 és 3°–os zónaszélességet választanak.

Ugyancsak előfordul a topokartográfiában a szögtartó hengervetület ferdetengelyű változata. Ehhez válasszuk vetületi kezdőpontnak a segédegyenlítő és a l_K középmeridián K metszéspontját (ld. ábra???), melynek szélességét jelölje j_K . A vetületi egyenletek

és

alakúak, a fokhálózat-transzformációt pedig az alábbi egyenletek adják meg:

valamint

vagy

Behelyettesítés után kapjuk a vetületi egyenletekre:

és

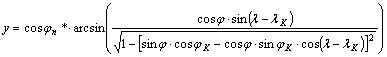
vagy szokásosabban

Az inverz vetületi egyenletek megadásához induljunk ki a vetületi egyenletek átrendezéséből:

Vezessük most be a

és a

jelölést, és az első egyenletből fejezzük ki cos(l–l_K) –t:

Ezt helyettesítsük vissza a második egyenletbe, és abból fejezzük ki sin(l–l_K) –t:

.

Másrészt ez az egyenlőség felírható cos(l–l_K) segítségével a

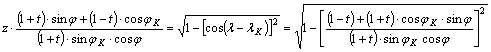
alakban. Négyzetreemelés és közös nevezőre hozás után sinj -ben másodfokú egyenletet kapunk:

Ennek megoldása sinj -re:

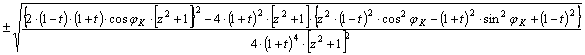
Az egyszerűsítések elvégzése után:

A képletben szereplő második tag a l_K hosszúsághoz mint középmeridiánhoz tartozó félteke azon pontjaira, amelyek a K vetületi kezdőponttól 90°-nál kisebb gömbi távolságra vannak, + előjellel, a félteke többi pontjára – előjellel veendő figyelembe.

Ha sinj már megvan, akkor sin(l–l_K) és cos(l–l_K) a fenti képletekkel kiszámítható. Visszahelyettesítve sinj -t a sin(l–l_K) képletébe kapjuk, hogy

,

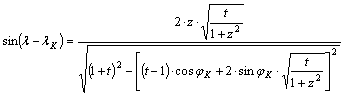amely a (l–l_K) hosszúságkülönbséget a l_K hosszúsághoz mint középmeridiánhoz tartozó félteke azon pontjaira adja meg, amelyek a K vetületi kezdőponttól 90°-nál kisebb gömbi távolságra vannak.

A magyarországi topográfiai térképezés 100 év óta elterjedten használja a ferdetengelyű szögtartó vetületet. A XX. sz. eleje (1908) után vezették be a három ilyen vetületből álló Henger Északi, Henger Középső, Henger Déli rendszert. A kettős vetítés elve alapján a Bessel-ellipszoid alapfelületről először itt is az első magyarországi Gauss-simulógömbre (R=6378512.966m), majd második lépésben a ferde hengerekre képeztek le Mercator vetületével, vagyis cosj_n*=1 választással. Mindhárom hengervetület vetületi kezdőpontja a gellérthegyi meridiánon van, az alábbi gömbi szélességeken:

HÉR: j_K=48° 40’ 2.0”

HKR: j_K=47° 06’ 0.0”

HDR: j_K=45° 31’ 59.0”

Az ezeken a pontokon átmenő harántkörök (segédparallelkörök) torzulásmentesek, innen É és D felé haladva a hossz- és területtorzulások nőnek, és a segédegyenlítőtől mintegy 90 km távolságban érik el az 1.0001 hossztorzulást.

A hetvenes években létrehozott Egységes Országos Térképrendszer (EOTR) vetülete egy ferdetengelyű „redukált” szögtartó hengervetület (Egységes Országos Vetület, EOV), amely a Henger Középső rendszer továbbfejlesztett változatának tekinthető. A leképezés az IUGG’67-es ellipszoidról mint alapfelületről a második magyarországi Gauss-gömbre (R=6379296m), majd innen a cosj_n*=0.99993 tényezővel redukált ferdetengelyű hengerre történik szögtartó hengervetület segítségével. A vetületi kezdőpont a gellérthegyi meridiánon, a j_K=47° 6’ 0.0” gömbi szélességen van. Az EOV-ben két harántkör (segédparallelkör) torzulásmentes, melyek között a hossz- és a területtorzulás 1-nél kisebb, az ezeken kívüli területeken 1-nél nagyobb; az ország területén fellépő legnagyobb hossztorzulás az egységtől csak 10^-4 nagyságrendben tér el.

Területtartó hengervetület

A területtartás alapegyenlete:

,

vagyis

.

Átrendezve:

,

innen kapjuk, hogy

,

és az y akkor lesz páratlan függvény, ha d=0, vagyis

.

Az x vetületi egyenlet a hengervetületekre jellemző

A meridián menti k hossztorzulás:

A h és k függvények menetét a j_n=0° és j_n=30° változatokra a ???ábra mutatja. Látható, hogy a hossztartó egyenlítő ill. a hossztartó szélességi körök torzulásmentes(ek).

A maximális szögtorzulás |j|£ j_n esetén:

,

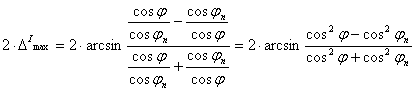míg |j|³ j_n esetén

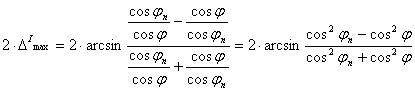
Az egyenlítőben hossztartó változat esetében:

.

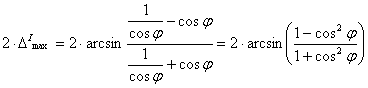A területtartó hengervetület egyenlítőben hossztartó változata Lambert nevéhez fűződik, ezért szokás Lambert féle területtartó hengervetületnek nevezni. Főként az egyenlítő környékének területtartó ábrázolására használják. A teljes Föld ábrázolásához nem ajánlják, a pólusok környékén fellépő nagy szögtorzulások miatt.

Az egyenlítő környéki előnyös torzulási övezet kiszélesíthető, ha alkalmas ±j_n parallelköröket választunk hossztartónak. Behrmann 1910-ben kimutatta, hogy a ±80° között 10°-onként vett maximális szögtorzulások átlaga j_n=±30°-os választásnál a legkisebb. A teljes Föld területtartó ábrázolásához ezért ezt ajánlotta.

Peters 1967-ben egy olyan (erősen vitatott) vetületet javasolt a Föld ábrázolására, amely közelítőleg a j_n=±46°-os szélességeken hossztartó, területtartó hengervetülettel egyezik meg.