EGYÉB KÉPZETES VETÜLETEK
A képzetes henger-, kúp- és síkvetületeken kívül még igen sok képzetes vetületet ismerünk. Közös tulajdonságuk, hogy sem a fokhálózatra, sem a vetületi egyenletekre nézve semmilyen kikötés sincsen. Ebből adódóan lehetnek közöttük mind szögtartók, mind területtartók, mind általános torzulásúak. A torzulási függvények: a fokhálózat menti torzulások, a maximális és minimális hossztorzulások, stb. emiatt csak a bármely vetületre vonatkozó legáltalánosabb képletek alapján számíthatók.
Részletesebben azokkal foglalkozunk, amelyek a gyakorlatban sűrűn kerülnek alkalmazásra. Ezeken túl megemlítünk néhányat, amelyek vagy elméleti szempontból nevezetesek, vagy érdekességként ismertek.
Célunk, hogy az egész Földet egy olyan ellipszis kontúrban jelenítsük meg, amelynek nagytengelye - az egyenlítő képe - kétszer akkora, mint a kistengely - a középmeridián képe, és az egyenlítő meg a középmeridián hossztartó. Arra törekszünk továbbá, hogy a kontinensek kevésbé torzuljanak, mint a korábban tanult, ugyanezen tulajdonságokkal rendelkező Apianus II. képzetes hengervetülete.
Kiindulásul írjuk fel a féltekét körkontúrban ábrázoló transzverzális Postel féle síkvetületet. Ehhez először adjuk meg sinl* és cosl* képletét transzverzális elhelyezés esetén. Az N csúccsal szemközti oldalra felírt gömbháromszögtani oldal-koszinusz tétel szerint (ld. ??? ábra):
![]()
Ugyancsak az oldal-koszinusz tétel átrendezéséből, melyet az N* csúccsal szemközti oldalra írtunk fel:
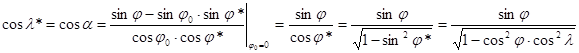
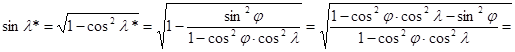
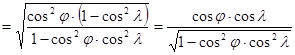
E képletek felhasználásával Postel transzverzális vetületének egyenletei:
![]()
![]()
és hasonlóan
![]()
A határoló meridiánok - a jobb és baloldali kontúrvonalak - l=±90° behelyettesítésekor adódnak.
Hajtsunk most végre egy ![]() -szörös merőleges affinitási
transzformációt az y tengelyre merőlegesen és egy
-szörös merőleges affinitási
transzformációt az y tengelyre merőlegesen és egy ![]() -szöröset az x tengelyre
merőlegesen, ami az x vetületi egyenlet
-szöröset az x tengelyre
merőlegesen, ami az x vetületi egyenlet ![]() -vel, az y vetületi
egyenlet
-vel, az y vetületi
egyenlet ![]() -vel való beszorzásával
valósítható meg. Ennek hatására a félteke a kívánt alakú ellipszisre képeződik
le. Ha ezen az ellipszisen az egész Földet akarjuk ábrázolni, akkor egy
Wagner-transzformációt kell végrehajtanunk m=1 és n=1/2
mellett. Képletben:
-vel való beszorzásával
valósítható meg. Ennek hatására a félteke a kívánt alakú ellipszisre képeződik
le. Ha ezen az ellipszisen az egész Földet akarjuk ábrázolni, akkor egy
Wagner-transzformációt kell végrehajtanunk m=1 és n=1/2
mellett. Képletben:
![]()
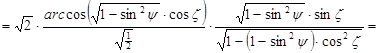
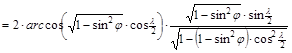 ,
,
végül
![]() ;
;
és
![]()
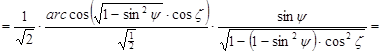
![]() ,
,
tehát
![]()
A vetületi egyenletekből
látható, hogy ![]() és
és ![]() , ezért az egyenlítő és a
középmeridián hossztartó.
, ezért az egyenlítő és a
középmeridián hossztartó.
A torzulásokat az alábbi parciális deriváltakból számíthatjuk:
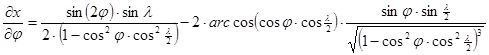
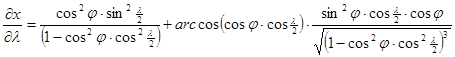
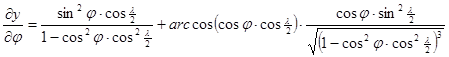
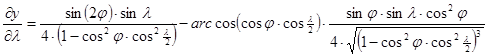
Minthogy Postel vetülete általános torzulású volt, az erre végrehajtott merőleges affinitási transzformációk és a Wagner-transzformáció ezen nem változtatott, így Aitoff vetülete is általános torzulású.
A Föld képe Aitoff vetületében a ??? ábrán látható.
Ez az 1889-ben publikált vetület David Aitoff (!4H@&) orosz kartográfustól származik. Újabban világtérképek vetületeként alkalmazzák. Átszámozott fokhálózatú változatai (ívelt pólusvonallal) kedvező átlagos torzultságuk miatt elterjedőben vannak.
Az Aitoff vetület mintájára hozzunk létre területtartó képzetes vetületet ellipszis-kontúrban. Ehhez induljunk ki a féltekét kör alakban ábrázoló transzverzális Lambert féle síkvetületből, melynek vetületi egyenletei az alábbiak:
![]()
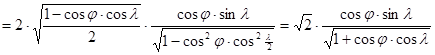
és
![]()
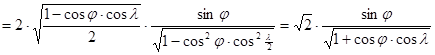
(Itt sinl* és cosl* fenti képletén kívül felhasználtuk, hogy
![]() .)
.)
Ismételjük meg Aitoff
eljárását a transzverzális Lambert féle síkvetületre: hajtsunk végre egy ![]() -szörös merőleges affinitási
transzformációt az y tengelyre merőlegesen és egy
-szörös merőleges affinitási
transzformációt az y tengelyre merőlegesen és egy ![]() -szöröset az x tengelyre
merőlegesen, valamint egy Wagner-transzformációt m=1 és n=1/2
értékekkel. Az eredmények - Hammer vetületének egyenletei - képletben:
-szöröset az x tengelyre
merőlegesen, valamint egy Wagner-transzformációt m=1 és n=1/2
értékekkel. Az eredmények - Hammer vetületének egyenletei - képletben:
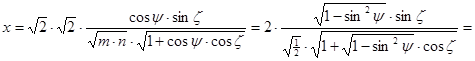
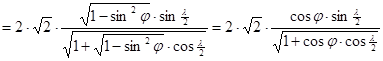
és
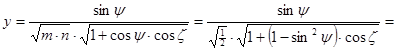
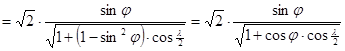
Hammer vetülete az egész Földet ellipszis kontúrban ábrázolja, éspedig – mivel mind a fenti x és y irányú merőleges affinitások együttes hatása, mind a Wagner transzformáció a területtartást megőrzi – a kapott vetület területtartó.
A torzulások részletesebb meghatározásához szükségünk lehet a parciális deriváltakra:
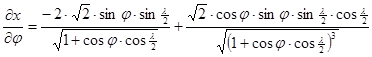
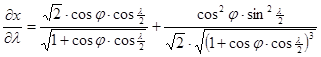
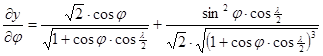
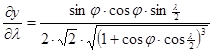
A Föld képe Hammer vetületében a ???. ábrán látható.
??? Hammer német térképész ezt a vetületet 1892-ben publikálta. Területtartó világtérképek vetületeként napjainkban igen kedvelt. Átszámozott változatban (ívelt pólusvonallal) is használják.
Pécsi Albert földrajztudós 1930-ban a Föld legfontosabb termőterületeinek ábrázolására olyan ferdetengelyű Hammer féle vetületet használt, amelynél a vetületi kezdőpont a Greenwich-i meridián 30°-os szélességén helyezkedik el. A segédegyenlítő (és ezzel az előnyös torzulású zóna) beállítása következtében a kedvező adottságú mezőgazdasági területek összességükben kevéssé torzulnak. Pécsi ezt a vetületet a „termelés térképvetületének” nevezte.
A Bartholomew cég atlaszában használt ferdetengelyű Hammer féle vetület vetületi kezdőpontja a 45° É-i szélességre, Ny-Európába kerül („Nordic” vetület). A kontinensek alakjának deformációja itt jóval enyhébb, mint a normális elhelyezés esetén. A Föld képe e vetületben a ??? ábrán látható.
Winkel vetülete
Készítsük el egy meridiánban és a j0 szélességi körön hossztartó valódi hengervetületnek és Aitoff vetületének a keverékét, külön átlagolva az x és az y vetületi egyenleteket. Ekkor
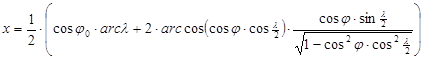
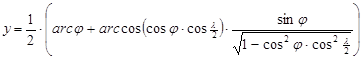
A vetület pólusvonalas; a pólusvonal egyenes, hossza a valódi hengervetület hossztartó parallelköre hosszának a fele. Az egyenlítő ekvidisztáns, hossza a hossztartó egyenlítő és a hossztartó parallelkör hosszának átlaga, tehát itt hosszrövidülés lép fel. A középmeridián hossztartó. A j0 szélességet Winkel 50° 28’-ben adta meg. Később a j0=40° választás terjedt el.
A torzulások kiszámítása az alábbi parciális deriváltakon át lehetséges.
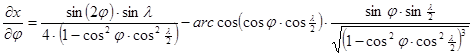
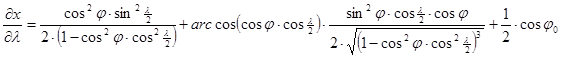
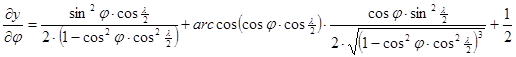
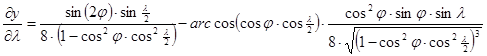
Winkel vetülete általános torzulású. Az átlagos torzultsága a gyakorlatban használt vetületek között a legkisebb, a kontinensek alakjai csak csekély mértékben deformálódnak.
A Föld képe Winkel vetületében (a j0=40°) a ??? ábrán látható.
Oswald Winkel "Tripel"-nek nevezett vetületét 1921-ben hozta nyilvánosságra. Az európai geokartográfia, de kivált a német nyelvterület egyik legkedveltebb vetülete világtérképek számára. Iskolai térképekhez is használják.
A parallelkörök képei ellipszisek, a meridiánok képei hiperbolák. (Az ilyen fokhálózattal rendelkező vetületek összességét "von der Mühl vetületcsaládnak" nevezik.) A parallelköröket ábrázoló ellipszisek és a meridiánokat ábrázoló hiperbolák közös fókuszú görbeseregek, ennél fogva a fokhálózat ortogonális.
A vetületi egyenletek:
![]()
![]()
A félteke képe a teljes sík; a fél egyenlítő a két fókuszpontot összekötő egyenes szakaszra, a ±90°-os határoló meridiánok az ennek folytatásában elhelyezkedő két félegyenesre képeződnek le. A torzulások a parciális deriváltakból következnek:
![]()
![]()
![]()
![]()
Ezekből kiszámítható, hogy ctgq =0 (azaz q =90°), továbbá h=k; következésképpen a vetület szögtartó. A meridiánok a pólusok felé haladva széttartanak, emiatt a területtorzulások a magasabb szélességeken rohamosan nőnek.
A K-i félteke nagy részének képe Littrow vetületében a ??? ábrán látható.
Joseph Johann Littrow osztrák csillagász 1833-ban mutatta be vetületét. Gyakorlati jelentősége csekély, a XX. században a vetületek csoportosításának elméleti kérdései irányították rá a figyelmet.