Képzetes hengervetületek

 

A (segéd-) parallelkörök képei párhuzamos egyenesek, a (segéd-) meridiánok képei tetszőleges törvényszerűséget követő vonalak. A valódi hengervetületekhez hasonlóan a koordinátarendszer y tengelye a középmeridián képe, x tengelye pedig az egyenlítő képe. A (segéd-) fokhálózat általában e két tengelyre szimmetrikus. Az x=x(j,l) vetületi egyenlet tehát l-ban páratlan és szigorúan monoton növő, j-ben páros, míg az y=y(j)  j-ben páratlan és szigorúan monoton növő. A (segéd-) meridiánok és a (segéd-) parallelkörök a tengelyeken kívül általában nem metszik egymást merőlegesen, emiatt a képzetes hengervetületek vagy területtartók, vagy általános torzulásúak, de nincsen közöttük szögtartó.

 

Az y vetületi egyenlet nem függ l-tól, ezért dy/dl=0. A fokhálózat menti torzulások emiatt az általános képleteknél egyszerűbb alakúak:

 

 

 

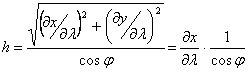
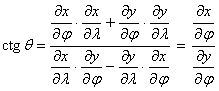                (x/l¹0, ezért egyszerűsíthettünk vele)

 

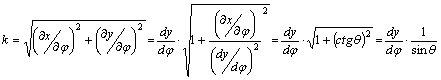
A torzulási ellipszis a és b féltengelye a   összefüggés felhasználásával:

 

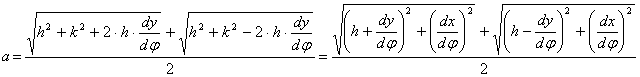
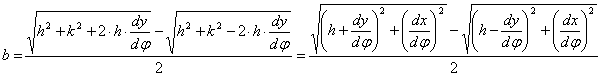
A területtorzulási modulus:      

 

A területtartó (t =1) képzetes hengervetületekre ekkor fennáll a    egyenlet, ahonnan

következik. Vagyis    csak a  j  szélesség függvénye, nem függ a  l  hosszúságtól, tehát az  x=x(j,l)  vetületi egyenlet  l-nak lineáris függvénye. Ebből adódóan a területtartó képzetes hengervetületek parallelkörei mindig ekvidisztánsak (egyenközűek).

 

A  j1, j2  szélességi körök és a  l1, l2  hosszúsági körök által határolt foktrapéz képének területe:

 

A pólusok környékének torzulását lényegesen befolyásolja, hogy a pólus egy pontra, vagy egy - az egyenlítő képével párhuzamos – egyenesre képeződik-e le: az esztétikailag tetszetősebb póluspont közelében a torzulások általában igen nagyok.

 

A képzetes hengervetületeket elsődlegesen a meridiánívek jellege alapján osztályozzuk. A legfontosabbak a  szinuszíves és az ellipszisíves vetületek, de más meridiánívek is előfordulnak. A további osztályozási szempontok alapján a képzetes hengervetületek lehetnek tehát póluspontosak vagy pólusvonalasak, és területtartók vagy általános torzulásúak.

 

 

Szinuszíves képzetes hengervetületek

 

 

Mercator-Sanson (másnéven Sanson-Flamsteed) féle vetület

 

Írjunk elő egy képzetes hengervetületben hossztartást a szélességi körök és a középmeridián mentén, vagyis legyen h=1 és k(l=0°)=1. E feltételekből következik (figyelembe véve a fokhálózat szimmetriáit):

 ,  vagyis

 ,  vagyis

Helyettesítsük vissza az x vetületi egyenletbe j helyére y-t. Ha most változatlan l mellett y végigfutja a –p/2 és p/2 közötti értékeket, az x(y) függvény grafikonja egy félperiódusnyi koszinusz-ív affin képét írja le. Az ilyen görbéket nevezik “szinuszívnek”, a továbbiakban mi is ezt az elnevezést használjuk.

 

A fokhálózat menti torzulások:

 , 

tehát a vetület a felsorolt tulajdonságok mellett területtartó. Végül

Innen a k közvetlenül felírható j és l függvényében:

 

A ???. ábra mutatja a különböző l hosszúságokhoz tartozó k és q értékek grafikonjait. Ezek szerint az egyenlítő környékén a torzulási viszonyok igen kedvezőek, viszont magas szélességeken a határoló meridiánok környékén igen nagy meridián menti hossztorzulások és szögtorzulások léphetnek fel. Ezt támasztja alá a maximális szögtorzulás értéke is, amely az

  és    egyenlőségek alapján:

 

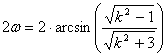
A ±180°-os határoló meridiánnál ez 60°-os szélességen 107.36°, 75°-on 113.22° . Ugyanitt a meridián menti hossztorzulás: k60°=2.90, k75°=3.20. A pólus környékén a meridiánok képei úgy összesűrűsödnek, hogy gyakran ritkítva ábrázolják őket.

 

A torzulások alakulása miatt elsősorban egyenlítő környéki kontinentális kiterjedésű területek (Afrika, Dél-Amerika) ábrázolására használják; XIX.-XX. századi világtérképeknél nemigen találkozunk vele. Előfordul kombinációja más vetületekkel (Goode vetületénél pl. a Mollweide félével) .

 

Mercator szerkesztette meg 1606-ban; később Sanson alkalmazta. Flamsteed csillagászati atlaszban használta. Innen ered a “Mercator-Sanson”, illetve az angolszász szakirodalomban a “Sanson-Flamsteed” elnevezés. Szokás még szinuszoidális vetületnek is nevezni.

 

 

Vetületek fokhálózat-átszámozási transzformációja

 

Egy ismert vetületből új vetületet kaphatunk, ha a szélességi és hosszúsági köreit “átszámozzuk”, azaz a j szélességi körnek y átszámozott szélességet, a l hosszúsági körnek z átszámozott hosszúságot tulajdonítunk. Az eredeti x(j,l) és y(j,l)vetületi egyenletekben tehát a j-t  y-vel, a l-t z-val helyettesítjük. Ha az átszámozást a y(j) és a z(l) függvények szerint végeztük el, akkor az  x(y(j),z(l))  és  y(y(j),z(l))  a  j,l  földrajzi koordinátájú ponthoz más képpontot rendel hozzá, mint az eredeti  x  és  y  vetületi egyenletek.

 

A y(j) és a z(l) átszámozási függvények szélességhez szélességet, hosszúsághoz hosszúságot rendelnek, ennél fogva az eredeti vetület szélességi körei az átszámozás után is szélességi körök, az eredeti hosszúsági körök az átszámozás után is hosszúsági körök maradnak. Maga az átszámozás végső soron a fokhálózat transzformációjának tekinthető, mely független az alkalmazott vetülettől.

 

A fokhálózat-átszámozási transzformáció – általában a kiindulási vetület méretviszonyainak helyreállítása céljából – tartalmazhat még egy-egy merőleges affinitást a síkkoordináta-tengelyek irányában. Az eredeti x(j,l) és y(j,l) vetületi egyenletek által meghatározott vetület átszámozási transzformáltjának vetületi egyenletei tehát általában c×x(y(j),z(l))  és  d×y(y(j),z(l))  alakúak. A y(j) és z(l) átszámozási függvényeknek természetesen eleget kell tenniük a szigorúan monoton növekedés és a folytonos differenciálhatóság feltételének. Világtérképeknél célszerű továbbá az egyenlítő szélességét az átszámozás során változatlanul hagyni. A ???. ábra szemlélteti, hogy az eredeti vetületből az átszámozási transzformáció eredményeként hogyan keletkezik új vetület.

 

A vetületek átszámozási transzformációja a fentiek szerint a szélességi és hosszúsági körök képeinek jellegét (vagyis az ívek típusát) nem változtatja meg. A képzetes hengervetületek transzformáltjai tehát ismét képzetes hengervetületek lesznek, és a meridiánívek is legfeljebb egy merőleges affinitást szenvednek el. Ez a transzformáció tehát nem vezet ki a fokhálózati vonalak jellege alapján kialakított vetületcsoportból.

 

A vetületek átszámozása a gyakorlatban rendszerint úgy történik, hogy egy térkép fokhálózatának belsejéből egy – többnyire kedvező torzulású - részt kiemelünk, és azon egy nagyobb területet, pl. a teljes Földet ábrázoljuk. A transzformáció célja az, hogy az eredeti vetület erősen torzult részei az ábrázolásból kiküszöbölődjenek. Ennek eredményeként a torzulások a térképen egyenletesebben oszlanak el.

 

 

A Wagner-transzformáció

 

A Wagner-transzformáció olyan speciális fokhálózat-átszámozási transzformáció, amelyet alkalmazva egy vetületre, annak területtorzulásai nem változnak, tehát az eredeti vetület területtartása  az új vetületben is megmarad. A transzformáció során változatlanul kívánjuk hagyni a parallelkörök ekvidisztanciáját is. Ez utóbbi feltétel a

 

összefüggést alkalmazva – állandó n esetén – nyilvánvalóan teljesül.

 

A területtorzulás (és a területtartás) megmaradásának feltételéhez tekintsünk az átszámozás előtti,  j,l  földrajzi koordinátákkal jellemzett alapfelületen egy Dl széles, az egyenlítő és valamely  j  ill. jH paralelkör által határolt F foktrapézt, melynek az átszámozás utáni,  y,z  földrajzi koordinátákkal jellemzett alapfelületen egy Dz  széles, az egyenlítő és valamely yH ill.  yH  parallelkör által határolt F’ foktrapéz fog megfelelni (???. ábra). A területtorzulások változatlansága azt jelenti, hogy az eredeti F foktrapéz kisebb foktrapézokra való felosztása az F’ foktrapézon felszínarányos foktrapézokra való felosztást eredményez. Az ábra jelölésével ez az arányosság így írható fel:

 

             , 

ahonnan egyszerűsítés után

 , 

vagyis - figyelembe véve, hogy az

 

mennyiség konstans: 

.

 (Többnyire jH=90°, hogy az egyenlítő és a yH közötti zónára az összes nem-negatív földrajzi szélesség leképeződjön, tehát yH £ jH; ilyenkor nyilvánvalóan m£1.)

 

Hátra van még az átszámozásba beiktatandó két merőleges affinitás  c  és  d  paramétereinek meghatározása. Képezzük le a síkra egy tetszőleges területtartó vetülettel a  j  szélességi kör által határolt Fj  foktrapézt, majd az átszámozás utáni vetülettel a y szélességi kör által határolt Fy  foktrapézt (A foktrapézok felszínét jelöljük m(Fj)-vel és m(Fy)-vel). Ekkor a foktrapézok Tj  és Ty  képének területei a síkon (m(Tj)-vel és m(Ty)-vel jelölve):

Elvégezve itt a behelyettesítést  y-be és  z-ba:

           

A  Tj  és  Ty  idomok területei a fenti egyenlőség miatt csak akkor egyezhetnek meg, ha az átszámozás  c  és  d  arányossági tényezőire teljesül

.

Wagner ezt az “eredeti méretarány visszaállításának” nevezte, és a két merőleges affinitást egy közös

 

arányú hasonlósági transzformációban egyesítette.

 

Ha  m<1,  akkor a  y  által befutott (általában szimmetrikus) szélesség-intervallum kisebb a  j  által befutott eredeti szélesség-intervallumnál. Amennyiben ilyenkor az eredeti vetületünk póluspontos volt, akkor a Wagner-transzformáció utáni vetület pólusa az egyik eredeti parallelkör képére esik, vagyis pólusvonalas lesz.

 

A vetületek átszámozási transzformációjának kidolgozását a XX. század 30-as éveiben két német kartográfus, K. Siemon és K. H. Wagner végezte el.

 

 

A Mercator-Sanson-sor és Kavrajszkij I. vetülete

 

Alkalmazzuk a Wagner-transzformációt a Mercator-Sanson vetületre: -

Wagner ezt a kétparaméteres szinuszíves (és rendszerint pólusvonalas) vetületsokaságot „Mercator-Sanson-sornak” nevezte el. Minthogy a kiindulási vetület területtartási tulajdonságát a Wagner-transzformáció megőrzi, a vetületsokaság tagjai területtartók, parallelköreik tehát ekvidisztánsak, viszont a középmeridiánjuk – ellentétben a kiindulási vetülettel – nem ekvidisztáns.

 

A Mercator-Sanson-sor tagjait jellemezhetjük a térképi fokhálózat főbb méreteinek viszonyával. Jelöljük p-vel a kezdőmeridián és az egyenlítő hosszának arányát, q-val pedig a pólusvonal és az egyenlítő hosszának arányát.

 

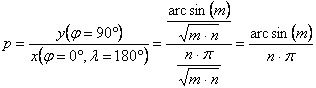
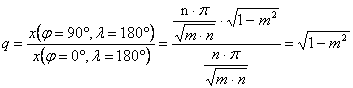
Ezekből az egyenletekből p és q ismeretében m és n meghatározható:

  és 

 

Tekintsük a Mercator-Sanson-sor azon tagját, melynél az egyenlítő térképi hossza kétszer akkora, mint a középmeridián és a pólusvonal hossza, azaz    és   . Ennél a választásnál    és  ,  vagyis 

A vetületi egyenletek tehát:

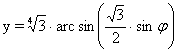
A vetületi torzulások:

 

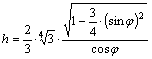
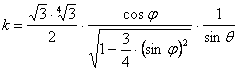
Ez a Kavrajszkij I. vetületének nevezett leképezés tehát valóban területtartó, a parallelkörök ekvidisztánsak, az egyenlítő mentén a hossztorzulás: h=0.8774. A középmeridián nem ekvidisztáns, éspedig az osztásközök az egyenlítő felől a pólusok felé rövidülnek.

 

Ezt a vetületet Kavrajszkij alkotta meg 1936-ban; Wagner 1949-ben megjelent könyvében adta meg a fenti származtatást és besorolást. Az egykori Szovjetunió és a szocialista országok, illetve Oroszország geokartográfiájában világtérképek vetületeként gyakran találkozhatunk vele.

 

 

Keverékvetület létrehozása

 

Két ismert vetületből újat képezhetünk a vetületi egyenleteik átlagolásával. Az ilyen módon létrejött keverékvetület rendelkezhet az eredeti vetületek bizonyos tulajdonságaival. Így pl. képzetes hengervetületek keveréke is képzetes hengervetület lesz; póluspontos vetületek keveréke póluspontos marad, míg az egyenlítőben és középmeridiánban hossztartó vetületek e tulajdonsága szintén átörökítődik. A torzulások a “keverés” során általában kiegyenlítődnek, amitől a kiugróan erős torzulású területek megfogyatkozását várhatjuk.

 

 

Eckert V. vetülete

 

Állítsuk elő a Mercator-Sanson féle vetület és a négyzetes hengervetület keverékét, majd a területtorzulások csökkentése érdekében hajtsunk végre egy c-szeres arányos kicsinyítést, amelynek eredményeként a teljes Földet a keverékvetület egy ugyanakkora területű idomra képezi le.

 

A vetületi egyenletek ez alapján:

 

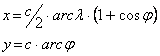
A származtatásból következik, hogy a pólusvonal hossza, amely megegyezik a középmeridián képének hosszával, a térképi egyenlítő hosszának fele. A ??? ábra alapján a fokhálózat egy c·p oldalú négyzetre és két olyan idomra bontható, amelyeket az egyik oldalról egyenes, a másikról görbeív határol; ezek a  függvény görbéje alatti tartomány c-szeres kicsinyítésének foghatók fel. A függvénygörbe alatti terület:

 

 

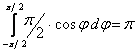
A három idom területe összegének kell tehát a gömb felszínével megegyeznie:

 

,        ahonnan         

A vetületi egyenletek tehát:

 

A fokhálózat menti torzulások:

 

 

 

 

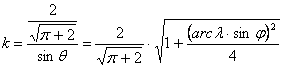
A vetület tehát általános torzulású. A középmeridián és a parallelkörök ekvidisztánsak.

 

Eckert ezt a vetületét 1906-ban publikálta. Alkalmazása főként a német nyelvterület világtérképein, atlaszaiban a mai napig előfordul.

 

 

Módosított földrajzi szélesség bevezetése (a szélességek átszámozása)

 

Tekintsünk egy általános torzulású, középmeridiánban hossztartó, parallelkörökben ekvidisztáns képzetes hengervetületet. A szélességek átszámozásával ("módosított földrajzi szélesség" bevezetésével) ezt területtartó vetületté akarjuk átalakítani úgy, hogy eközben az egyenlítő, a meridiánok és a kontúrvonalak (a határoló meridiánok valamint az esetleges pólusvonal) változatlanul maradnak, viszont megváltozik a parallelköröknek az egyenlítőtől vett térképi távolsága, és ezzel együtt elvész a középmeridián menti hossztartás, sőt az egyenközűség is. Ha ez a vetület az egész Földfelületet egy vele megegyező területű síkidomra képezi le, akkor célunk nyilván megvalósítható; ellenkező esetben az  y=arcj  és  x=x(j,l)  egyenleteket egy alkalmasan megválasztott  c  arányossági tényezővel beszorozva hozzuk létre az egész Föld képére vonatkozó területegyenlőséget.

 

Alkalmazzuk erre a vetületre a  y(j)  szélesség-átszámozást  ( c×arcy  és  c×x(y,l) )  úgy, hogy minden - az ellipszis és a  j  szélességi kör által határolt - gömböv  F= 2×p×sinj  felszíne legyen egyenlő a megfelelő térképi idom  T  területével (ld. ??? ábra). Képletben ez az alábbiakat jelenti:

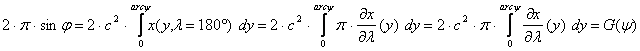
Kaptunk tehát egy    alakú összefüggést, amely egy  y(j)  szélesség-átszámozási függvényt értelmez, ha minden szóba jöhető jöhető  j  értékhez egyértelműen rendel hozzá egy  y  értéket. (A  y  azonban a  G(y)  függvényből nem mindig fejezhető ki, ilyenkor a  y(j)  függvény csak implicit alakban létezik.)  A  y(j)  függvény szigorú monotonitásához  dy/dj>0  szükséges; továbbá a  y(j)  függvénynek  j=0 esetén y=0, j=-90° esetén y=-90°, végül j=90° esetén y=90° értéket kell felvennie, hogy az egyenlítő és a pólusok helyzete ne változzon meg.

 

Az átszámozott  c×arcy  és  c×x(y,l)  egyenletekkel meghatározott vetület már területtartó, mert (felhasználva az implicit függvény deriválására vonatkozó formulát):

=

 .

(Itt felhasználtuk, hogy a  y(j)  implicit függvény  dy/dj  deriváltja a 

  egyenlettel számítható ki.)

 

(Ha a parallelkörökben ekvidisztáns képzetes hengervetületben a középmeridián nem hossztartó, akkor először vezessük be a  z=z ( j)  módosított szélességet a 

képlet segítségével. Az  átszámozott y=y(z)  a  z-ra nézve hossztartó;  most már alkalmazhatunk egy újabb,  y(z)  átszámozást y=y(z) -ra a fenti  y(j)  átszámozás mintájára. A két egymás utáni átszámozás és az esetleges c-szeres hasonlósági transzformáció együttes alkalmazásával tehát területtartó vetülethez jutunk.)

 

Eckert VI. vetülete

 

Ellipszisíves, pólusvonalas területtartó vetület létrehozása érdekében számozzuk át Eckert V. vetületén a  j  szélességi köröket úgy, hogy bevezetjük a  y  módosított szélességet. A vetületi egyenletek eszerint:

 

A  j  és  y  változók közötti összefüggést az egyenlítő és a j szélességi kör közötti  F  felszínű gömbövek területegyenlő leképezése adja meg:

 

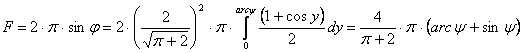
Egyenletünk tehát az alábbi alakot ölti:

Egyszerűen ellenőrizhető, hogy  j=0 esetén y=0, j=-90° esetén y=-90°, végül j=90° esetén y=90°  teljesül. Továbbá

 

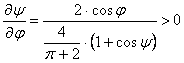 ,  ha  –90° < j, y < 90°

A fenti egyenlet által meghatározott  y(j)  implicit függvény tehát szigorúan monoton növő leképezést létesít, viszont explicit alakban nem adható meg, mert  y  az egyenletből nem fejezhető ki. Emiatt egy adott j szélességhez előbb közelítéssel meg kell határozni a y módosított szélességet, ami egy nem-lineáris egyenlet megoldását igényli; ez után tudunk csak a vetületi egyenletekbe behelyettesíteni.

 

A torzulások:

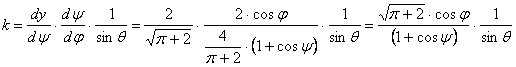
Ezekből számítjuk a területtorzulási modulust:

A vetület tehát valóban területtartó. Végül

Eckert VI. vetülete szintén 1906-ban vált ismertté. Az európai geokartográfiában világtérképekhez elterjedten használják.

 

Felmerül a kérdés, hogy Eckert szinuszíves, pólusvonalas, területtartó VI. vetülete nem tagja-e a Mercator-Sanson-sornak. Minthogy a pólusvonal és a középmeridián hossza éppen úgy fele az egyenlítőének, mint Kavrajszkij I. vetületénél, ezért   és    behelyettesítése után a vetületi egyenleteiknek is meg kellene egyezniük, ami szemmelláthatóan nem teljesül.

 

A két vetület a fokhálózat tekintetében első ránézésre kevés különbséget mutat. Kavrajszkij I. vetületében a fokhálózat méretei mintegy 0.5 %-kal kisebbek; a meridiánívek – szemben Eckert VI. vetületével - nem terjednek ki a teljes (félperiódusnyi) szinuszívekre, hanem csak azok középső 2/3-nyi részére; emiatt a meridiánok görbülete egyenletesebb, és az egyenlítőnél enyhébb.

 

 

Ellipszisíves képzetes hengervetületek

 

Apianus II. vetülete

 

A vetület egyenlítőben és középmeridiánban hossztartó, a félgömböt körkontúrba képezi le, és parallelkörei ekvidisztánsak. E tulajdonságokból következik, hogy meridiánjai a határoló meridián affin képei, vagyis olyan ellipszisívek, amelyek közös tengelye a középmeridián, a másik tengely pedig az egyenlítő megfelelő hosszúságú középső darabjával esik egybe. A ±l hosszúságú meridián képének egyenlete tehát:

,  ahonnan   .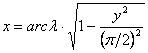

 

  miatt akkor 

E képletek |l|>90° esetén is érvényesnek tekinthetők, ezek alapján tehát e térkép a félgömbön túl is folytatható. A kontúr a teljes gömb ábrázolása esetén ellipszis lesz, az egyenlítővel mint nagytengellyel.

 

Jelöljük most a (köralakú) 90°-os meridián j szélességű pontjához tartozó rádiuszvektor egyenlítővel bezárt szögét c-vel. A ???. ábráról leolvasható, hogy

.

Ennek felhasználásával a vetületi egyenletek az alábbi alakban is felírhatók:

 

Ezek a vetületi egyenletek a teljes gömbre is kiterjeszthetők; ebben az esetben a kontúrmeridián olyan ellipszis, melynek nagytengelye az egyenlítő, feleakkora kistengelye pedig a középmeridián.

 

A fokhálózat menti torzulásokat az eredeti vetületi egyenletből számítjuk:

 

 ,  ahol

 

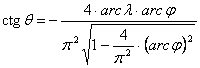
Ezekből a képletekből látható, hogy a vetület, amely Mercator kortársától, Apianus (Peter Bienewitz) szász kartográfustól ered, általános torzulású. A XX. század geokartográfiájában önálló vetületként ritkán használják, de több más fontos (Eckert féle III., Mollweide féle) vetület származtatásánál játszik szerepet.

 

 

Mollweide vetülete

 

Apianus teljes Földre kiterjesztett II. vetületéből - módosított szélességek bevezetésével - területtartó vetületet akarunk készíteni. Ehhez először is egy c-szeres hasonlósági transzformáció közbeiktatása során a teljes Föld képének területét a gömbfelszínnel tesszük egyenlővé. A kontúrmeridián által határolt ellipszis T területe:

 .

Ennek kell megegyeznie a gömb F felszínével, vagyis:

 ,  ahonnan   =0.900316… 

 

Vezessük most be a  y  átszámozott földrajzi szélességet, amelyet az átalakított vetületi egyenletbe  c  helyére helyettesítünk:

 

Ezek tehát a Mollweide féle vetület egyenletei. A  y(j)  függvényt megadó összefüggés az egyenlítő által határolt gömbövek területegyenlő leképezéséből adódik:

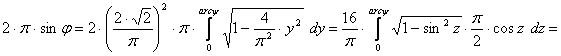
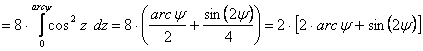
(Itt felhasználtuk, hogy a ???. ábra alapján a térképi idom területe egy ellipszis integráljának kétszerese, majd az integrálban elvégeztük az    helyettesítést továbbá felhasználtuk, hogy  +const.)

 

Egyszerűsítés után:

 

Ebből az egyenletből a  y  nem fejezhető ki. Könnyen ellenőrizhetjük, hogy  j=0 esetén y=0, j=-90° esetén y=-90°, végül j=90° esetén y=90°  teljesül. Ezenkívül

 ,  ha  –90° < j, y < 90°

A fenti egyenletből adódó  y(j)  implicit függvény tehát szigorúan monoton növő. Az adott j szélességhez tartozó y  módosított szélességet közelítő számítással határozhatjuk meg.

 

A vetületi egyenletből következnek a fokhálózat menti torzulások:

Az egyenlítő mentén h=0.900, ettől távolodva h értéke növekszik, j=±40.7367° szélességen h=1, vagyis ez a szélességi kör hossztartó.

A vetület valóban területtartó, mert

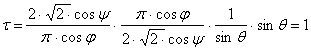
Végül

 

Mollweide német matematikus 1805-ben publikálta vetületét, amely Babinet francia matematikus ajánlása (1857) után népszerűvé vált. Elterjedten használták és használják világtérképekhez, mind atlaszokban, mind falitérképeken. Az oktatási térképek területéről az utóbbi időben kiszorulóban van, a kontinensek elcsavarodását eredményező erős szögtorzulások miatt.

 

Összehasonlítva a szögtorzulásokat a Mercator-Sanson vetület szögtorzulásaival, megállapítható, hogy a fokhálózat által bezárt szögek az egyenlítő és a 65.5° között kevésbé torzulnak a Mollweide féle vetületben; a maximális szögtorzulás értéke 5° és 75° között szintén kisebb, mint a Mercator-Sanson vetületben. Ezért a Mollweide vetületet kombinálják a Mercator-Sanson vetülettel (Goode-féle vetület), valamint a Mercator-Sanson-sorhoz tartozó egyik vetülettel (Érdi-Krausz-féle vetület).

 

A Bartholomew cég atlaszaiban előfordul a transzverzális Mollweide-vetület egy sajátos transzformációja, melynél a segédhosszúságokat 45°-kal megnövelik (természetesen ha a megnövelt segédhosszúság 180°-nál nagyobbnak adódik, akkor ezt követően még 360°-ot levonnak belőle) (ld. ??? ábra).

 

Wagner a Mollweide féle vetületre is alkalmazta transzformációját; a kapott ellipszisíves vetületsokaságot Mollweide-sornak nevezte el, amely a számításigényesség miatt a kartográfiában kevéssé terjedt el.

 

 

Eckert III. vetülete

 

Készítsünk keverékvetületet Apianus II. vetületéből és a négyzetes hengervetületből Eckert V. vetületének mintájára, majd a területtorzulások csökkentése érdekében itt is hajtsunk végre egy c-szeres arányos kicsinyítést a teljes Föld képének területegyenlő leképezése céljából.

 

A vetületi egyenletek ebből:

ahol   ,  Apianus II. vetületének mintájára.

 

A pólusvonal hossza itt is megegyezik a középmeridián képének hosszával, és fele a térképi egyenlítő hosszának. A ??? ábra alapján a fokhálózat képe egy c·p oldalú négyzetre és két   sugarú félkörre bontható. Ennek területe egyezzen meg a gömb felszínével, vagyis:

innen 

 

A vetületi egyenletek tehát:

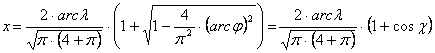
A fokhálózat menti torzulások:

 

A vetület ezek alapján általános torzulású. A középmeridián és a parallelkörök ekvidisztánsak.

 

Eckert 1906-ból származó III. vetülete elsősorban az európai geokartográfiában, világtérképekhez használatos.

 

 

Eckert IV. vetülete

 

Számozzuk át Eckert III. vetületének  j  szélességeit abból a célból, hogy új, területtartó vetülethez jussunk. A  y  módosított szélességet a  c  független változót használó, egyszerűbb alakú vetületi egyenletekbe helyettesítjük, nem feledve eközben, hogy a  c  változó a  j  szélesség függvénye:

 

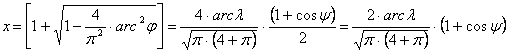
A  y  és  j   változó közötti összefüggést ismét az egyenlítő és a j szélességi kör közötti gömbövek területegyenlő leképezése adja meg:

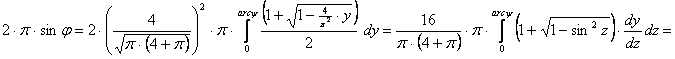
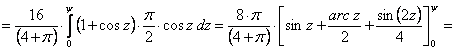
(A Mollweide féle vetülethez hasonlóan itt is végrehajtottunk egy    helyettesítést, továbbá felhasználtuk, hogy  +const  .)

 

Az egyszerűsítések elvégzése után kapjuk az alábbi összefüggést  y  és  j   változók között:

 

 

Ebből az egyenletből  y   nem fejezhető ki. Könnyen látható viszont, hogy  j=0  esetén  y=0,  j=-90°  esetén  y=-90°, végül  j=90° esetén  y=90°  teljesül; továbbá

 

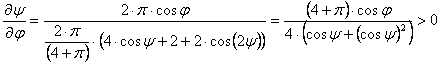 ,  ha  –90° < j, y < 90°

 

A fenti egyenlet által meghatározott  y(j)  implicit függvény tehát létezik. Emiatt egy adott j szélességhez a  y  módosított szélesség csak közelítő számítással (nem-lineáris egyenlet megoldásával) határozható meg.

 

A torzulások:

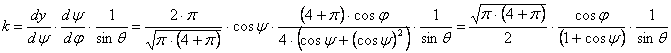
A területtorzulási modulus:

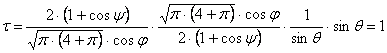
A vetület tehát valóban területtartó. Végül

Eckert IV. vetülete is 1906-ból származik. Világtérképek vetületeként gyakran előfordul.

 

 

Kavrajszkij II. vetülete

 

Kavrajszkijnak ez a vetülete is pólusvonalas; a kezdőmeridián hossztartó, parallelkörei ekvidisztánsak. A vetületi egyenletei:

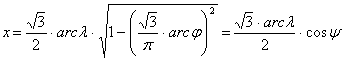
ahol a  y  segédváltozót a

  egyenlet szolgáltatja.

 

Képezzük a 120°-os meridián mentén a  y-t használó vetületi egyenletek segítségével az    mennyiséget:

Ez egy kör egyenlete, vagyis a  ±120°-os meridiánt egy-egy körív alkotja. A parallelkörök ekvidisztanciája miatt a meridiánok merőleges affinitással egymásból előállíthatók, tehát a meridiánívek a 120°-os meridián affin képei, vagyis ellipszisívek.

 

A fokhálózatmenti torzulások:

 

A vetület tehát általános torzulású. Továbbá

 

Kavrajszkij II. vetülete az orosz geokartográfiában igen kedvelt világtérképek vetületeként.

 

 

Köríves képzetes hengervetületek

 

Apianus I. vetülete

 

Ez a vetület póluspontos, egyenlítőben és középmeridiánban hossztartó, ami a szélességi és hosszúsági körök képének helyzetét egyértelműen meghatározza. A félgömb tehát körkontúrba jelenik meg.

 

Az x vetületi egyenlet meghatározásához először határozzuk meg a l hosszúságú meridián képének középpontját. Jelöljük r-val a körív sugarát és x-vel pólushoz vezető rádiuszvektornak az egyenlítővel bezárt szögét. Az  ???. ábráról leolvasható, hogy

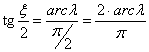
(itt felhasználtuk, hogy azonos körívhez tartozó kerületi szög fele a középponti szögnek). A körív középpontjából felező merőlegest bocsátunk a meridiánív egyenlítői pontját a pólusponttal összekötő szakaszra. Az így keletkezett derékszögű háromszög átfogójából kapjuk a  r  sugarat:

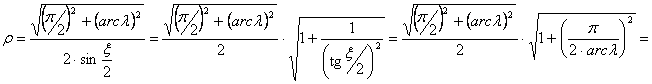
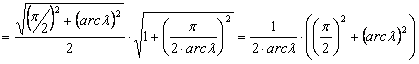
Pozitív hosszúság esetén a körív középpontja az egyenlítő képén az origótól balra    távolságra helyezkedik el. Most már fel tudjuk írni a vetületi egyenleteket:

 

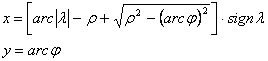
A torzulásokhoz szükség van dr/dl kiszámítására:

 

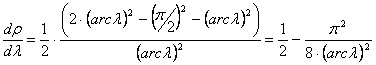
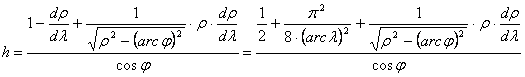
vagyis a parallelkörök nem ekvidisztánsak.

 

A vetület tehát általános torzulású. Apianus 1524-ben tette közzé.

 

 

Ortelius vetülete

 

Apianus I. vetülete a félgömbön egyértelműen van értelmezve, de a teljes gömbre való kiterjesztése többféleképpen is lehetséges. Ennek egyik változata Ortelius vetülete, amely a középmeridiánra szimmetrikus félgömbön megegyezik Apianus I. vetületével; a ±90°-os hosszúsági körökön túli meridiánok képei félkörívek, amelyek helyzetét az egyenlítő hossztartása jelöli ki. A vetületi egyenletek tehát ½l½£90° esetén megegyeznek Apianus I. vetületével. ½l½>90° esetén:

A vetület általános torzulású.

 

Míg Apianus I. vetülete egy félgömbre póluspontos volt, addig Ortelius vetülete pólusvonalas, azzal a többi pólusvonalas vetületeknél szokatlan tulajdonsággal, hogy a meridiánok fele egy póluspontba fut össze. A pólusvonal hossza fele az egyenlítő hosszának.

 

Ez a vetület Battista Agnese XVI. sz.-i kartográfustól származik, a nevét a flandriai Abraham Orteliusrol kapta egy 1570-ből származó térkép alapján.

 

 

Összetett képzetes hengervetületek

 

A vetülettől általában elvárjuk, hogy az ábrázolandó terület egészére érvényes vetületi egyenletekkel rendelkezzen. Mégis időnként - többnyire a kedvezőbb torzulási tulajdonságok érdekében - megengedhető, hogy foktrapézonként változó vetületi egyenlettel adjuk meg a leképezést. Természetesen a kezelhetőség miatt ajánlatos, hogy e foktrapézok száma kettő-háromnál több lehetőleg ne legyen, és a határon - a torzulások folytonos változása céljából - a vetületi egyenletek folytonos differenciálhatóságát általában kikötjük.

 

Összetett vetületek készítése rendszerint úgy történik, hogy a Földet parallelkörök által határolt övezetekre bontjuk, és ezeket övezetenként eltérő vetületben ábrázoljuk. Minden övezetben olyan vetületet használunk, amelynek a torzulása ott az ábrázolás szempontjából előnyös. Leggyakrabban ezért három övezetből tevődik össze az ilyen térkép: az egyik ábrázolja az alacsonyabb és közepes szélességű területeket (az egyenlítőre szimmetrikusan), a két másik pedig a sarkok tágabb környékét.

 

 

Goode féle vetület

 

Ismeretes, hogy a teljes Föld területtartó ábrázolásakor az egyenlítő környékét Mercator-Sanson féle vetületben, míg a pólusok környékét Mollweide féle vetületben tudjuk kedvezőbb torzulásokkal bemutatni. Tudjuk továbbá, hogy míg a Mercator-Sanson féle vetület minden parallelkör mentén hossztartó, addig ez a Mollweide féle vetületnél csak a j=±40.7367° szélességnél igaz, ami a y=32.6893° módosított szélességnek felel meg. Ha tehát felosztjuk a Földet e szélességeknél három övezetre, és minden övezetet az ott előnyösebb vetületben ábrázoljuk, akkor a határoló szélességi köröknél a kétféle vetület éppen összeillik. A vetületi egyenletek –40.7367°£j£+40.7367° között ugyanazok, mint a Mercator-Sanson féle vetület egyenletei:    és  . Ezen a gömbövön kívül az x vetületi egyenlet a Mollweide féle vetületével egyezik meg:

,  ahol ;  továbbá

j>40.7367° esetén   ,   míg

 

j<-40.7367° esetén   .

 

Az egyes övezeteket határoló szélességeknél a meridiánok, amelyek tehát egy szinuszívhez kétoldalt csatlakozó ellipszisívekből állnak, folytonosak ugyan, de megtörnek. Ez itt a torzulások ugrásszerű változását eredményezi, ami nem csak esztétikailag, hanem elvileg is kifogásolható.

 

Ezt a vetületet 1923-ban J. P. Goode amerikai kartográfus publikálta. (A határoló szélességet a ±40°44’ = ±40.7333…° értékkel közelítette.) Vetületének különlegessége, hogy a térképen több kezdőmeridiánt is felvett a fontosabb kontinensek középvonalában (???.ábra). Ennek következtében az óceánokon szakadások léptek fel. Később ezt a megoldást a tematikához alkalmazkodva alkalmazták más vetületeknél és más kezdőmeridiánokkal is.

 

 

Érdi-Krausz féle vetület

 

A Goode féle vetület alapötletet fejlesztette tovább Érdi-Krausz György. A középső sávot a Mercator-sor megfelelő tagjával képezte le, míg a pólusok környékét ő is Mollweide féle vetületben ábrázolta; a határoló szélességet vagy a jH=±60°, vagy a jH=±70° parallelkörre javasolta. A Mercator-sor paramétereinek meghatározásakor a p=0.4 és q=0.6 értékből indult ki, ami az  m=0.8  és  n=0.737918  értéket eredményezte. Ha tehát ½j½£jH , az alábbi vetületi egyenletek érvényesek:

 

A Mollweide féle vetületben mind a ±60°, mind a ±70° szélességi körök hossza rövidebb lesz, mint a Mercator-Sanson féle vetületben. Ezért a sávok összeillesztése céljából a Mollweide vetületben készült sávokon egy hasonlósági transzformációt hajtunk végre. Ennek aránya jH=±60° (yH=±49.6750°)  esetén cH=1.188719, míg jH=±70° (yH=±59.5317°)  esetén cH=1.387333. A vetületi egyenletek e sávokon:

 

jH=±60° választásakor

  és

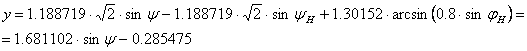
(Az  y  vetületi egyenlet  j³0 esetre vonatkozik; negatív j-nél az első tag változatlan, a többi tag előjele megváltozik.)

 

jH=±70° választásakor

  és

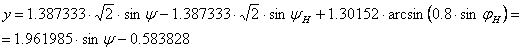
(Az előző választáshoz hasonlóan az  y  vetületi egyenlet itt is a  j³0 esetre vonatkozik; negatív j-nél az első tag változatlan, a többi tag előjele megváltozik.)

 

A sávok összeillesztése csak a meridiánok folytonosságát jelenti, a folytonos differenciálhatóságát nem. Ennek megfelelően a meridiánok a határoló szélességeken kissé megtörnek.

 

Érdi-Krausz szerint a cH-szoros  nagyítás felfogható a méretarány nagyításaként is, ezért az e vetületben készült térképein két névleges méretarány van feltüntetve: egy a ½j½£jH , egy másik pedig a ½j½>jH  gömbövre. E felfogás mellett a vetület minden sávon belül területtartónak tekinthető.

 

Az Érdi-Krausz féle vetülettel, melynek leírása 1968-ból származik,  a magyar atlaszkartográfia világtérképein találkozhatunk.

 

 

Baranyi II. vetülete

 

Ez a vetület egy fokhálózat-szerkesztési leíráson alapszik, mely szerint a világtérkép kontúrját alkotó határoló meridiánok olyan körívekből állnak, amelyek egymáshoz a jH=±70° szélességnél törésmentesen csatlakoznak. Az alsó és felső (nagyobb sugarú) körív középpontja a középmeridiánon, a jobb és baloldali (kisebb sugarú) körív középpontja az egyenlítőn helyezkedik el.

 

A szélességi körök ekvidisztánsak, az egyenlítő hossztartó. A középmeridián ymax hossza az egyenlítő hosszának 0.7-szerese, rajta az osztásközök az egyenlítőtől a pólusok felé egyenletesen növekednek. A ±70° szélesség az egyenlítő és a pólusok közötti távolságot 13:5 arányban osztja fel (???. ábra). E feltételekből meghatározható a másodfokú y=y(j) vetületi egyenlet:

 

A továbbiakhoz határozzuk meg a ±70° szélességi kör képének 2d hosszát, a kontúrvonal csatlakozási pontjához vezető rádiuszvektornak az egyenlítővel bezárt d szögét, valamint e rádiuszvektor (egyben az oldalsó határoló körív) r1 hosszát. Az ábráról leolvasható, hogy

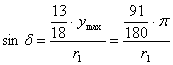   vagyis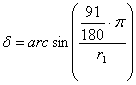  

és  

 

Másrészt az oldalsó és felső határoló körív törésmentes csatlakozásából következik, hogy a csatlakozási ponthoz vezető két rádiuszvektor egybeesik, vagyis a nagyobbik (r2 hosszúságú) rádiuszvektor a középmeridiánnal  h=90°-d  szöget zár be. A pólust a csatlakozási ponttal összekötő egyenes szakasz a d hosszúságú elválasztó fél-parallelkörrel és a középmeridián megfelelő darabjával együtt egy derékszögű háromszöget alkot, melynek a csatlakozási pontnál lévő szöge (a merőleges szárú szögek miatt) éppen h/2 nagyságú. Innen következik:

 

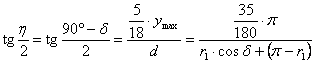
Ebből az egyenletből kifejezhető d:

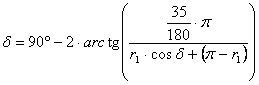
A d két alakja egymással egyenlővé tehető:

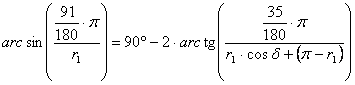
Megoldva ezt a nem-lineáris egyenletet:   r1=1.84466

Visszahelyettesítve a fenti egyenletekbe, kapjuk:   d=59.42867°   és   d=2.23514,  továbbá ,  ami alig tér el a középmeridián hosszától (4.39823).

 

Jelöljük ½j½£jH  esetén a  j  szélességi kör oldalsó határoló körívvel való metszéspontjához vezető rádiuszvektornak az egyenlítővel bezárt szögét  y-vel, ½j½>jH  esetén pedig a j  szélességi kör felső határoló körívvel való metszéspontjához vezető rádiuszvektornak a középmeridiánnal bezárt szögét z-val.

 

Ha  ½j½£jH,  akkor a szélességi kör felének hossza ,  tehát  , ahol y az 

egyenletből határozható meg.

 

Ha  ½j½>jH,  akkor a szélességi kör felének hossza ,  tehát

,  ahol  z  az

egyenletből adódik.

 

A meridiánívek a határoló meridiánok affin képei, tehát egymáshoz törésmentesen csatlakozó ellipszisívekből állnak.

 

A  h  és  ctgq  fokhálózatmenti torzulások képlete is függ a  j  szélesség és a ±jH  határoló szélességek viszonyától:

 

½j½£jH  esetén    és 

½j½>jH  esetén    és  

Végül

 

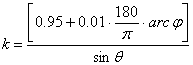
Innen látható, hogy a vetület általános torzulású. A szögtorzulások csak a pólusoknál és a kontúrvonal egyenlítőtől távolabb eső környezetében jelentősek, ezért a kontinensek alakja kevésé torzul. A területtorzulások a magasabb szélességeken gyorsan nőnek.

 

Baranyi II. vetülete 1968-ban nyert publicitást. A 70-es évektől magyar atlaszokban (elsősorban történelmi témájú világtérképekhez) használják. E térképeken a középmeridián általában a 10° K-i hosszúsági körre esik, hogy a határoló meridián minél kevesebb szárazulatot vágjon ketté.

 

 

Baranyi IV. vetülete

 

A vetület eredeti szerkesztési leírása csak rajzi méreteket ad, az alapfelületi méretekkel való kapcsolatra nem utal. A kontúrvonal megadása hasonló a II. vetületéhez, azzal a különbséggel, hogy az egyenlítő és a középmeridián térképi hosszán (368 illetve 222 egység) kívül most az oldalsó határoló körív sugara adott: r1=100 egység. A kontúrmeridiánt alkotó körívek törésmentes csatlakozásából következik (ld. ???. ábra), hogy a felső határoló körív sugarát r2-vel jelölve, egy  (r2-100) szárhosszúságú szimmetrikus háromszöget kapunk. A merőleges szárú szögekből adódik, hogy (b-val jelölve a csúcsszöget)

Ebből  b=14.92°,  a=75.08°  és  r2=426.23  következik.

 

A 10 fokonként vett szélességi körök képének egymástól való távolsága az egyenlítő és a pólusok 30°-os környezetében 12 egység, míg a közepes szélességeknél (30°-60°) 13 egység. A megadott értékekhez kilencedfokú függvény illeszthető, amely biztosítja a parallelkörök távolságának folytonos függvény szerinti változását  –  ±45°-ig e távolságok növekedését, onnan a pólusokig e távolságok csökkenését. Ezek alapján:

(Megjegyezzük, hogy  y  megadható az eggyel kevesebb együtthatót tartalmazó, de a szerkesztési eljárás méreteit valamivel kevésbé hatékonyan reprodukáló

vetületi egyenlettel is.)

 

A kontúrkörívek csatlakozási pontjának távolsága az  x  tengelytől 96.63 egység, ebből meghatározható a csatlakozási pont szélessége: ±78.07°.

 

A meridiánok az egyenlítőt a térképen nem egyenközűen metszik; az osztásközök nagysága a középmeridián felől a kontúrmeridián felé haladva a szerkesztési utasítás szerint csökken:  egység. Minthogy ugyanilyen arányban metszik a meridiánok a többi szélességi kört is, elegendő a csökkenés jellegét visszaadó függvényt egyszer előállítani. Ez egy logaritmus-függvény:

Az adott szélességen érvényes x vetületi egyenletet a f(l) függvénynek a félparallelkörök hosszával való beszorzásából kapjuk:

½j½£78.07°  esetén 

½j½>78.07°  esetén 

A meridiánívek – hasonlóan Baranyi II. vetületéhez - a határoló meridiánok affin képei, tehát itt is egymáshoz törésmentesen csatlakozó három ellipszisívből állnak.

 

A fokhálózat menti torzulások:

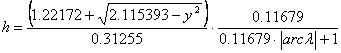,  ha  ½j½£78.07°,

és  

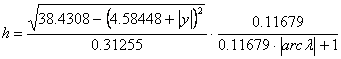,  ha  ½j½>78.07°

továbbá

 , 

ahol 

 ,

végül 

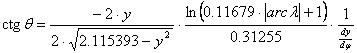,  ha  ½j½£78.07°,

és 

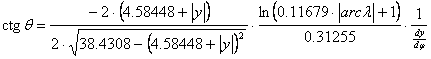 , ha  ½j½>78.07°

 

Ezekből nyilvánvaló, hogy ez az 1968-ban publikált vetület általános torzulású. A kontinensek alakja csak kis mértékben torzul. Alkalmazása minden olyan világtérképhez előnyös, ahol a területtartás nem követelmény. A mérsékelt égövi területek kismértékű É-D irányú megnyújtása a gazdasági tematikus térképek számára hasznos, de a magyar geokartográfiában más témák ábrázolására is használják. A középmeridián a legtöbb alkalmazásnál itt is a 10° K-i hosszúsági körre kerül, de előfordul más (pl. 150° K-i hosszúságú) középmeridiánnal is.

 

 

Osztott Baranyi-vetület (Baranyi IV. vetületének osztott változata)

 

A világvetületek többnyire a szárazföldekhez kötődő témák bemutatását szolgálják, és ezt többé-kevésbé előnyösen meg is valósítják. A világtenger ill. az óceánok ábrázolása szempontjából azonban inkább hátrányosak, ezért merült fel – Goode vetületének egyik alapötletét alkalmazva – több középmeridián felvétele, éspedig az óceánok középvonalában.

 

E vetületben az ábrázolás két középmeridiánnal és két, a féltekénél valamivel nagyobb területen történik. A bal oldali területrészen az Atlanti- és az Indiai-óceán jelenik meg a 10° K-i hosszúságú középmeridiánnal, melyen a vetületi egyenletek a 100° Ny-i hosszúságtól a 100° K-i hosszúságig érvényesek. A jobb oldali területrész középmeridiánja a 160° Ny-i hosszúsági kör; ezzel a középmeridiánnal a vetületi egyenletek a 140° K-i és a 60° Ny-i hosszúság közé eső zónát adják meg. A két területrész között (tehát a 100° és 140° K-i hosszúság által határolt gömbkétszögön) egy átmeneti zóna van, amely az É-i félgömbön a jobb oldali területrésszel, a déli félgömbön a bal oldali területrésszel függ össze, ez utóbbinál a 35° D-i szélességtől délre a 140° és 150° K-i hosszúság közötti zóna biztosít átfedést a két óceán földrajzi határán fekvő Tasmánia számára (???ábra).

 

A bal és jobb oldali területrész ilyen összekapcsolása annyiban jelent nehézséget, hogy az  x  vetületi egyenletből adódó Egyenlítő menti hossztorzulás a bal oldali területrész esetében Ny-ról K felé, a jobb oldali területrész esetén pedig K-ről Ny felé csökkenne, emiatt viszont az összeillesztésnél a meridiánok az Egyenlítőn megszakadhatnának. A meridiánok folytonossága érdekében az átmeneti zónában az  x  vetületi egyenletet megváltoztattuk egy olyan, Dl-ban másodfokú függvényre, amelynek Dl szerinti deriváltja a 100° K-i hosszúságnál a bal oldali területrész megfelelő értékével, a 140° K-i hosszúságnál pedig a jobb oldali területrész megfelelő értékével egyezik meg. A derivált így a teljes Egyenlítő mentén folytonos, a többi parallelkör mentén pedig a szakadási meridiánok kivételével a folytonosság szintén teljesül. Ez biztosítja a vetületi torzulások folytonos változását a csatlakozásoknál.

 

A vetület matematikai leírásánál induljunk ki a Baranyi IV. vetületének fentiekben megadott egyenleteiből. Tehát

vagy az egyszerűbb, de kevésbé pontos képlettel

 

A bal oldali területrészen, vagyis ha

            ,

akkor  ½j½£78,07°  esetén  

 ,

míg  ½j½>78,07°  esetén  

ahol  Dl= l-lk ,  és  lk=10° K  a középmeridián hosszúsága.

 

A jobb oldali területrészen, vagyis ha

             ,

akkor  ½j½£78,07°  esetén  

 ,

míg  ½j½>78,07°  esetén  

 ,

ahol  Dl= l-lk ,  és  lk=160° Ny  a középmeridián hosszúsága; továbbá

            ,

ami biztosítja a két középmeridián megfelelő távolságát.

 

Az átmeneti zóna déli félgömbre (j <0°) eső részének előállítása (ahol a bal oldali területrészhez kapcsolódás miatt  lk=10° K):

j £ -78,07°  esetén  

             ,

j > -78,07°  esetén pedig

              .

(A Tasmánia számára létrehozott átfedési zónában ezek a képletek a  -35°£j£0° övezetben a  90°£Dl£130°  közötti sávra, a  -90°£j£-35°  övezetben pedig a  90°£Dl£130°  közötti sávra érvényesek.)

 

Az átmeneti zóna északi félgömbre (j ³0°) eső részének előállítása (ahol a jobb oldali területrészhez kapcsolódás miatt  lk=160° Ny):

j £ 78,07°  esetén

 

,

j > 78,07°  esetén pedig       

.

(Mindkét képlet  -100°£Dl£-60°  között érvényes.)

 

A magyar földrajzi gyakorlatban nem óceánként kezelt Északi-Jeges-tengert egy melléktérképen lehet jó alaktartással ábrázolni, amely behelyezhető az É-i megszakított részre, Ázsia részbeni  elfedésével. A kör alakú melléktérkép Postel vetületben készül, a pólus képe a körben excentrikusan helyezkedik el. A vetületi egyenletek:

           

           

ahol (xt,yt) a Baranyi féle vetület koordinátarendszerének origójához képesti eltolás, melynek ajánlott értékei:

           

           

A melléktérkép kör alakú, melynek  r  sugara egy 32°-os meridiánív hosszával egyenlő:

 ,

középpontja azonban nem a pólussal esik egybe, hanem a 81° É-i szélesség és a 90° Ny-i hosszúság által meghatározott pontban van, melynek  (xr,yr)  koordinátái:

             

             .

A kontúrkör egyenlete tehát:

            ,

amely így összefüggően és előnyös torzulásokkal tartalmazza a Hudson-öböltől az Ob-öbölig terjedőleg az Északi-sarki-óceán teljes területét (???ábra).

 

A vetület torzulásait a Baranyi IV. vetületénél megadott képletek alapján lehet kiszámítani úgy, hogy  l  helyett  Dl -t írunk, és a  Dl= l-lk –ban szereplő  lk  értékét a bal oldali területrészen 10° K-i, a jobb oldali területrészen pedig  160° Ny-i hosszúságnak választjuk.

 

E vetületet Márton Mátyás fejlesztette ki 1986-tól több lépcsőben.

 

 

Robinson vetülete

 

Robinson a vetület megkonstruálásában Baranyi elveit követte, amennyiben a fokhálózatot szerkesztés útján hozta létre, és a kontinensek alakjainak torzulását minél kisebbre igyekezett csökkenteni. Az 1974-ben táblázatos formában közölt vetület pólusvonalas; a parallelkörök ekvidisztánsak.

 

Ehhez a fokhálózathoz 1991-ben Beineke készített analitikus formájú vetületi egyenleteket:

ahol                 a=0.96047                  e=-0.3670

                        b=-0.00857                f=-0.1500

                        c=6.4100                    g=0.0379

                        d=2.6666

 

A fokhálózat menti torzulások:

,  ahol

 

 

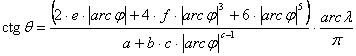
Látható, hogy a vetület általános torzulású. Főleg az Egyesült Államokban készült világtérképek vetületeként használják.

 

 

Képzetes hengervetületek egyenes vonalú meridiánképekkel

 

 

Donis vetülete

 

A vetület póluspontos, középmeridiánban és egyenlítőben hossztartó. Ennek alapján a vetületi egyenletek:

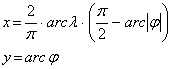
Innen a fokhálózat menti torzulások:

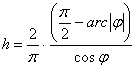
A vetület tehát általános torzulású, a parallelkörök ekvidisztánsak. Az abszolút érték miatt az  x  vetületi egyenlet különbözik az É-i és a D-i félgömbön, ezért összetett vetületnek tekinthetjük. Az egyenlítő mentén a hosszúsági körök megtörnek. A teljes Föld képe rombusz kontúrban jelenik meg. 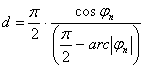Ha az egyenlítő helyett a  ±jn  szélességi kört akarjuk hossztartónak, akkor az  x  vetületi egyenletet  be kell szorozni a    egyenletből adódó  -vel.

 

Donis vetülete a XV. századból ered. Ritkán használták világtérképekhez, inkább foktrapéz alakú területeket ábrázoltak síktrapéz formájában.

 

Collignon vetülete

 

Készítsünk póluspontos, területtartó képzetes hengervetületet egyenes vonalú meridiánképekkel a Donis féle vetületből a módosított földrajzi szélesség bevezetése révén. Először is hajtsunk végre c arányú hasonlósági transzformációt a rombusz alakú teljes Föld területegyenlő leképezése érdekében. Minthogy Donis vetületében a teljes Föld képének területe  ,  a hasonlósági transzformáció után a    egyenletet kapjuk, ahonnan  . 

A vetületi egyenletek a  y  módosított szélesség bevezetése után:

 

 

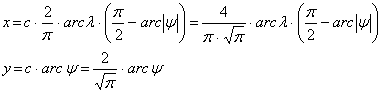
Teljesüljön a területegyenlőség minden, az egyenlítő és a  j  szélességi kör által határolt gömbövre (???. ábra):

 

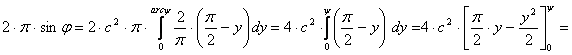
A  y  és  j  közötti összefüggés tehát egy y-ben másodfokú egyenlet:

Ennek megoldása:

Az  arcy  nem lehet p/2 –nél nagyobb, ezért a megoldásban csak negatív előjel szerepelhet. Vagyis:

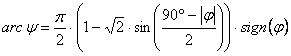
Ezek szerint a végleges vetületi egyenletek:

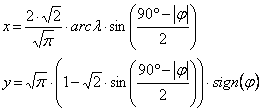
A fokhálózatmenti torzulások:

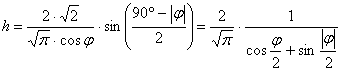
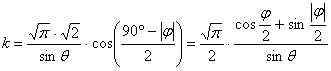
A vetület tehát valóban területtartó, emellett parallelkörökben ekvidisztáns. A meridiánok az egyenlítőn itt is megtörnek.

Ha az egyenlítő helyett a  ±jn  szélességi kört akarjuk hossztartónak, akkor az  x  vetületi egyenletet  be kell szorozni a    egyenletből adódó  -vel, az y  vetületi egyenletet pedig  d-vel kell osztani.

 

 

Collignon vetülete 1865-ban keletkezett. Ritkán alkalmazzák ország vagy kontinens méretű (az egyenlítőt lehetőleg nem tartalmazó) terület, esetleg a teljes Föld területtartó ábrázolására.

 

 

Eckert I. vetülete

 

Készítsük el a négyzetes hengervetület    és a Donis féle vetület    keverékét:

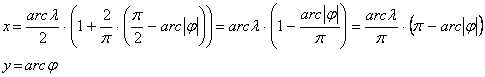
A fokhálózat menti torzulások:

Ez Eckert I. vetülete, amely 1906-ból származik. Az egyenlítő és a középmeridián – szemben a III. és V. vetülettel - hossztartó, a többi parallelkör ekvidisztáns. Általános torzulású. Korábban a teljes Föld megjelenítésére használták.

 

 

Eckert II. vetülete

 

Készítsünk területtartó vetületet Eckert I. vetületéből módosított földrajzi szélesség bevezetésével. Ehhez először a teljes Földre vonatkozó területegyenlő leképezést kell megvalósítani, ami – minthogy a teljes Föld képének fokhálózata egy négyzetre és két egyenlő szárú derékszögű háromszögre bontható fel (???. ábra) - egy c-szeres hasonlósági transzformáció végrehajtása után a   egyenletet eredményezi. Innen 

 

A  y  módosított szélesség bevezetése után a  y(j)  összefüggés az egyenlítő által határolt gömbövek területegyenlő leképezéséből adódik:

 

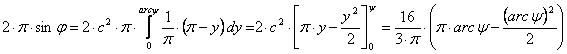
A  y  és  j  közötti összefüggés tehát itt is egy y-ben másodfokú egyenlet:

Ennek megoldása:

Az  arcy  nem lehet p –nél nagyobb, ezért a megoldásban csak negatív előjel szerepelhet. Vagyis:

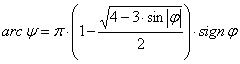
Ezek szerint a végleges vetületi egyenletek:

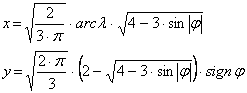
A fokhálózatmenti torzulások:

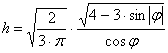
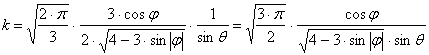
A vetület tehát valóban területtartó, továbbá parallelkörökben ekvidisztáns. A meridiánok az egyenlítőn megtörnek.

Eckert 1906-ban publikált II. vetületét területtartó világtérképek vetületeként elvétve ma is használják.

 

 

Egyéb képzetes hengervetületek

 

 

Loximutális vetület

 

Készítsünk vetületet, amely egy meghatározott Pn(jn,ln) pontból kiinduló loxodrómákat olyan hossztartó egyenesekre képezi le, amelyeknek egymással bezárt szöge megegyezik a loxodrómák  

által a Pn pontban bezárt alapfelületi szöggel (vagyis a loxodrómákra nézve „azimutális”). Egy ilyen vetületben a  ln  meridián mint speciális loxodróma képe hossztartó egyenes lesz, amely a fokhálózat szimmetriatengelye. Hasonlóan a  jn  parallelkör képe is hossztartó egyenes, mely merőleges az előbbire, és  jn=0°  esetén szintén szimmetriatengely.

 

Legyen a fenti két egyenes a síkkoordinátarendszer  y  és  x  tengelye. Ismeretes, hogy a  Pn(jn,ln)  és  P(j,l)  pontokat összekötő loxodróma egyenlete:

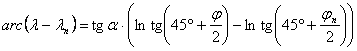
ahol  a  a loxodrómának a meridiánokkal bezárt azimutja. Tudjuk továbbá, hogy a loxodróma  Pn   és  P  közötti  s  ívhossza az 

 

képlettel számítható, kivéve a  j=jn  esetet, amikor is a loxodróma éppen egy parallelkör, és   .

 

A  P(j,l)  pont képének síkkoordinátái  j¹jn   esetén (???. ábra):

 

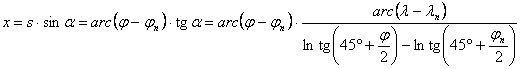
Ha viszont  j=jn,  akkor

 

Az  y  vetületi egyenlet csak  j-től függ, az  x  viszont mind  j-től, mind  l-tól; ez a vetület tehát valóban képzetes hengervetület.

 

A fokhálózatmenti hossztorzulások  j¹jn   esetén :

 

 

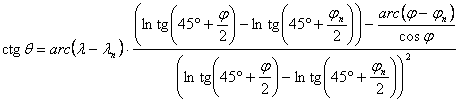
Ha  j=jn,  akkor

A loximutális vetület tehát általános torzulású, parallelkörei ekvidisztánsak, a  jn  szélességi kör és a középmeridián hossztartó. A fokhálózat általában nem szimmetrikus az egyenlítőre, kivéve a  jn=0 esetet.

 

Ezt a vetületet Siemon német kartográfus publikálta 1935-ben. A „loximutális” elnevezés Tobler amerikai térképésztől származik (1966).