KÉPZETES KÚPVETÜLETEK
A
képzetes kúpvetületeknél a (segéd-) parallelkörök képei körívek (nem
szükségszerűen koncentrikusak), a (segéd-) meridiánok képei tetszőleges
törvényszerűséget követő vonalak. A valódi kúpvetületekhez hasonlóan a
koordinátarendszer y tengelye a középmeridián képe, és egyben a fokhálózat
szimmetriatengelye. Az x=x(j,l) vetületi egyenlet
tehát l-ban páratlan.
Egy
adott j,l koordinátájú pont térképi síkkoordinátáit a
képletekkel
adhatjuk meg (ld. ??? ábra), ahol
-
a j szélességi kör sugara (a sugárfüggvény), mely
a j -nek
szigorúan monoton csökkenő függvénye;
-
a j szélességi kör középpontjának távolsága
az x tengelytől.
-
a j,l koordinátájú pont képéhez vezető
rádiuszvektornak a középmeridiánnal bezárt szöge, mely a l-nak páratlan, szigorúan monoton
növekedő függvénye, és legyen
(vagyis l=0 jelentse a középmeridiánt).
A fokhálózat menti torzulások közül először a h parallelkör menti hossztorzulást írjuk fel:
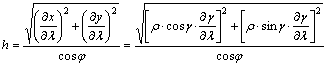
vagyis
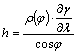
A
fokhálózati vonalak által bezárt Q szögre:
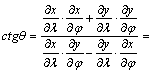
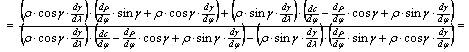
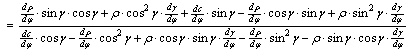
(Közben
elvégeztünk egy egyszerűsítést, feltételezve, hogy 
.) Az összevonások után kapjuk, hogy
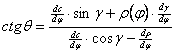
Ebből
következik, hogy
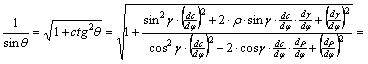
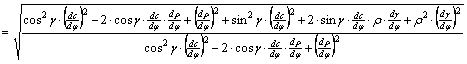
Az
összevonások után tehát
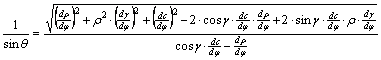
A
meridián menti k hossztorzulás:
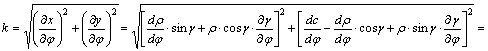
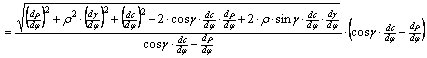
Felhasználva
az iménti egyenlőséget:
A
területtorzulási modulus:
A
foktrapéz képének területe:
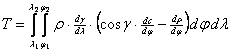
Igazi képzetes kúpvetületek
A
képzetes kúpvetületeknél a parallelkörök körív alakú képeinek középpontjairól
általában csak annyit kötünk ki, hogy a középmeridiánon helyezkedjenek el.
Azokat viszont, amelyeknél a parallelkörök képei koncentrikus körívek, igazi képzetes kúpvetületeknek nevezzük.
Ezeknél c=c(j) konstans. A fokhálózat menti torzulásokat
tehát az alábbi, az általánosnál egyszerűbb képletek adják:
, 
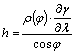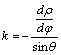és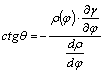 
;
ezekből
adódik a területtorzulási modulus:
A
meridiánok képei most nem lehetnek egy ponton áthaladó egyenesek, ezért a
fokhálózati vonalak általában nem merőlegesek egymásra. Emiatt az igazi
képzetes kúpvetületek között
nincsenek
szögtartók.
Bonne vetülete
Bonne vetülete olyan igazi képzetes kúpvetület, melynél a parallelkörök és
középmeridián mentén hossztartást követelünk meg: h=1
és 
A
középmeridián menti hossztartás képletben felírva:
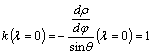
Ebből (figyelembe véve, hogy a középmeridián mentén
a fokhálózati szimmetria miatt q=90°) következik, hogy
,
vagyis
ahol d integrációs konstans. Ennek meghatározásához
nevezzünk ki a jn szélességi
kört „normálparallelkörnek”, amelyre előírjuk, hogy –
a minden parallelkörre érvényes hossztartáson túl – rendelkezzen az egy
parallelkörben hossztartó valódi
kúpvetületek normálparallelkörének azon
tulajdonságával, mely szerint
.
Ez
a pótlólagos feltétel megszabja a d
integrációs konstanst:
A
sugárfüggvény tehát:
.
A
vetületünk póluspontos, a pólus képe nem a parallelkörök közös középpontjába
esik.
A
parallelkörök mentén előírt hossztartás:
;
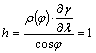ebből
adódik, hogy
,
tehát
A g szög tehát arányos a l hosszúsággal, amelynek
együtthatója
a valódi kúpvetületek n
sugárhajlásához hasonló, de a j szélességtől függő mennyiség. Megjegyezzük,
hogy a j=jn
helyettesítés után
,
vagyis
a vetületünk „normálparallelköre” mentén fennáll
a jn szélességi körön hossztartó valódi
kúpvetületek másik tulajdonsága is, mely szerint
.
A „normálparallelkör” a hossztartáson túl további speciális
torzulási tulajdonságokkal is bír. Vizsgáljuk meg a meridiánokkal bezárt q szögét.
A ctgq az általános képletből r és g behelyettesítése és egyszerűsítés után:
Ennek
értéke j=jn behelyettesítése után:
A „normálparallelkör” tehát a meridiánokkal derékszöget zár
be, emiatt a fokhálózati vonalak iránya itt vetületi főirány.
Ugyanitt
a meridián menti hossztorzulás (felhasználva a q szög merőlegességét is):
A
vetületi főirányokban hossztartás áll fenn, ami a jn parallelkör torzulásmentességét jelenti,
vagyis jogos a „normálparallelkör” megjelölés.
A
területtorzulási modulus:
,
vagyis
a Bonne féle vetület területtartó.
A
Föld Bonne vetületében (jn=45°) a ??? ábrán látható.
A Bonne féle vetület alapgondolata már Ptolmaiosnál
megtalálható. A XVI. századi újrafelfedezését követően a vetületet Bonne francia mérnök és geográfus alkalmazta 1752-ben. A XIX.sz.-ban elterjedten használták a topokartográfiában,
így pl. Franciaország 1:80000 méretarányú katonai térképéhez. (Innen ered a vetület "Carte de
France" elnevezése.) A XX.sz.-ban a geokartográfiai alkalmazásai kerültek előtérbe, közepes
szélességeken elterülő kontinensek, kontinensrészek, nagyobb országok
területtartó ábrázolásánál.
A
különböző normálszélességű Bonne féle vetületek közül
nevezetes a jn=90°-hoz tartozó Werner féle "cardioid" (szívalakú) vetület (1514), amelyet egy későbbi alkalmazójáról Stab (Stabius) féle vetületnek is
neveznek (1517). Másrészt jn ® 0° esetén határhelyzetben a Mercator-Sanson féle vetületet kapjuk meg.
Polikónikus vetületek
A polikónikus vetületek eredeztetési alapelvének megértéséhez
először ábrázoljuk pl. az É-i félgömböt egyetlen érintő perspektív kúpvetületben. Ekkor
a jn érintési parallelkör, melynek sugara a
kiterítés utáni síkon
,
torzulásmentes;
a torzulások ettől a szélességtől a pólus illetve az egyenlítő felé haladva
eleinte lassan, majd gyorsulva növekednek. A félgömb ábrázolása során fellépő
nagymértékű torzulásokat csökkenthetjük pl. úgy, hogy szélességi körökkel mind
több gömbövre bontjuk, és minden egyes gömbövön olyan perspektív
kúpvetületet alkalmazunk, mely a szóban forgó gömböv középvonalát érinti (ld.
??? ábra). A térképen viszont az egyes gömbövek határánál szakadások lépnek
fel. A gyarapodó számú érintési parallelkör környezetében a torzulások kicsik
maradnak, a keskenyedő gömböveken így egyre kevésbé nőnek meg a torzulások, a
szakadások egyre keskenyebbé válnak.
A
gömbövekre való felosztást minden határon túl folytatva, végül minden egyes szélességi kör térképi
sugara az adott szélességen érintő normálparallelkör sugarával fog megegyezni, továbbá a
szakadások végtelenül keskennyé válva elenyésznek,
így a félgömb egy összefüggő síkidomra képeződik le.
A
fenti alapelvből származik a definíció: a
polikónikus vetületek olyan képzetes kúpvetületek,
amelyeknél j³0 esetén a r sugárfüggvényt a
képlet adja meg.
További
tulajdonságként előírható, hogy a középmeridián ekvidisztáns
legyen, ami képletben:
(ahol
a d>0 állandó adja a középmeridián menti
hossztorzulást, ami d=1 esetén a középmeridián
hossztartását jelenti).
A g=g(j,l)-ra, amely szigorúan monoton növő, páratlan
függvénye l-nak, teljesüljenek az alábbi
határérték-követelmények:
(vagyis
l=0 jelentse a középmeridiánt), továbbá
és
(vagyis
az egyenlítő határhelyzetben ábrázolható, és az
y=0 egyenesre képeződik le).
A
teljes Föld ábrázolása a külön-külön ábrázolt félgömböknek az egyenlítő mentén
való összeillesztése útján lehetséges. (A D-i félgömb ábrázolásához
helyettesítsünk a fenti képletekbe j helyett
mindenütt |j| -et, és az y
koordinátát szorozzuk be sign(j)-vel.)
Megjegyezzük,
hogy az x tengely önmagával párhuzamosan eltolható, úgy
hogy pl. az ábrázolandó területen áthaladó
jn szélességi
kört érintse, amikor is a c=c(j) függvény
alakot
ölt.
Közönséges vagy amerikai polikónikus
vetület
A
középmeridián ekvidisztáns, azaz
A
parallelkörök mentén hossztartást követelünk meg, vagyis:
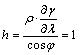
Az
egyenletet átrendezve, kapjuk:
,
ahonnan
következik
(az
integrációs konstans a g -ra
tett feltétel miatt csak zérus lehet).
Felhasználva,
hogy
és
,
kapjuk
a fokhálózat menti torzulásokat:
,
tehát 
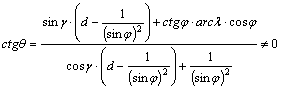
Minthogy
a vetület sem területtartó, sem szögtartó nem lehet, tehát általános torzulású.
A
??? ábra a két félgömb összeillesztett képét ábrázolja egyszerű polikónikus vetületben.
A
vetületet 1820-ban Hassler amerikai térképész alkotta meg. Az Egyesült Államokban
a XIX. században topográfiai térképek
vetületeként használták. Az amerikai geokartográfiában
a transzverzális változat is előfordul.
Ortogonális
polikónikus
vetület
A
fokhálózati vonalak merőlegessége (ortogonalitása)
matematikailag a
egyenlettel
fogalmazható meg. Másrészt tudjuk, hogy a polikónikus
vetületeknél
,
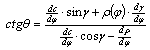a
két egyenletből adódik
.
Kifejezve 
-t
, kapjuk:
.
Behelyettesítve
ide a
és
a
egyenlőségeket:
,
ami
egy szétválasztható változójú differenciálegyenlet. Ezt megoldva:
Elvégezve
az integrálást:
,
ahol f(l) integrációs konstans, mely l-nak tetszőleges szigorúan
monoton növekedő függvénye, és
.
A
tagokat összevonva:
,
majd
;
végül
.
d=1 esetén:
Ha
,
akkor
kapjuk:
amelyet
"War Office" vetület néven Nagy
Britanniában használtak a XIX. században nagyméretarányú katonai topográfiai
térképekhez.
Határozzuk
meg a "War Office" vetület fokhálózat menti
torzulását:
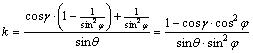
Nyilvánvaló,
hogy h¹k és hAkAsinq ¹1 , ezért a vetület általános torzulású. j®0
esetén h®1, vagyis az egyenlítő határhelyzetben
hossztartó.
A
??? ábráról leolvashatóan az AB egyenes a
g nagyságú AOC szög felezője, tehát
;
másrészt
a fentiek szerint
.
A
két egyenlőségből kapjuk, hogy
.
A
körhöz külső pontból húzott két érintő egyenlősége miatt a térképen, a
középmeridiánra emelt merőlegesen kijelölve a B pontot, az O középpontú és r=ctgj sugarú kör kerületén körzővel kijelölhetjük a
B ponttól AB távolságra lévő, a r(j), g(j,l) polárkoordinátákkal
jellemzett C pontot. Ez a módszer megkönnyíti a fokhálózat
geometriai megszerkesztését.
A
??? ábra a két összeillesztett félgömb képét mutatja ortogonális polikónikus vetületben.
Területtartó polikónikus
vetület
A
területtartás alapegyenlete
,
ami
polikónikus vetületek esetén
.
Integráljuk
az egyenlet mindkét oldalát l szerint:
ahol t(j) az integrációs konstans, amely függhet j -től.
A baloldal g -n keresztül függ l-tól, ezért azt g szerint integrálva:
l=0 esetén teljesülnie kell g=0 –nak,
ebből adódóan t(j)º0 .
Felhasználva,
hogy r=ctgj , 
, továbbá , kapjuk:
majd
egyszerűsítés után átszorozva sin3j-vel:
,
ami g implicit függvénye; adott j és l esetén ez egy
g -ban nemlineáris egyenlet, amely közelítéssel oldható
meg.
A
középmeridián hossztartása, vagyis d=1
esetén az összefüggés a következő alakú:
A
két félgömb ezzel a képlettel számolt képe összeillesztve látható a ??? ábrán.
A fokhálózat merőlegessége szükséges a
szögtartáshoz. Ha ehhez még a középmeridián ekvidisztanciáját
is előírjuk, akkor a fentiekben ismertetett ortogonális polikónikus
vetületet kapjuk, amely - mint emlékezetes - általános torzulású, vagyis nem
szögtartó. Ha viszont a sugárfüggvényre vonatkozó p=ctgj feltétel megtartása mellett a középmeridián
mentén tetszőleges hossztorzulást megengedünk, akkor már létrehozható szögtartó
polikónikus vetület.
A
levezetés mellőzésével a szögtartó polikónikus
vetület jellemző függvényei az alábbiak:
,
,
és
,
vagyis
A
középmeridián és az egyenlítő mentén az osztásközök a vetületi kezdőponttól
távolodva nőnek. A vetület a gömböt a teljes síkra képezi le, ezért félgömbnél
nagyobb terület ábrázolásakor rohamosan növő hossz- és területtorzulásokkal
kell számolni.
A
félgömb képét a ???. ábra mutatja.
Pszeudopolikónikus vetületek
A pszeudopolikónikus vetületeknél a parallelkörök képei (nem
szükségszerűen koncentrikus) körívek, de - ellentétben a polikónikus
vetületekkel - a r sugárfüggvény a j-nek tetszőleges szigorúan monoton csökkenő függvénye lehet. A
meridiánok képei általában valamilyen görbe vonalak.
Az
elméletileg elképzelhető nagy számú pszeudopolikónikus
vetület közül a gyakorlatban főleg olyanok fordulnak elő, amelyeknél a meridiánok képei is körívek. Ezt a
vetületsokaságot "Lagrange féle vetületcsalád"-nak nevezik.
Kifejlesztésüket a XVII. századtól kezdve az motiválta, hogy a térképhez a
csupa körívből álló fokhálózat geometriailag könnyen volt megszerkeszthető.
Lagrange vetülete
Készítsünk
szögtartó pszeudopolikónikus
vetületet körív alakú meridiánképekkel. A szögtartás követelményét enyhítsük
azzal az előírással, hogy a pólusoknál mint szinguláris pontoknál csak a
meridiánok által bezárt szög arányos leképeződését írjuk elő. Ez utóbbi
feltételt – bevezetve a l meridián képe pólusbeli érintőjének a középmeridián
képével (az y tengellyel) bezárt szögére a l’ jelölést (???ábra) – a
képlet
adja meg, ahol k a vetületet jellemző konstans. Legyen az
egyenlítő képe az x tengely, és kerüljön a
pólusok képe a (0,p/2) és
a (0,-p/2) koordinátájú pontokba. Ha k³0.5, akkor a térképen
biztosan lesz két félkör alakú meridián, amelyek együtt egy p/2 sugarú kört alkotnak.
Jelölje C1(x1,0) a l meridiánkép
középpontját. Az N pólushoz vezető rm
rádiuszvektor az x
tengellyel k@l szöget zár be (merőleges szárú szögek),
továbbá az OC1N derékszögű
háromszögből
és
.
A
hosszúsági körök síkbeli egyenlete tehát:
A j szélességi kör képének középpontja legyen C2(0, y2) , a félkör
alakú meridiánnal alkotott Q
metszéspontjához vezető r rádiuszvektor - mely a fokhálózat
szögtartásból adódó merőlegessége miatt merőleges az OQ rádiuszvektorra - az y tengelyre leképeződő középmeridiánnal g szöget zár be, a merőleges szárú szögek miatt
tehát az OQ rádiuszvektornak az x tengellyel bezárt szöge ugyancsak g . Az OC2Q derékszögű háromszögből
és
.
A
parallelkörök egyenlete a síkon ezek alapján:
A j szélességi kör és a l hosszúsági kör P metszéspontját a két egyenletből álló
egyenletrendszer megoldása adja. Végezzük el a négyzetre emeléseket:
(Felhasználtuk
a
azonosságot.)
Vonjuk
ki a második egyenletet az elsőből:
,
tehát
Helyettesítsük
be ezt a parallelkör egyenletébe:
Átrendezve:
A
másodfokú egyenletet megoldjuk:
Pozitív l-hoz pozitív x–et
szeretnénk kapni, viszont a sin(k@l) szorzója csak akkor lehet pozitív, ha a
számlálóban a pozitív előjelet vesszük figyelembe. Elvégezve még a nevező
átalakítását:
Helyettesítsük
ezt a meridián és a parallelkör egyenletének különbségébe:
vagyis
Szükségünk
van még a g(j) szögre. Ezt a szögtartás alapegyenletéből
kapjuk meg, mely a komplex függvények elméletéből ismert Cauchy-Riemann differenciálegyenleteknek felel meg.
Írjuk fel ehhez az x és y vetületi egyenleteket a szokásostól eltérően
a izometrikus szélesség és a l földrajzi hosszúság függvényében
(ahol a Y izometrikus szélességet gömb alapfelület esetén a
egyenlőség
definiálja). Eszerint az
és
függvényeknek
szögtartó vetület esetén eleget kell tenniük a
és
differenciálegyenleteknek.
Írjuk fel a parciális deriváltakat Lagrange vetületére:
Mindkét
differenciálegyenletbe elvégezve a behelyettesítést, ugyanazt a
egyenletet
kapjuk. Átrendezés után:
Elvégezve
az integrálást:
.
Felhasználva
az izometrikus szélesség definícióját:
Itt
a d integrációs konstans zérus, mivel az
egyenlítőn (j = 0) g = 0 a ??? ábra szerint. Folytatva az egyenlet
átalakítását:
Ebből
következik
,
végül
A
hossz- és területtorzulási modulusok a vetületi kezdőponttól minden irányba
távolodva nőnek. A világtérkép kontúrvonala mentén e torzulások azonos
nagyságúak.
Ezt
a vetületet a k=0.5 esetre, amely a Földet kör kontúrban ábrázolja,
Lambert német matematikus és térképész alkotta meg 1772-ben. Tetszőleges k-ra Lagrange francia
matematikus általánosította 1779-ben.
Megjegyzendő,
hogy k =1 esetén g =j , ami éppen a transzverzális sztereografikus
vetületet szolgáltatja.
Mind
a parallelkörök, mind a meridiánok képe körív. A Föld kör kontúrban jelenik
meg. Az egyenlítő hossztartó, így a kontúrkör sugara p. Az egyenlítő hossztartásából adódik továbbá a
meridiánok képének középpontja és sugara (ld. ??? ábra).
Jelölje
P a (j,l) koordinátájú pont
képét. rm-mel jelölve a l meridián-körív póluspontjához vezető
rádiuszvektor hosszát, x-vel az x tengellyel bezárt szögét, a körív
C1 középpontjának az origótól mért x1 távolsága az ábráról leolvashatóan:
és
(itt
felhasználtuk az ugyanakkora körívhez tartozó középponti és kerületi szög
közötti összefüggést), továbbá
.
Jelölje r a j parallelkör képének sugarát, y2 a C2 középpont
y koordinátáját. Legyen a j parallelkör és a középmeridián
metszéspontjának t távolsága az origótól az
alábbi egyenlettel megadva:
.
Adja
meg a j parallelkör
r sugarát az alábbi képlet:
.
s-val jelölve a j parallelkör képének C2 középpontját a l meridián képének C1 középpontjával összekötő egyenes és a
középmeridián által bezárt szöget, és figyelembe véve, hogy
,
a
??? ábráról látszik, hogy
.
A l meridián és a
j parallelkör által bezárt q szögre
.
A r hosszúságú rádiuszvektornak a
középmeridiánnal bezárt g szögét adja meg a
képlet.
Innen következik:
A
P ponthoz vezető, rm
hosszúságú rádiuszvektornak az x
engellyel bezárt z szögét adja meg
.
Innen
megkapható z :
.
Végül
a vetületi egyenletek:
és
A
fokhálózat menti hossztorzulások:
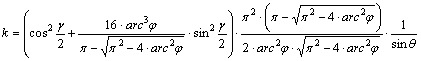
Ezekből
adódóan a vetület általános torzulású.
Az
egyenlítő környékén a torzulások előnyösek, azonban a pólus felé közeledve a
területtorzulások rohamosan nőnek. Ezért előfordul, hogy a sarkok környékét
egyszerűen levágják. (Kisebb mértékben ugyan, de a szögtorzulások is nőnek, ami
a fokhálózati metszési szögeknek a derékszögtől való egyre nagyobb eltérésében
is megnyilvánul, főként a határoló meridiánok környékén.)
A
vetület Alphons J. van der Grinten
amerikai térképésztől származik, aki az 1898-ban publikált vetületet 1904-ben
az Egyesült Államokban szabadalmaztatta. Főleg amerikai világtérképeken fordul
elő, de az utóbbi időben Ny-európai, sőt magyarországi atlaszokban is
előfordul.
Nem
keverendő össze Grinten
II. vetületével, amely szintén kör kontúrban, de ortogonális fokhálózattal jeleníti
meg a Földet.