KÉPZETES VETÜLETEK

A képzetes vetületeket a valódi vetületek tulajdonságai alapján határozzuk meg. Ismeretes, hogy egy vetületet akkor nevezünk valódinak, ha a (segéd-) fokhálózat képe rendelkezik az alábbi tulajdonságokkal:

- a (segéd-) meridiánok képei vagy párhuzamos egyenesek, vagy egy ponton áthaladó egyenesek;

- a (segéd-) parallelkörök képei vagy párhuzamos egyenesek, vagy koncentrikus körök vagy körívek;

- a (segéd-) fokhálózati vonalak derékszögben metszik egymást.

Képzetesnek ezek után azokat a vetületeket nevezzük, amelyeknek (segéd-) fokhálózatára a fentiekben felsorolt három ismérv közül legalább az egyik nem teljesül.

Természetesen a fenti tulajdonságok közül egyik-másik a képzetes vetületekre is fennállhat, és ezek osztályozása éppen az ilyen tulajdonságokon alapul. Nevezetesen az ún. képzetes síkvetületeknél a (segéd-) parallelkörök képei koncentrikus körök, de a (segéd-) meridiánok képei nem egy ponton áthaladó egyenesek. Az ún. képzetes hengervetületeknél a (segéd-) parallelkörök képei ugyan párhuzamos egyenesek, de a (segéd-) meridiánok képei nem lehetnek párhuzamosak. Az ún. képzetes kúpvetületeknél a (segéd-) parallelkörök képei - nem feltétlenül koncentrikus - körívek, de a (segéd-) meridiánok képei nem lehetnek egy pont felé összefutó egyenesek; viszont a (segéd-) fokhálózat merőlegessége nem kizárt. Végül az ún. egyéb képzetes vetületeknél sem a (segéd-) meridiánok, sem a (segéd-) parallelkörök képei - a fokhálózat esetleges merőlegessége kivételével - nem rendelkeznek a fenti tulajdonságokkal.

A képzetes vetületek torzulási szempontból bonyolultabbak a valódi vetületeknél. Minthogy a fokhálózati vonalak által bezárt q szög a képzetes vetületek nagy részénél csak a térkép kitüntetett pontjain vagy vonalain (pl. a középmeridián mentén) derékszög, ezeknél a vetületi főirányok általában nem esnek egybe a fokhálózat irányaival. A torzulási ellipszis adatainak megismeréséhez tehát a fokhálózat menti hossztorzulásokon kívül szükségünk van a q meghatározására is.

Képzetes síkvetületek

A (segéd-) parallelkörök képei koncentrikus körök, a (segéd-) meridiánok képei tetszőleges törvényszerűséget követő görbe vonalak. A (segéd-) meridiánok és a (segéd-) parallelkörök a tengelyeken kívül általában nem metszik egymást merőlegesen, emiatt a képzetes síkvetületek között nincsen szögtartó.

A valódi síkvetületekhez hasonlóan a koordinátarendszer origója a pólus képébe kerül, az y tengely a középmeridián képére esik, amely egyben a fokhálózat szimmetriatengelye, és a j szélesség helyett a b=90°-j pólustávolsággal dolgozunk. A vetületi egyenletekhez célszerű a polárkoordinátás alakot használni, ahol r=r(b) a sugárfüggvény, g=g(b,l) pedig a b,l földrajzi koordinátákkal adott pont képéhez vezető rádiuszvektornak az y tengely negatív felével bezárt szöge. A r=r(b) a b-nak, g=g(b,l) pedig l-nak szigorúan monoton növő függvénye, és limg(b,l)=0 l®0 esetén. Egy adott b,l koordinátájú pont térképi síkkoordinátáit ekkor az

képletekkel adhatjuk meg (ld. ??? ábra). A szimmetria miatt az x=x(b,l) vetületi egyenlet l-ban páratlan, y=y(b,l) pedig l-ban páros.

A fokhálózat menti torzulások a következő alakban írhatók fel:

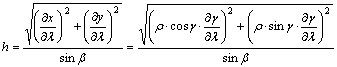
A kiemelések elvégzése után tehát:

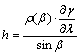
Továbbá

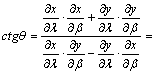
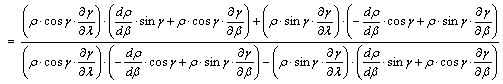
Egyszerűsítve a kifejezéssel és elvégezve az összevonásokat kapjuk, hogy

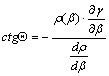
Innen

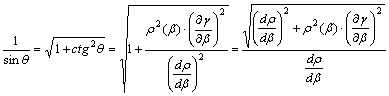
A k meridián menti hossztorzulás:

Ezt bővítve dr/db-val és felhasználva az előző egyenlőséget kapjuk, hogy

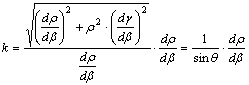
A területtorzulási modulus:

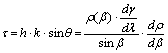
E vetülettípus alapgondolata Ginzburg orosz kartográfustól ered (1952), aki a r sugárfüggvényre a következő alternatív képleteket javasolta:

(középmeridiánban hossztartó), vagy

;

A g szög általános alakja:

;

a gyakorlatban a

képlet használatos (b_H az ábrázolandó területet határoló parallelkör pólustávolsága).

A k együttható lehetséges értékei 1 vagy 2; k=1 esetén a fokhálózatnak csak egy szimmetriatengelye van: a 0° és a 180° meridián képe. k=2 esetén ezeken kívül a ±90° meridián képe is szimmetriatengely lesz.

A c és q együttható a meridiánok görbültségét határozzák meg. c javasolt értéke 0.002 és 0.2 közé esik; minél nagyobb, annál görbültebb a meridiánok képe. A q együttható értéke a meridián görbültségének változását befolyásolja; választható értékei: q=1 vagy q=2.

A maximális szögtorzulás izovonalai a képzetes síkvetületben ovális alakúak, ezért elsősorban ovális alakú terület megjelenítésére ajánlhatók. Ha a

képletet használjuk, akkor az ovális alakzat nagytengelye a középmeridián irányába mutat. Ha erre merőlegesnek akarjuk választani a nagytengely irányát, akkor a

alak érvényes.

A kétszeresen szimmetrikus (k=2) képzetes síkvetület fokhálózatát

transzverzális és ferdetengelyű elhelyezésben a következő ábrák mutatják.

A fentiekben leírt képzetes síkvetület alkalmazását Ginzburg akkor ajánlja, ha kívánatos a Föld gömb-alakjának érzékeltetése, vagy ha az ábrázolandó terület ovális alakú. Ezért javasolható pl. az Atlanti óceán alkalmazására. Oroszország európai területének ábrázolására is előszeretettel használják.