Lecture notes – Chapter 1

The draft of the cartographical representation of the Earth surface

In the cartography a three-dimensional figure – the Earth’s surface with its objects – will be represented in two-dimensional space – on the plane (on paper or on a screen). To the localization of the points of these objects to be represented, their coordinates must be known either on the Earth’s surface, or on the plane. The connection between the coordinates of two kinds – a mapping („map projection”)– comes true by the so called „projection equations”.

Expected properties for the two surfaces:

- continuous

- regular

- describable by formulae or series

Expected properties for the mapping between the two surfaces:

- twice continuously differentiable

- injective

- describable by formulae or series

Substitution of the physical Earth’s surface by an approximate one, satisfying the conditions

The Earth’s irregular surface as geographical relief (with elevation) will be projected onto the geoid, disregarding the elevation

Geoid:

- let the gravitational equipotential surfaces (where magnitude of force of gravity is the same) be considered; the direction of the gravitational vector, the „local vertical” traced out by the plumb line is everywhere perpendicular to these surfaces

- chosen one from these surfaces, which coincides the mean sea level supposed being at rest, and extended it to the area of continents in imagination

- it is irregular surface, too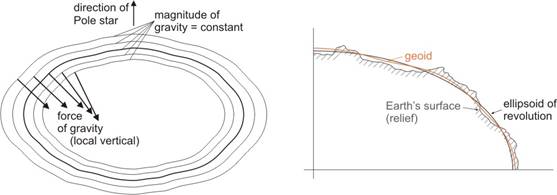

The representation of the Earth’s surface and its objects, projected onto the geoid needs a regular, describable by formulas (or series) and continuous approximating geometrical shape. Options, depending on the accuracy of the representation (with its well-known equation in the spatial rectangular coordinate system):

Plane (area  < 10 km²)                                  

Sphere (scale of mapping < ~ 1 : 1 million)          

Ellipsoid of revolution (spheroid) – hereafter ellipsoid (a surface of revolution obtained by rotating an ellipse about its shorter axis)

Sketch of the representation of the globe surface on maps:

1. abstraction step:                        2. abstraction step:                        mapping („map projection”):

Earth’s surface ® geoid geoid ® ellipsoid (or sphere)     ellipsoid (or sphere)    ® plane

(irregular)           (irregular)           (irregular)                   (regular)     (regular)                             (regular)