Lecture notes – Chapter 2

Main properties of an ellipsoid of revolution

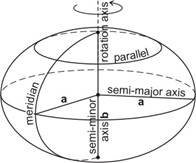
a – semi-major axis, radius of the Equator

b - semi-minor axis

f – flattening or 1/f – inverse flattening

e – first eccentricity (there is often used its square e², too)

e’ – second eccentricity and its sqare (e’)²

Generally a and 1/f are given; then e² and b can be calculated:

and

For example WGS’84 ellipsoid:

a = 6 378 137.0 m

1/f = 298.257 223 563

e² = 0.006 694 379 990 14

e = 0.081 819 190 9

b = 6 356 752.31 m

e’ = 0.082 094 438 06

Other ellipsoids in use: e.g., Bessel, Clarke 1880, Hayford, etc.

Coordinate systems on the surface of sphere and ellipsoid of revolution

Coordinate system on the spherical surface:

Let a spatial polar coordinate system be considered, whose origin is in the centre O of the sphere, and its polar axis coincides with a rotation axis of the sphere, which corresponds to the Earth’s rotation axis.

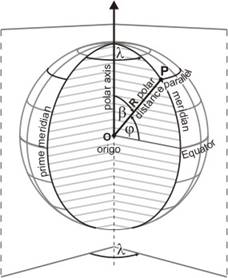
Coordinates of the point P:

r is the polar distance (which equals the radius R of the sphere, a constant value), it can be neglected

angle b is the polar angle;

angle j (the complementary angle of b, that is j=90°– b) is the „geographical latitude”; its sign is positive on the northern hemisphere

angle l is the angle of two semi-planes, containing the rotation axis, one of the semi-planes is the fixed prime semi-plane, the other contains the point P; this azimuthal polar angle is the „geographical longitude”, its sign is positive on the eastern hemisphere

The latitude j and the longitude l are considered as the geographical coordinates on the spherical Earth.

Coordinate lines of the geographical coordinates can be obtained by fixing one of the coordinates, while the other varies. They construct the graticule:

j is fixed: „parallel” („circle of latitude)”; -90°£j£90°, j=±90° „North and South Pole”; j=0° Equator

l is fixed: „meridian” („circle of longitude)”; -180°£j£180°, l=0° prime meridian; l=±180° „Date Line”

Geometric dimensions of the graticule lines on the sphere with radius R:

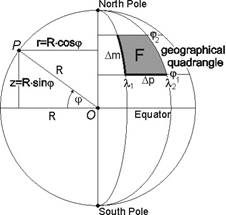
The radius r of the parallel of latitude j:

Length Dp of the parallel arc with latitude j between the meridians l₁ and l₂:

(Henceforth, arcd will denote the arc measure of the angle d° given in degree measure, and

The distance z of the parallel of latitude j from the Equator:

Length Dm of an arbitrary meridian arc between the parallels of latitudes j₁ and j₂:

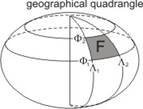
The surface area F_F of a spherical zone between the equator and the parallel of latitude F is:

The surface area F of geographical quadrangle buonded by the parallels of latitudes j₁ and j₂ , as well as the meridians of longitudes l₁ and l₂:

Coordinate system on ellipsoidal surface

Latitudes on the ellipsoid of revolution

1. Similarly to the sphere, let a spatial polar coordinate system be considered, whose origin is in the centre of the ellipsoid, and its polar axis coincides with the ellipsoid’s rotation axis, corresponding the Earth rotation axis.

The angle Y (=90°– b) is the „geocentric latitude”, where b is the polar angle;

2. Let the ellipsoid be transformed into a sphere of radius a by an affinity with a ratio of a/b to the direction of the rotation axis, and let the spherical polar coordinates be taken on this sphere of radius a. Then j (=90°– b) is the „reduced (or parametric) latitude”, where b is the polar angle on the transformed sphere. The polar distance r equals always a, so it can be neglected.

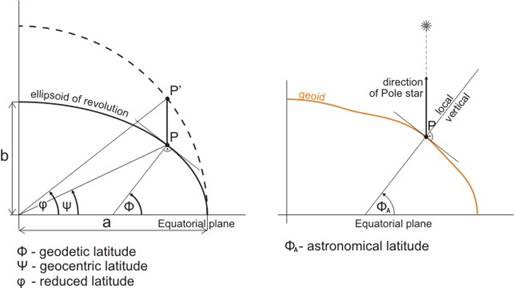
3. The „geodetic latitude” F is the angle between the equatorial plane and the direction perpendicular to the ellipsoidal surface (that is perpendicular to the tangent plane of the surface) at the point P.

This latitude can be measured approximately with the help of the angle between the local perpendicular of the geoid (plumb) and the plane, perpendicular to the direction towards the Pole-star („astronomical latitude”).

Longitude on the ellipsoid

Longitude L on the ellipsoid can be interpreted on the same way, as l on the sphere – by the azimuthal polar angle. The longitude difference on the physical Eart’s surface can be measured by astronomical tools, with the help of the time difference of the culmination on the whereabouts. 1 hour time difference corresponds to 15° longitude difference.

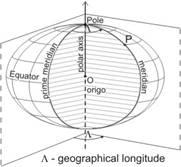
The F geodetic latitude and the L ellipsoidal longitude together are regarded as the geographical coordinates on the ellipsoid of Earth.

The coordinate lines on the ellipsoid by fixing one of the coordinates construct the graticule.

F is fixed: „parallel (circle of latitude)” (its sign is positive on the northern hemisphere); -90°£F£90°, F=±90° „North and South Pole”; F=0° Equator

L is fixed: „meridian (line of longitude)” (its sign is positive on the eastern hemisphere); -90°£L£90°, L=0° prime meridian; L=±180° „Date Line”.

Two meridians with a longitude difference of 180° create a bimeridian both on the sphere and the ellipsoid, which is a plane curve, of course.

The prime meridian is appointed by the prime semi-plane of the coordinate system globally or locally, in connection with the spreading of the area to be surveyed and/or represented. The Greenwich prime meridian has been used in the satellite navigation, the international orientation systems and topographic map systems, as well as in the geocartography (small-scale maps). The Ferro prime meridian (El Hierro, Canary Island) 17° 40’ west of Greenwich was current earlier, mainly in Europe. Some countries in eastern Europe use the Pulkovo prime meridian (St Petersburg, Russia) 30° 20’ east of Greenwich.

E.g., the Gellérthegy prime meridian is in use on the topographic maps in Hungary (Bessel-ellipsoid, datums HD1863, HD1909: 36°42'51.69" east of Ferro; IUGG’67 ellipsoid, datum HD72: 19°2'54.856" east of Greenwich).

Geometric dimensions of graticule lines on the ellipsoid with semi-axes a and b:

The parallels of the ellipsoid

The equation of a bimeridian curve with its centre in the origin in the r,z planar coordinate system:

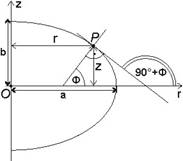
Let us express z as function of r whose graph coincide the upper part of the ellipse:

and its derivative is

On the other hand, the derivative means the slope of the tangent line, whose angle with the axis r is equal (90°+F) at a point P on the parallel F. So,

The consequence of the two equalities concerning :

After squaring of this equation, the coordinate r can be expressed, which is the radius of the parallel of latitude F:

Substituting r into the equation of the ellipse, z² can be expressed:

So,

Connections between the several latitudes on the ellipsoid

On the basis of figure above:

Transforming the ellipsoid by affinity with the ratio of a/b into a sphere of radius a, the position vector of the point P – the arm of the geocentric latitude – passes into the arm of the reduced latitude, that is

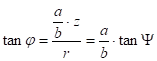
It follows from these

As and , the relation among the three latitudes:

N: the radius of curvature normal to the meridian

Definition of an osculating circle: a circle, passing through the point P of a sufficiently smooth plane curve, considered as the graph of a twice differentiable function, whose first and second derivatives equal the first and second derivatives of the curve. Its radius is called radius of curvature. (Considering a circle, in its every point the osculating circle coincides with the circle itself.)

Let an ellipsoidal surface be sectioned by an arbitrary plane, passing through the surface point P with latitude F. The intersection line’s radius of curvature at P is in the limelight. First of all the normal section – containing the straight line, perpendicular to the surface – plays a significant role. Its plane and the tangent plane intersect each other in a single straight line, crossing the point P. Skew sections can be obtained by rotating the plane of the normal section about this intersection line. According to Meusnier’s theorem, the ratio at the point P which comes into existence between the radius of curvature of any such skew sections containing the intersection line on the one hand, and the radius of curvature of the normal section on the other, is equal to the cosine of the angle d between the section’s planes. (It means that if all sections containing a common tangent line at a point P of a smooth surface are taken, the normal section has the longest radius of curvature at P out of them.)

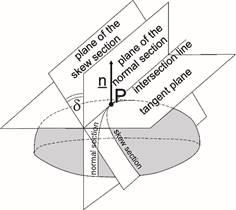
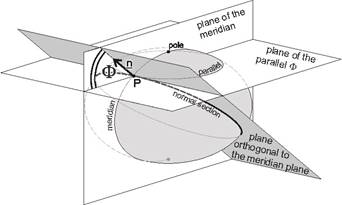
Let the plane of the meridian containing the point P, moreover the orthogonal plane containing both P and the normal vector n perpendicular to the meridian be taken (see figure above). Let the radius of curvature of this latter normal section at P be denoted by N. The plane of the parallel F containing P is orthogonal, too. So the angle of two orthogonal planes is equal to F, then from the Meusnier’s theorem follows

N depends only on the latitude F because of the rotation symmetry of our ellipsoid, so

N is called the radius of curvature normal to the meridian (or prime vertical radius of curvature). With its help the formula of r is:

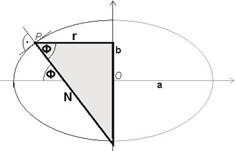
The figure above is showing that the distance between the point P and the rotation axis along the straight line perpendicular to the meridian line at P is the length of the hypotenuse in a right triangle with leg r and acute angle F, thus it can be got from the formula

on the one hand, and this quantity provides exactly N(F) on the other.

N(F) can be inserted into the formula of z:

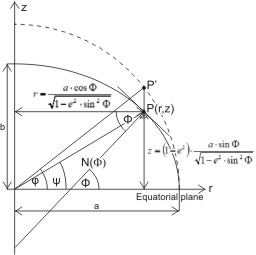
The meridians of the ellipsoid. M: meridian radius of curvature

The meridian line belonging to the longitude L is a semi-ellipse with semi-axes a and b.

Let the radius r of osculating circle of this ellipse be considered at the point P₀ with coordinates (r₀,z₀) depending on its latitude F₀.

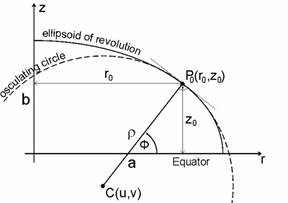
The well known formula of the meridian arc as a function:

, where r=r(F)

The formula of the osculating circle with (temporarily unknown) radius r and coordinates of the centre point C(u,v):

The above definition of the osculating circle lead up to the next three equations:

(The point P₀ with coordinates r₀,z₀ is the common point of the two figures.)

(The two figures at the point P₀ with coordinates r₀,z₀ has a common tangent.)

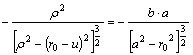
(The second derivatives are equal at the point P₀ with coordinates r₀,z₀ .)

The solution of this system of equations results in the radius r of the osculating circle at the point P of latitude F₀:

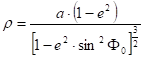
Its name is meridian radius of curvature, and denoted by M. It varies depending on the latitude F:

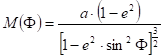
Because of the flattening of the ellipsoid, this radius is shortest on the Equator, and longest at the Pole.

Calculation of length along the graticule of the ellipsoid

Length Dp of the parallel arc with latitude F between the meridians L₁ and L₂:

Length Dm of the meridian arc between the parallels F₁ and F₂:

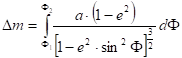
which can be calculated numerically (e.g. by trapezoidal or Simpson’s rule).

The distance Dz between the plane of the parallels with latitude F₁ and F₂:

The surface area F_F of an ellipsoidal zone between the equator and the parallel of latitude F is:

Consequently, the surface area F of the geographical quadrangle buonded by the parallels F₁ and F₂, as well as the meridians L₁ and L₂: