Lineáris egyenletrendszerek megoldásának egy módszere

A térképészet és a geodézia számos problémája igényli lineáris egyenletrendszer megoldását.

Ilyen feladat adódik többek között akkor, amikor egy bizonyos vetületű térkép egy pontjának síkkoordinátáit át akarjuk számítani egy másik vetület síkkoordinátáiba. Ez végrehajtható pl. polinomos átszámítási transzformációval, ahol a második vetületbeni X₂,Y₂ koordináták közelítő értékeit sorra az első vetületbeni X₁,Y₁ koordináták polinomjából számítjuk. Másodfokú polinom alkalmazása esetén:

A transzformációs polinomok A_i és B_i együtthatóinak meghatározásához szükség van olyan illesztőpontokra (esetünkben 6-ra), amelyeknek mindkét vetületben ismerjük a koordinátáit. Az illesztőpontok koordinátáit sorra behelyettesítve a fenti egyenletekbe, két lineáris egyenletrendszert kapunk (esetünkben egy-egy 6 ismeretlenes, 6 egyenletből álló lineáris egyenletrendszert az A_i-kre és a B_i-kre). Az egyenletrendszerek megoldásából kapott A_i és B_i együtthatók birtokában tetszőleges első vetületbeni X₁,Y₁ koordinátákból közelítőleg kiszámíthatjuk a második vetületbeni X₂,Y₂ koordinátákat.

Hasonlóan lineáris egyenletre vezet az a feladat, amelynél az illesztőpontok száma nagyobb az előre rögzített fokszámú transzformációs polinomok együtthatóinak számánál. Ebben az esetben a pontok második vetületbeli koordinátáinak becsült és pontos értékei közti különbségek négyzetösszegének minimalizálása adja a megoldandó lineáris egyenletrendszert.

Tekintsük az x₁, x₂, x₃, … x_n ismeretleneket tartalmazó, n egyenletből álló lineáris egyenletrendszert:

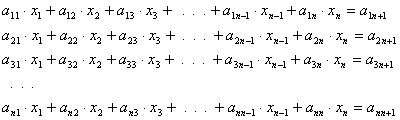
Ez az egyenletrendszer egyértelműen megoldható, ha az egyenletek baloldalán álló a_ij együtthatókból öszeállított D determináns nem zérus:

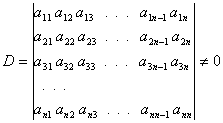
A megoldás ekkor megkapható pl. az ismert Cramer-szabály segítségével.

Bizonyos speciális esetekben a lineáris egyenletrendszer egyszerűen megoldható. Vegyük pl. azt az esetet, amikor az együtthatókból összeállított mátrix főátlója alatt csupa 0 elem áll, és a főátlóban nincs 0 elem („felső háromszög alakú” együtthatómátrix). Ekkor az egyenletrendszerünk:

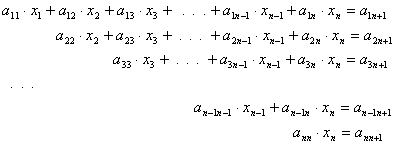
A legalsó egyenletből megkapható x_n. Ezt behelyettesítve a felette lévő egyenletbe, abból ki lehet számítani x_n-1 -et. Alulról felfelé haladva így az összes ismeretlen meghatározható.

A Gausstól származó kiküszöböléses eljárás célja az, hogy az egyenletrendszert ekvivalens átalakításokkal a fenti alakra hozza. Ilyen, az egyenletrendszer gyökeit nem befolyásoló átalakítás pl. valamely egyenletnek egy 0-tól különböző számmal való végigszorzása vagy végigosztása, továbbá valamely egyenlet konstans-szorosának egy másik egyenlethez való hozzáadása vagy abból való levonása.

Induljunk ki ehhez az

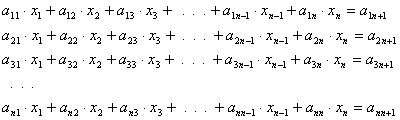
egyenletrendszerből. Ha a₁₁¹0, akkor az első egyenletet osszuk végig a₁₁-gyel:

ahol a_1j* a leosztás után kapott együttható.

Most ennek az egyenletnek a konstans-szorosait fogjuk levonni a többi egyenletből, éspedig az i-edik egyenletből levonjuk az első egyenlet a_i1-szeresét, aminek eredményeként az i-edik egyenlet első ismeretlenének együtthatója zérussá válik. Ezt végrehajtva az összes többi egyenletre, az egyenletrendszerünk az alábbi lesz:

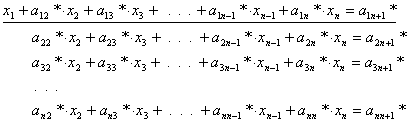
ahol a_ij* (i=2,3,…,n; j=2,3,…,n+1) a műveletek végrehajtása után kapott együttható. Ilyen módon az egyenletrendszerünk első egyenletével „elimináltuk” (kiküszöböltük) az első ismeretlent a többi egyenletből.

Az első egyenletet a továbbiak során figyelmen kívül hagyva, marad egy n-1 ismeretlenes, n-1 egyenletből álló egyenletrendszerünk. Ha a₂₂*¹0, akkor ennek legfelső egyenletét végigosztjuk a₂₂*-gal:

ahol a_2j** a leosztás után kapott együttható.

Ennek az egyenletnek az a_i2*-szorosát levonjuk az i-edik egyenletből (i=3,…,n), amivel kiküszöböltük az szóbanforgó egyenlet alatti egyenletekből a második ismeretlent:

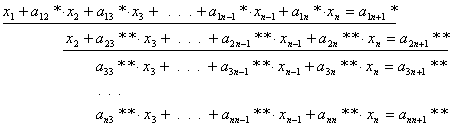
ahol a_ij** (i=3,…,n; j=3,…,n+1) a műveletek végrehajtása után kapott együttható.

Az eljárást a két első egyenlet figyelmen kívül hagyásával folytatva, a megmaradt n-2 ismeretlenes egyenletből álló n-2 ismeretlenes egyenletrendszerből a legfelső segítségével kiküszöböljük a harmadik ismeretlent. Ezt ismételgetjük ciklikusan oly módon, hogy az l-edik eliminációs ciklusban az l-edik egyenlet segítségével kiküszöböljük az alatta lévő egyenletekből az l-edik ismeretlent. A kiküszöbölés során az a_ij*^…*×x_j tagok

-vé változnak (i=l+1,…,n, j=l+1,…,n). Ezt az eljárást l=n–1 -ig folytatjuk, aminek eredményeként az egyenletrendszerünk együtthatómátrixa felső háromszög alakúvá válik, és az ott leírt módon megoldható. Az itt leírt eljárást szokás Gauss-eliminációnak nevezni.

Ha a kiindulási D¹0 feltétel nem teljesül, akkor az azt jelenti, hogy az egyenletrendszerünknek vagy nincs megoldása, vagy végtelen sok megoldása van. Abban az esetben, ha a kiküszöböléses megoldás végrehajtása során az egyik egyenlet baloldalán minden együttható zérussá válik, de a jobboldalon nullától különböző szám áll, akkor az egyenletrendszerünknek nincs megoldása. Ha viszont egy egyenlet azonossággá válik (pl. úgy, hogy a baloldalon valamennyi együttható zérus, és a jobboldalon is nulla áll), akkor az egyenletrendszernek végtelen sok megoldása van.

A fentiekben leírt műveletek közül az a_ll*^…*-lel való osztás csak akkor hajtható végre, ha a_ll*^…*¹0. Ellenkező esetben az l-edik ismeretlen eliminálandó együtthatói közül érdemes kiválasztani a legnagyobb abszolút értékűt, és ennek sorát az l-edik sorral kicserélni, ami után az eljárás folytatható – ez az ún. részleges főelemkiválasztás. (Itt felhasználtuk azt, hogy az egyenletek sorrendje nem befolyásolja az egyenletrendszer gyökeit.)

Az a_ll*^…*-lel való osztás akkor is pontatlan gyököket eredményezhet, ha ugyan a_ll*^…*¹0, de kicsi abszolút értékű szám. A Gauss-eliminációt ezért célszerű kiegészíteni az ún. teljes főelem-kiválasztással. Ennek lényege, hogy az osztásokat mindig a legnagyobb abszolút értékű együtthatóval végezzük. Tehát az l-edik eliminációs ciklusban az eljárásban részt vevő együtthatók közül kiválasztjuk a legnagyobb abszolút értékű a_ij*^…* együtthatót, majd az ennek sorában álló egyenletet (az i-edik sort) kicseréljük az l-edik sorban álló egyenlettel, a j-edik ismeretlen oszlopát pedig az l-edik ismeretlen oszlopával. (Az alábbi egyenletrendszerben aláhúztuk azt a két felcserélendő tagot, amelyek sorát és oszlopát fel kell cserélni.)

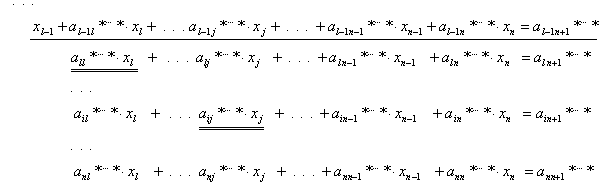
A sorcsere, mint láttuk, nem befolyásolja az egyenletrendszer gyökeit, azonban az oszlopcsere megváltoztatja a gyökök sorrendjét. Az eljárás végén megkapott gyököket ezért páronként vissza kell cserélgetni, éspedig az oszlopcserék végrehajtásával ellentétes sorrendben.