Számítási módszerek a térképészetben

 

 

Nem-lineáris egyenletek gyökének meghatározása

 

Nem-lineáris egyenletekkel gyakran találkozhatunk a térképészeti és a geodéziai számítások során. Egy ilyen egyenlet általánosságban

           

alakú, ahol  h1(x) és h2(x)  nem-lineáris függvények. Az egyenlet megoldása olyan   gyök meghatározását jelenti, amelyet az egyenletbe helyettesítve, az egyenlőség teljesül:

           

Grafikusan az    gyök a közös koordinátarendszerben ábrázolt

           

és az

           

függvények grafikonja metszéspontjának  x  koordinátájaként állítható elő (???ábra).

 

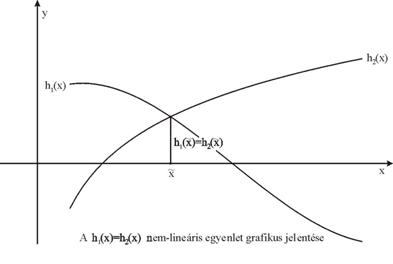
Célunk az egyenlet gyökének kívánt pontosságú numerikus előállítása.

 

Tekintsünk egy példát a nem-lineáris egyenletre. Ismert, hogy a forgási ellipszoidról gömbre történő szögtartó leképezésben (az ún. szögtartó gömbvetületben) az  ellipszoidi  F,L  és a gömbi  j, l  koordináták között az alábbi egyenletek adják meg az összefüggést:

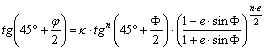
és

           

A szélességekre vonatkozó egyenletből a  j  gömbi szélesség kifejezhető:

             ,

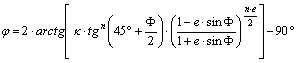a  F  ellipszoidi szélesség azonban nem írható fel explicit alakban a  j  gömbi szélesség függvényében. Ha adott  j -ből  kell  F-t kiszámítanunk, akkor a geodéziai szakirodalom az egyenlet átrendezését ajánlja:

             ,

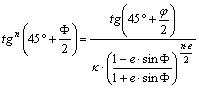majd a baloldali képletből a  F  kifejezését:

             .

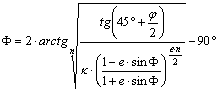Rögzített  j  gömbi szélesség mellett – a jobb oldali kifejezésbe a  F  ellipszoidi szélesség egy közelítését behelyettesítve – ez a képlet a  F  javított értékét eredményezi. Ezt az eljárást többször megismételve, az ellipszoidi szélesség egyre pontosabb közelítéseit kapjuk. Felmerül a kérdés, hogy mi biztosítja a fenti eljárás konvergenciáját (azaz hogy valóban egyre pontosabb és pontosabb közelítéseket kapunk), továbbá hogy más átrendezés esetén mikor várható hasonló eredmény.

 

Példa-egyenletünk bármely alakjában a  F  ismeretlen helyére  x-et írva és  j -t konstansnak tekintve, visszatérhetünk a bevezetőben alkalmazott jelölésre. A legutóbbi alaknál pl.:

             ,

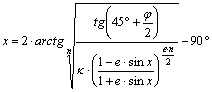vagyis ebben a

           

alakú egyenletben

           

és

           

 

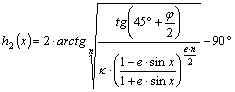
Visszatérve az általános alakhoz, a továbbiakban a

           

egyenletet rendezzük  0-ra:

           

A kiindulási egyenletünk megoldását tehát az  f(x)  nem-lineáris függvény    zérushelyének meghatározására vezetjük vissza (???ábra).

 

 

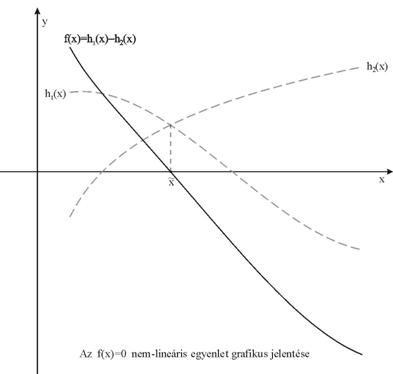
Az

           

egyenlet közelítő megoldására több módszer ismeretes. Ezek közül tekintünk át néhányat az alábbiakban.

 

 

A fokozatos közelítések módszere

 

Alakítsuk át az

egyenletet oly módon, hogy kifejezzük az egyenletből az  x  ismeretlent, ami többnyire megtehető. Az átalakított egyenletünk ekkor az alábbi alakú:

           

ahol  g(x)  6nem-lineáris függvény. Képezzük ennek segítségével az  xi  sorozatot az

           

képlet alapján. Ha ez a sorozat konvergens, akkor az  -mal jelölt  határértéke lesz az egyenlet gyöke, vagyis

           

 

 

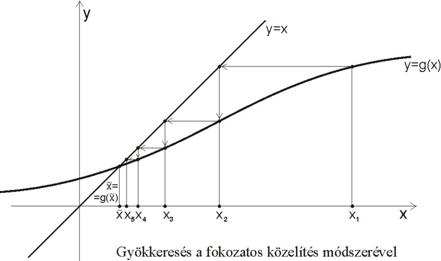
A konvergenciához elégséges feltételre van szükségünk. Tegyük fel, hogy az egyenletünk jobb oldalán álló  g(x)  függvény  x1  és    között differenciálható, és

           

Ekkor  –  felhasználva a Lagrange féle középértéktételt:

             ,

ahol  u  az  xi  és    közé esik. Hasonlóan látható, hogy

             .

Az eljárást  -ig folytatva, teljes indukcióval látható, hogy

             .

K<1  miatt  Ki®0,  és ez a jobboldali kifejezés 0-hoz tartása miatt biztosítja a konvergenciát, vagyis:               

.

Adjunk meg még egy korlátot az    hibához a fenti elégséges feltétel fennállása esetére.

Induljunk ki ehhez a háromszög-egyenlőtlenségből:

           

A Lagrange-középértéktétel fenti következményéből adódik, hogy

           

A két egyenlőtlenség együttes alkalmazásából átrendezéssel következik, hogy

           

Kiemelés és átszorzás után:

           

Eszerint ha két egymást követő közelítés eltérése kicsi, akkor a közelítésünknek a gyöktől való eltérése is kicsi.

 

A fokozatos közelítések módszere nem mindig előnyös, mert egyrészt bonyolultabb egyenletek esetén  x  kifejezése az egyenletből hosszabb számolást igényelhet, másrészt a konvergencia elégséges feltételének biztosítása, illetve fennállásának ellenőrzése sem mindig egyszerű. A továbbiakban egyszerűbb módszert igyekszünk találni.

 

Gyökkeresés az intervallumfelezés módszerével

 

Ha egy intervallumon értelmezett folytonos  f(x)  függvényhez van olyan  x1  és  x2 pont, melyekben ellenkező előjelű értékeket vesz fel, vagyis

            ,

akkor Bolzano tétele miatt a függvénynek  x1  és  x2  között van    zérushelye, amely gyöke az egyenletünknek:

           

Határozzuk meg az  [x1, x2]  intervallum  x3  felezőpontját:

           

Kivételesen előfordulhat, hogy éppen

            ,

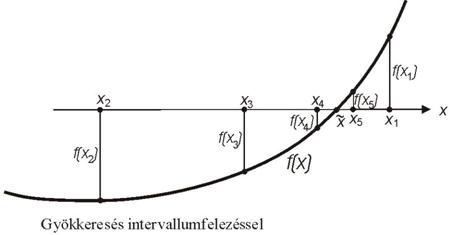
és ezzel találtunk egy gyököt. Amennyiben viszont  f(x3)¹0, akkor vagy  f(x3)>0, vagy  f(x3)<0. A két fél-intervallum közül az egyikben biztosan kell lennie gyöknek, éspedig abban, amelynek végpontjaiban a függvényértékek különböző előjelűek. Ezt tovább felezve kapjuk az  x4  pontot (???ábra), stb.

           

A gyököt biztosan tartalmazó intervallum hossza az  i-edik felezés után:

           

Ez biztosítja az eljárás konvergens voltát. Az eljárást akkor tekinthetjük befejezettnek, ha az i-edik felezés eredményeképpen kapott intervallum hossza a megkívánt pontosságnál kisebb; a gyököt ekkor pl. ezen intervallum felezőpontjával közelíthetjük. Az eljárás azonban nincs tekintettel az  f(x)  függvény menetére, ezért konvergenciája lassú lehet.

 

A húrmódszer

 

Tekintsük ismét az

           

egyenletet, ahol  f(x) folytonos. Az  x1, x2  kezdőértékekre vonatkozólag itt is kikötjük, hogy álljon fenn az

           

egyenlőtlenség. A húrmódszer az intervallumfelezéses módszer javításának tekinthető annyiban, hogy az  f(x)  függvény görbéjének  x1, f(x1)  és  x2, f(x2)  koordinátájú pontjait összekötő egyenes metszi ki az  x  tengelyen az  x3  pontot (???ábra). A két ponton áthaladó egyenes egyenlete:

           

Ez egy lineáris függvény, melynek zérushelyét jelöljük  x3 –mal:

           

Az egyenletből  x3  kifejezhető:

           

Ez után  x1  és  x2  pontok közül azt tartjuk meg, amelyre igaz, hogy

               (i=1,2) ,

a másik pontba  x3  értékét visszahelyettesítve, az eljárást a szükséges pontosság eléréséig ismételgetjük (???ábra).

           

 

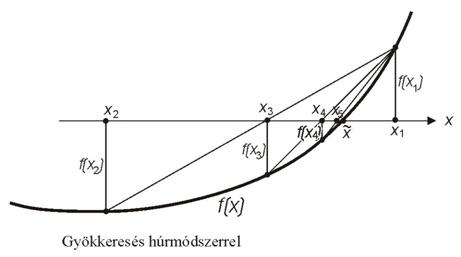
A konvergencia sebessége megfelelő feltételek mellett becsülhető. Ha ugyanis az  [x1, x2]  intervallumon teljesülnek az első és második derivált abszolút értékére az alábbi korlátossági feltételek:

           

(az  f(x) szigorúan monoton), és

            ,

továbbá a

           

jelölés mellett feltesszük, hogy

            ,

akkor

            ,

tehát  i®¥  esetén  xi®.

 

A tétel belátásához vegyük az  f(x)  függvény másodfokú közelítését az  [x1, x2]  intervallumban. Ezt a másodfokú közelítést írjuk fel a lineáris  l(x)  függvény és egy másodfokú  p(x)  függvény összegeként (ahol  l(x)  az  x1, f(x1)  és  x2, f(x2)  koordinátájú pontokon áthaladó egyenes,  p(x)  pedig az  x1, x2 végpontokban  0  értéket felvevő függvény):

           

ahol  v0[x1, x2]. Ekkor az  l(x)  lineáris függvénynek az  -mal jelölt gyökben felvett értéke egyrészt:

            ,

ahol  w0[x1, x2],  másrészt:

           

(Felhasználtuk            itt Lagrange középérték-tétele mellett azt, hogy  l(x3)=0  és  .)

A fenti két egyenletből kapjuk, hogy

           

A feltételek miatt

             ,

amiből adódik, hogy

           

Ehhez hasonlóan látható, hogy

           

(ahol  i=1 vagy 2). Innen következik

           

Ennek analógiájára

           

(ahol  j=i, azaz 1 és 2 közül valamelyik, vagy 3). Innen

           

stb., és ezzel a tételünket beláttuk.

 

A szelőmódszer

 

A húrmódszer kezdőpontjaiban a függvényértékek különböző előjelűeknek kell lenniük. A szelőmódszer a húrmódszer olyan módosítása, amely ezt kikerüli, és csak a kezdőpontokban felvett függvényértékek különbözőségét írja elő, továbbá a húrmódszernél általában gyorsabb konvergenciát biztosít.

 

Messe az  x1, f(x1)  és  x2, f(x2)  koordinátájú pontokat összekötő egyenes az  x  tengelyt az  x3  pontban (???ábra). Ezt – feltéve, hogy  f(x1)¹ f(x2) –  a húrmódszernél megismert képlettel kapjuk meg,:

           

Ez után – tekintet nélkül  f(x3)  előjelére, de kikötve, hogy  f(x2) ¹ f(x3)  –  hasonlóan kapjuk

f(x4) –et. Általánosságban

           

ahol  f(xi-1) ¹ f(xi) (???ábra).

           

 

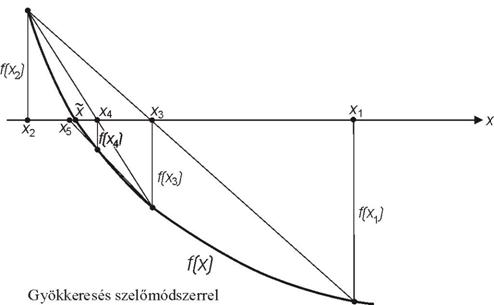
A szelőmódszer tehát – bár a konvergencia nincs mindig garantálva – általánosabb feltételek között alkalmazható, mint a húrmódszer. Emellett ha fennáll a konvergencia, akkor az a húrmódszerénél gyorsabb. Ennek belátásához induljunk ki a húrmódszernél kikötött feltételekből, vagyis    mellett az  [x1, x2]  intervallumon legyen

           

és

            ,

továbbá

            .

 

A kezdőértékre vonatkozó feltételünk miatt  f(x1)¹ f(x2), ezért a fenti képletből kiszámítható x3,  amely megegyezik a húrmódszerből származó értékkel, és a szigorú monotonitás következményeként különbözik mind  x1-től, mind  x2-től. Továbbra is  -mal jelölve a gyököt, a húrmódszernél látottak alapján kapjuk, hogy

           

és

             ,

innen pedig

.

 

f ’(x3)¹0 miatt  f(x3) ¹ f(x2), tehát a fenti képletből  x4  is képezhető. Az előbbiekhez hasonlóan látható, hogy

            és   ,

ezért  x3 ¹ x4 ,  és a szigorú monotonitás miatt  f(x3) ¹ f(x4) ,  tehát a fenti képlet alapján  x5  is képezhető. Továbbá

            ,

majd ugyanígy

            .

(Megjegyezzük, hogy a húrmódszer konvergenciájának bizonyításában ezen a ponton  x3  helyett  xj  áll, ahol j értéke lehet 1 vagy 2 is, és abban az esetben csak annyit tudunk, hogy

            .)

Ezt folytatva kapjuk, hogy

            , stb.

Általában

            ,

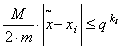ahol  k1=1,  k2=1,  és  ki=ki-2+ ki-1 ,  ha  i>2.  Emiatt  i>4  esetén  ki>i–1,  q  hatványai tehát i növelésével gyorsabban növekednek, ami biztosítja a gyorsabb konvergenciát.