Numerikus differenciálás és integrálás

Legyen példaként egy térképi vonalunk, és tekintsük ezt egy y=f(x) függvény grafikonjának. Ismeretes, hogy a differenciálható f(x) függvény-görbe xÎ[a,b] intervallumhoz tartozó s ívének a hosszát az

képlet adja meg. Ha tehát ismerjük az f(x) függvényt, akkor e képlet alapján határozhatjuk meg az s ívhosszat. A térképészeti gyakorlatban inkább az fordul elő, hogy az egyébként ismeretlen f(x) függvény értékeit bizonyos pontokban (például hosszméréssel) meg tudjuk állapítani, és ezekből az értékekből kell – közelítőleg – kiszámítani s értékét (???ábra).

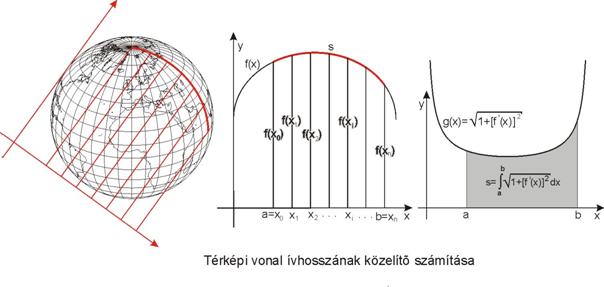
Általában adottnak tételezzük fel az ismeretlen f(x) függvény értékeit azon a=x₀, x₁, x₂, … , b=x_n pontokban, amelyek az [a,b] intervallum n részre (éspedig rendszerint egyenlő részekre) való felosztásából adódnak. Az s ívhossz mint integrál közelítőleg meghatározandó ezen x_i, f(x_i) (i=0,1, …, n) értékekből (???ábra).

A térképhasználat során a térképi hosszakon kívül egyéb térképi mennyiségek, pl. vetületi torzulások pontos kiszámításánál is szükségünk lehet függvények differenciálhányadosára és határozott integráljára, legalábbis ezek közelítő értékeire. A közelítő, másként numerikus differenciáláshoz és integráláshoz viszont a polinomos interpoláció alapjaiból indulunk ki.

Interpoláció alatt bonyolultabb függvényeknek egyszerűbb függvényekkel való közelítését értjük. Erre többnyire polinomokat használnak, de trigonometrikus függvények és racionális törtfüggvények felhasználása is előfordul. Tekintsük a polinomos interpoláció azon alkalmazását, amelynél az x₀, x₁, …, x_n pontokban adott f(x₀), f(x₁), …, f(x_n) függvényértékekhez keresünk a megfelelő pontokban ugyanazt az értékeket felvevő n-edfokú

polinomot (???ábra), vagyis:

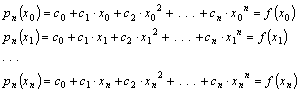
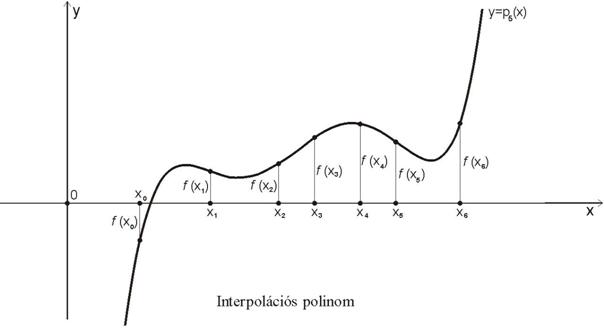
Ez egy n+1 egyenletből álló, n+1 ismeretlent tartalmazó lineáris egyenletrendszer a c₀, c₁, …, c_n együtthatókra mint ismeretlenekre nézve. Az egyenletrendszer determinánsa:

Ez egy ún. Vandermonde determináns, amely nem nulla, ha minden x_i különböző; az egyenletrendszer tehát egyértelműen megoldható. A c_i együtthatókat ki lehet számítani például a Cramer szabály alapján, de a gyakorlatban inkább más megoldásokat alkalmaznak.

Állítsuk elő a szóbanforgó interpolációs polinomot Lagrange képletével, mely olyan n-edfokú a_i(x) -szel jelölt (i=0,1,2,…,n) polinomokból (az úgynevezett alappolinomokból) indul ki, amelyek az x_i pontban 1 értéket, az összes többi x_k pontban 0 értéket vesznek fel. Könnyen meggyőződhetünk róla, hogy az

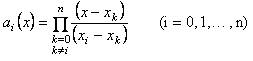
polinomok rendelkeznek mindezekkel a tulajdonságokkal. Az alappolinomok segítségével most már előállítható a p_n(x) interpolációs polinom, amely valóban átmegy az x_i, f(x_i)

(i=0, 1, …, n) koordinátájú pontokon:

Tekintsük pl. az x_i-1, f (x_i-1), az x_i, f(x_i) és az x_i+1, f(x_i+1) pontokon áthaladó másodfokú p₂(x) interpolációs polinomot:

A továbbiakban olyan interpolációs polinomokat fogunk használni, amelyeknél az x₀, x₁, …, x_n alappontok ekvidisztánsak, azaz egymástól egyenlő, h –val jelölt távolságra vannak (???ábra):

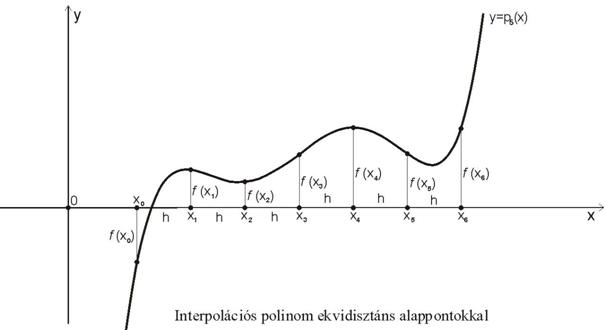
ahol

Ekkor az x_i-h, x_i, x_i+h pontokon átmenő másodfokú p₂(x) polinom az alábbi alakú:

illetve ugyanez a

vagyis az

helyettesítéssel:

(ahol x_i-h £ x £ x_i+h esetén -1 £ t £ 1) .

Ez utóbbi változatban a negyedfokú polinom a következőképpen néz ki:

Bézier-görbék

Az egymáshoz törésmentesen csatlakozó, legfeljebb harmadfokú, paraméteres megadású interpolációs polinomokat, az ún. spline-okat a számítógépes grafikában is alkalmazzák. Ezek legismertebb alakja az ún. Bézier-görbe.

Az n-edfokú Bézier-görbe a P₀ kezdőpontot és a P_n végpontot köti össze egy n-edfokú polinommal úgy, hogy az adott P₁, … , P_n-1 ún. kontrollpontok részben a görbe végpontok-beli irányát, részben a görbe haladási útvonalát határozzák meg, de ezeken általában nem halad át a görbe. A görbe pontjait a tÎ[0,1] paraméter függvényében adjuk meg: t=0 esetén a P₀ pontot, t=1 esetén a P_n pontot kapjuk meg.

Az elsőfokú Bézier-görbe a kezdő- és végponton áthaladó lineáris interpolációs polinom, vagyis a P₀(x₀,y₀) és a P₁(x₁,y₁) pontot összekötő egyenes szakasz (ld. ???ábra). A paraméteres alakja:

A másodfokú Bézier-görbe a P₀(x₀,y₀) kezdőponton és a P₂(x₂,y₂) végponton áthaladó másodfokú interpolációs polinom (parabolaív), amelynek e pontokon áthaladó érintői a P₁(x₁,y₁) kontrollpontban találkoznak (ld. ???ábra). E görbe paraméteres alakja:

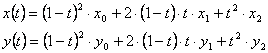
A grafikus szoftverek TrueType fontjainak karakterei másodfokú Bézier-görbékből épülnek fel.

A harmadfokú Bézier-görbe a P₀(x₀,y₀) kezdőponton és a P₃(x₃,y₃) végponton áthaladó harmadfokú interpolációs polinom (harmadfokú parabolaív), amelynek P₁(x₁,y₁) kontrollpontján a P₀(x₀,y₀) kezdőpont-beli érintő, a P₂(x₂,y₂) kontrollpontján pedig P₃(x₃,y₃) végpont-beli érintő megy át (ld. ???ábra).

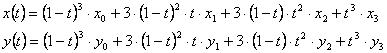
A grafikus szoftverek a sima görbe vonalakat harmadfokú Bézier-görbeívekből összeillesztett spline-okkal ábrázolják. E spline-ok törésmentességét az biztosítja, hogy az illesztési pontokban kétszer differenciálhatók.

Numerikus differenciálás

Célunk egy olyan, differenciálhatónak feltételezett f(x) függvény x_i pontbeli differenciálhányadosának közelítő meghatározása, amelynek f(x₀), f(x₁), …, f(x_n) értékeit csak egyes x₀, x₁, …, x_n pontokban ismerjük (???ábra). Ilyenkor a keresett differenciálhányadost az interpolációs polinom differenciálhányadosával közelítjük. Tételezzük fel, hogy a függvényérték az x_i-h, x_i, x_i+h helyeken sorra f(x_i-h), f(x_i), f(x_i+h). A három ponton áthaladó másodfokú polinom deriváltja a fentiek alapján:

A polinom deriváltja az x=x_i helyen:

Tehát a differenciálhányados közelítő értéke:

Többször differenciálható függvény esetén pontosíthatjuk ezt az eredményt pl. negyedfokú polinom alkalmazásával, amelyet az f(x_i-2h), f(x_i-h), f(x_i), f(x_i+h), f(x_i+2h) függvényértékekből számolunk a fenti képletből hasonló gondolatmenettel:

Végül a derivált az x=x_{i ,} vagyis a t=0 helyen:

Kiemelés után innen kapjuk a differenciálhányados pontosabb közelítését:

Numerikus integrálás

Az f(x) függvény [a,b] intervallumon vett

határozott integrálját (ami szemléletesen a függvénygörbe alatti - előjeles - területtel egyenlő, ld. ???ábra):

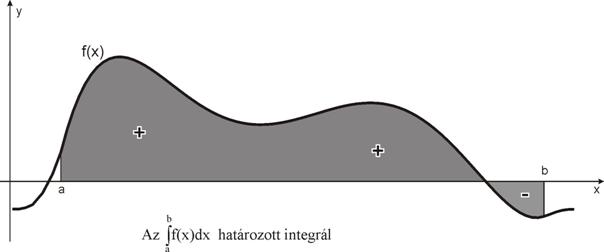
elméletileg pontosan ki lehet számítani a Newton-Leibnitz szabály segítségével:

ahol a F(x) függvény az integrálandó f(x) primitív függvénye:

.

Ha azonban a primitív függvény nem írható fel elemi függvények segítségével, vagy nem ismerjük, akkor numerikus integrálásra kerül sor.

Osszuk fel az [a,b] intervallumot n egyenlő részre, és jelöljük az osztásközök hosszát h-val:

.

Helyettesítsük az f(x) függvényt minden [x_i-1, x_i] (i=1, 2, …, n) osztásközben a lineáris interpolációs polinommal, vagyis az x_{i-1, f}(x_i-1) és az x_i, f(x_i) koordinátájú pontokat összekötő egyenes szakasszal (???ábra).

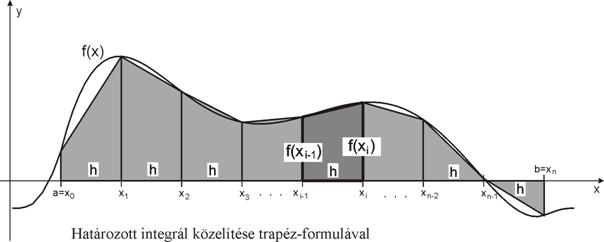
Ekkor függvény görbéje alatti terület a vizsgált osztásközben közelítőleg megegyezik egy olyan trapézzal, amelynél az alapok hossza f(x_i-1) és f(x_i), a trapéz magassága h=x_i-x_i-1. Az osztásközben számított határozott integrált a trapéz területével közelítjük:

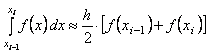
A teljes integrált az így kapott rész-integrálok összegezésével kapjuk:

A megfelelő tagok összevonásából adódik, hogy

Ez az ún. trapéz-formula.

A határozott integrál definíciója alapján könnyen belátható, hogy az osztásközök n számának növelésével a trapéz-formula a határozott integrálhoz tart, ezzel együtt természetesen a képlet számítás-igénye is növekszik. Az [a,b] intervallumban kétszer folytonosan differenciálható f(x) esetén az adott n-hez megállapítható, hogy a

trapéz-összeg eléggé megközelíti-e az integrált. Bebizonyítható ugyanis a következő hibabecslő formula:

A jobb oldalon álló képletben az n kivételével minden konstans, így n értékének megfelelő megválasztásával a szükséges pontosság elérhető. A gyakorlatban azonban az f ’’(x) függvény [a,b] intervallumbeli maximumának meghatározása hosszadalmas lehet, ezért páros n esetén kiváltható az egyszerűbb

hibabecslő képlettel, ahol a minden második osztáspont elhagyásával kapott trapéz-összeg.

A trapéz-formula hátránya főleg akkor mutatkozik meg, ha a függvény az integrálási tartományban végig konvex vagy konkáv; ebben az esetben az egyes trapézokon keletkezett hibák halmozódnak.

Hatékonyabb integrál-közelítő összeget kapunk, ha az integrálandó f(x) függvény görbéjét az [a,b] intervallumon parabola-ívekkel közelítjük. Ennek alapfeltétele, hogy az [a,b] intervallum felosztásánál a rész-intervallumok n száma páros. Kettesével összepárosítva a rész-intervallumokat, az így kapott x_i-h, f(x_i–h), x_i, f(x_i), x_i+h, f(x_i+h) pontokhoz (az i páratlan) egy másodfokú interpolációs polinomot illesztünk (???ábra):

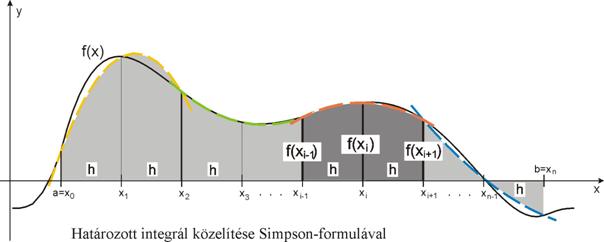
és ennek integráljával közelítjük az f(x) függvény integrálját az [x_i–h, x_i+h] rész-intervallumon:

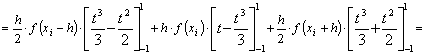
(Az helyettesítés következtében az integrandus -val szorzódott.)

A teljes [a,b] intervallumon vett integrál a rész-intervallumon vett integrálok összege, tehát

Az összevonások után kapjuk a Simpson-féle integrál-közelítő összeget:

Az előzőekhez hasonlóan a Simpson-formulából adódó s_n közelítő összegre is kapható hibabecslő formula. Négyszer folytonosan differenciálható f(x) függvény esetén belátható ugyanis, hogy

.

Ez a képlet a nevezőben álló n⁴ miatt azt mutatja, hogy – a feltételnek eleget tevő függvény esetén – a felosztás finomításával a közelítő összeg a trapéz-összegnél gyorsabban tart a határozott integrálhoz. Más szóval: megegyező számú osztáspont esetén a Simpson-formula jobb közelítést ad, mint a trapéz-formula. Az f ⁽⁴⁾(x) függvény [a,b] intervallumbeli maximumának meghatározási nehézségei miatt itt is előnyösebb egy közelítő hibabecslő képlet:

A Simpson-formula tehát kis mértékben bonyolultabb a trapéz-formulánál, de annál lényegesen hatékonyabb a határozott integrálok közelítő kiszámításában.