III.
A TÉRKÉPVETÜLETEK ALKALMAZÁSA
N)
A TÉRKÉPVETÜLETEK ALKALMAZÁSA
A GEODÉZIÁBAN
ÉS A NAVIGÁCIÓS HELYMEGHATÁROZÁSBAN
A navigációban és a
geodéziában általában pontok helyzetét határozzuk meg a tájékozódáshoz vagy a
Föld felszínén levő természetes alakzatok és mesterséges objektumok alakjának
rögzítéséhez. A pontok rögzítése történhet földrajzi koordináták vagy (az
alábbiakban méterben megadottnak
tekintett) térképi síkkoordináták segítségével. A matematikai jelölésmóddal
ellentétben a geodéziában rendszerint a középmeridián képét tekintjük x tengelynek, egyben ez jelöli ki a hálózati
É-i irányt; erre merőleges az y
tengely. A következőkben bemutatjuk azokat a fontosabb
koordinátarendszer-kialakításokat, amelyeket a leképezésekhez kapcsolódva a
geodézia és navigáció használ a fenti célokra.
a)
Magyarországi
geodéziai koordinátarendszerek
a) Budapesti
sztereografikus koordinátarendszer
A budapesti
sztereografikus rendszer alapfelülete a Bessel-ellipszoidon alapuló HD1863
dátum. A kezdőmeridián a gellérthegyi felsőrendű háromszögelési ponton megy
keresztül. A F, L ellipszoidi földrajzi
koordinátákat két lépésben („kettős vetítéssel”)
számítjuk át síkkoordinátákká (???ábra). Első
lépésben a Gauss-féle kis hossztorzulású szögtartó gömbvetülettel kapjuk az
ún. régi Gauss-simulógömbön (R = 6 378 512.966 m)
a j, l gömbi
földrajzi koordinátákat (ahol a gömbi kezdőmeridián szintén a gellérthegyi
ponton halad át):
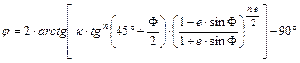
![]()
A leképezés paraméterei a
hossztartó parallelkörből (ellipszoidi szélessége Fn= 46° 32'
43,410 41", gömbi szélessége jn= 46° 30'
0,000 00") határozhatók meg:
n= 1.000 751 489 594
k= 1.003 016
135 133
Használjuk még a
számolásokhoz a Bessel-ellipszoid első excentricitását:
e= 0.081 696 683 121
57.
A második lépésben egy ferdetengelyű sztereografikus síkvetület adja
a síkkoordinátákat (???ábra). A vetületi kezdőpont a gellérthegyi felsőrendű
háromszögelési pont Gauss-gömbi képében van, melynek koordinátái:
j0Bp = 47°
26' 21,1372"
l0Bp = 0°
(E pont Bessel ellipszoidi
koordinátái Ferro-i hosszúsággal megadva:
F0Bp = 47°
29' 09,6380"
L0Bp = 36°
42' 53,5733".)
A DNy-i tájékozású síkkoordináta-rendszer
tengelyei a gellérthegyi ponton átmenő meridián és a rá merőleges főkőr
egyenesként megjelenő képei. A síkkoordinátákat a j, l földrajzi koordinátájú pontban az alábbi képletekkel számíthatjuk ki:
![]()
![]()
A
ferdetengelyű budapesti sztereografikus síkvetület inverz vetületi egyenletei is felírhatók explicit alakban. A
budapesti sztereografikus xBp,
yBp koordináták ismeretében az alábbi egyenletek
adják a gömbi j szélességet és l hosszúságot:
![]()
![]()
ahol
![]()
A gömbi földrajzi koordinátákból egy iterációs eljárás felhasználásával számíthatók ki a Bessel-ellipszoidi szélességek:
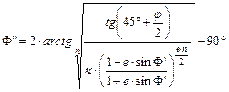
ahol a jobboldali képletbe egy F’-t behelyettesítve
kapjuk a javított F”-t. (F’ kezdőértékének a j gömbi szélességet választva, 3-4 iterációval
már kielégítő pontosság érhető el.) Az ellipszoidi hosszúság képlete:
![]() .
.
(Az inverz képletben szereplő n, k, e konstansok a direkt képletek fenti konstansaival egyeznek meg.)
A
polgári topográfiai felmérés 1857-től, a katonai topográfiai térképezés
1927-től alkalmazta a budapesti sztereografikus rendszert. A hossztorzulásokat
a ???ábra szemlélteti.
b) Marosvásárhelyi
sztereografikus koordinátarendszer
A vetületi torzulások
csökkentésére a Királyhágón túli területeken 1880-tól bevezették az ún.
marosvásárhelyi sztereografikus rendszert. A HD1863 dátumhoz illesztett régi
Gauss-simulógömbről egy új síkra vetítettek (???ábra). Ennek vetületi
kezdőpontja a Marosvásárhelytől ÉNy-ra fekvő Kesztej-hegy háromszögelési pont gömbi
képe (Fasching Antal számítása alapján):
j0Mvh= 46°
l0Mvh= + 5° 20’ 41,8290” a gellérthegyi meridiántól K-re.
(Ugyanennek a pontnak a
Bessel-ellipszoidi koordinátái Ferro-i hosszúsággal:
ΦnMvh =
46° 33' 06,4273"
ΛnMvh = 42° 03' 20,9550" .)
A síkkoordinátarendszer
DNy-i tájékozású. A síkkoordináták képletei:
![]()
![]()
ahol
![]() .
.
A
marosvásárhelyi sztereografikus xMvh,
yMvh koordináták ismeretében az alábbi inverz
vetületi egyenletek adják a gömbi j szélességet és l hosszúságot:
![]()
![]()
ahol
![]() ,
,
és
![]() .
.
A hossztorzulásokat a
???ábra mutatja.
g) Katonai
sztereografikus koordinátarendszer
A negatív előjelű
koordináták kiküszöbölése céljából 1936-ban bevezették a katonai sztereografikus koordinátarendszert az origó 500 000 m-rel
D-re és 500 000 m-rel Ny-ra való eltolásával, valamint a
koordinátatengelyek irányának megfordításával, ami ÉK-i tájékozást eredmények.
A budapesti és a katonai sztereografikus koordináták közötti összefüggések
tehát:
![]()
![]()
A marosvásárhelyi rendszer
origóját 600 000 m-rel D-re és 600 000 m-rel Ny-ra tolták el, és a
tájékozást szintén ÉK-ire változtatták. A marosvásárhelyi és a katonai
sztereografikus koordináták közötti összefüggések:
![]()
![]() .
.
d) Ferdetengelyű
szögtartó hengervetületi koordinátarendszerek
Az 1908-ban polgári
célokra bevezetett ferdetengelyű szögtartó hengervetület alapfelületének
helyzete (a Bessel-ellipszoidon alapuló HD1909 dátum) csak kis mértékben tér el
a sztereografikus vetület dátumának rendszerétől. Ugyanis bevezetésekor a
Gellérthegy kezdőpontban az onnan kiinduló háromszögoldalak azimutját
megváltoztatták. Emiatt a hálózat helyzetének változása értelmezhető az e pont
körüli 6,44’’-es az óramutató járásával megegyező irányú elforgatásaként
(???ábra). A F, L ellipszoidi földrajzi
koordinátákat e vetületben is kettős leképezésnek vetjük alá (???ábra), azaz
azokat először a Gauss-féle kis hossztorzulású szögtartó gömbvetülettel képezünk
le a régi Gauss-simulógömb j, l koordinátáira.
(A L és l hosszúságokat
itt is a gellérthegyi kezdőmeridiántól számítjuk.) A leképezés függvényeinek
képletei és paraméterei megegyeznek a sztereografikus vetületnél használtakkal.
A gömbi
koordinátákból a síkba képezés – a korabeli országterülethez igazodva – három ferdetengelyű
szögtartó hengervetülettel történik (???ábra): egy É-i (Hengervetületi Északi
Rendszer, röviden HÉR), egy középső (Hengervetületi Középső Rendszer, röviden
HKR) és egy D-i sávot (Hengervetületi Déli Rendszer, röviden HDR). A
gellérthegyi kezdőmeridián (lK=0.0°) a térképen egyenesként jelenik
meg, ez az x tengely. Mindhárom
hengervetület vetületi kezdőpontja a kezdőmeridián képén van, az alábbi gömbi
szélességeknek megfelelő pontokban:
a HÉR-ben jK=48° 40’ 2.0”;
a HKR-ben jK=47° 06’ 0.0”;
a HDR-ben jK=45° 31’ 59.0”.
A
gellérthegyi meridiánra e pontokban merőleges főkörök (a segédegyenlítők)
szintén egyenesekre képeződnek le, ezek alkotják az y tengelyeket. Mind a három rendszer DNy-i tájékozású.
Az xH,
yH hengervetületi
koordinátákat az alábbi vetületi egyenletek adják (továbbra is
R =
6 378 512.966 m):
![]()
és
![]()
Ha ismerjük az xH,
yH hengervetületi
síkkoordinátákat, akkor a gömbi j, l földrajzi
koordinátákat az
alábbi inverz vetületi egyenletekből kapjuk:
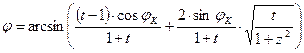
és
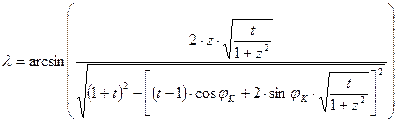 ,
,
ahol
![]()
és
![]()
![]() .
.
A vetület megalkotása során az előbbi képletek mellett matematikai sorokkal is megadták az x, y, F, L koordinátákat, valamint a vetületi meridiánkonvergenciát.
E vetületben
a segédegyenlítők hossztartók. Innen É és D felé távolodva a hossztorzulások
(valamint a területtorzulások) nőnek (???ábra).
A HÉR, HKR és HDR rendszerű kataszteri térképek szelvényezése nem fokhálózati vonalak, hanem a térképi síkkoordináta-vonalak mentén történt.
e) Az Egységes Országos Vetület
koordinátarendszere
Az Egységes Országos
Vetület (EOV) az 1970-es évek közepén polgári topográfiai célokra létrehozott
Egységes Országos Térképrendszer (EOTR) vetülete. Alapfelülete az IUGG’67
nemzetközi ellipszoidon alapuló HD72 dátum. Az ellipszoidi földrajzi
koordinátákból kettős leképezéssel jutunk az EOV síkkoordinátákhoz (???ábra).
Első lépésben az alapfelületről az ún. új Gauss-simulógömbre (R=6379743m) képezünk le a
Gauss-féle kis hossztorzulású szögtartó gömbvetülettel:
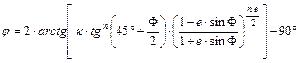
![]()
A leképezés paramétereit a
hossztartó parallelkörből (ellipszoidi szélessége Fn= 47° 10'
0,0", gömbi szélessége jn= 47° 07' 20,05780") számíthatjuk ki:
n= 1,000 719 704 936
k= 1.003 110 007 693
A számolásoknál használjuk
az IUGG’67 ellipszoid első excentricitását:
e= 0.081 820 567 9407.
Mind a L ellipszoidi, mind a l gömbi hosszúságot
a Gellérthegy ponton átmenő kezdőmeridiántól számítjuk.
A gömbi földrajzi koordinátákból a térképi síkkoordinátákat a 0.99993 tényezővel redukált ferdetengelyű szögtartó hengervetület segítségével kapjuk (???ábra). A segédegyenlítő – a gellérthegyi meridiánra a
jK=47° 6’ 0.0”
gömbi szélességű pontban merőleges főkör – a kezdőmeridiánhoz hasonlóan egyenesre képeződik le. Ezen egymásra merőleges egyenesek képezik az ÉK-i tájékozású térképi síkkoordináta-rendszer alapját. Az origónak tekintett metszéspontjukat eltoljuk 650000 m-rel Ny-ra és 200000 m-rel D-re, így minden síkkoordináta pozitív előjelű lesz, és a magyarországi pontok X koordinátái 400000 m-nél kisebbek, Y koordinátái pedig 400000 m-nél nagyobbak. Ezek alapján a vetületi egyenletek:
![]()
és
![]() .
.
Az X és Y EOV síkkoordináták ismeretében az inverz
vetületi egyenletekkel kapjuk a gömbi földrajzi koordinátákat:
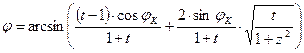
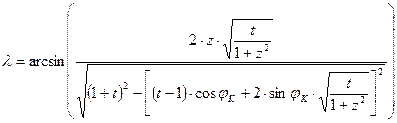 ,
,
ahol
![]()
és
![]()
![]() .
.
Az EOV-ben két segédparallelkör
torzulásmentes, melyek között a hossz- és a területtorzulás 1-nél kisebb, az
ezeken kívüli területeken 1-nél nagyobb; az ország területén fellépő legnagyobb
hossztorzulás az egységtől csak 10-4 nagyságrendben tér el (???ábra).
Az EOTR kataszteri és
topográfiai térképek szelvényezése szintén a síkkoordináta-vonalak mentén
történik.
b)
Nemzetközi geodéziai
és topográfiai koordinátarendszerek
a) A
Gauss-Krüger vetület koordinátarendszere
Bontsuk fel a Kraszovszkij ellipszoid alapfelületet a
dátumválasztótól kiindulva összesen 60 db 6°-os ellipszoidi kétszögekre (ún.
zónákra), és minden ilyen kétszöget képezzünk le a Gauss-Krüger vetülettel. E
zónákat K-i irányba haladva sorszámozzuk, így A Greenwich-i meridiántól K felé
kezdődik a 31. zóna. Magyarország területe a 33. és 34. zónára esik, e kettőt a
18° hosszúsági kör választja el (???ábra). Minden zónának önálló
síkkoordináta-rendszere van. A középmeridián és az egyenlítő egymásra merőleges
egyenesekre képeződik le. Az egyenlítő képe lesz az Y tengely, a középmeridián képét pedig – a
negatív Y koordináták kiküszöbölése céljából – 500000 m-rel
Ny felé eltolva kapjuk az X tengelyt.
Minden zónát az
egyenlítőtől É-ra és D-re kiindulva 4°-os sávokra bontanak fel. Egy ilyen
4°x6°-os foktrapézt 1:1000000 méretarányú térképszelvényen ábrázolnak, és az
ABC betűivel jelölik meg, szükség esetén az északi félgömbön az N, a déli
félgömbön az S kezdőbetűvel kiegészítve. Magyarország így a 33-as zóna a 33-L
és 33-M, valamint a 34-es zóna 34-L és 34-M jelű szelvényeire esik (???ábra).
L0-lal
jelölve a zóna középmeridiánját, a F, L ellipszoidi koordinátákból az alábbi vetületi egyenletekkel kapjuk a
térképi síkkoordinátákat:
![]()
![]()
ahol az
![]()
integrál numerikusan
kiszámítható, vagy közelíthető az alábbi sorral:
![]()
![]()
(Kraszovszkij
ellipszoid esetén a=6 378 245
és e2=0.0066934275). A többi Ai (i=1,2,…,6) együttható a F
szélesség függvényében:
![]()
![]()
![]()
![]()
![]()
![]() ,
,
ahol
![]() .
.
Az
általában ötjegyű YGK koordináta elé
még odaírják a zóna sorszámának második számjegyét, ez az ún. vezérszám. A magyarországi pontok
Gauss-Krüger Y koordinátái tehát vagy 3-as vagy 4-es
számjeggyel kezdődnek attól függően, hogy a pont a 33-as vagy a 34-es zónában
fekszik.
Az YGK ,
XGK Gauss-Krüger
koordinátákból kiszámíthatók az ellipszoidi földrajzi koordináták, amihez
az YGK ,
XGK pontból a
középmeridián képére bocsátott merőleges T
talppontjához tartozó FT „talpponti
szélességből” indulunk ki (???ábra). Ez megkapható az
![]()
nemlineáris egyenlet megoldásából, vagy pedig az
![]()
sorból, ahol
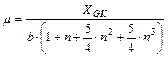
és
![]()
(Kraszovszkij ellipszoid esetén b=6 356 863
m).
A F, L földrajzi koordináták most az
![]()
![]()
inverz vetületi
egyenletekből adódnak, ahol
![]()
![]()
![]()
![]()
![]()
![]()
és
![]() .
.
Megjegyezzük, hogy az YGK koordináta első számjegye a vezérszám, így azt a számolásnál nem kell figyelembe venni.
A torzulásmentes
középmeridiántól távolodva a hossz- és területtorzulások nőnek. Egy 6°-os zónán
belül a torzulás legnagyobb az egyenlítő és a határoló meridiánok
találkozásánál (lmax»1.0013), ezért geodéziai célokra 2°-os (lmax»1.00015) és 3°-os (lmax»1.00034) zónákat is használnak. Magyarország területén
a 18°-os szegélymeridiánon fellépő legnagyobb hossztorzulás: lmax»1.00068).
b) Az
UTM vetület koordinátarendszere
Az alapfelület 6°-os ellipszoidi kétszögekre (zónákra) való
bontása után minden zónának a 80° D-i szélességtől a 84° É-i szélességig
terjedő területe UTM vetületben kerül ábrázolásra. A zónák sorszámozása a
Gauss-Krüger rendszerhez hasonlóan 1-től 60-ig történik. Minden zóna 8°-os foktrapézokra
bomlik (az utolsó övezet a 72° és a 84° É-i szélesség között 12°-os). Egy ilyen
foktrapézt 4 db 1:1000000 méretarányú térképszelvényen ábrázolnak. Ezeket a
zónasorszám után álló nagybetűvel (angol ABC) jelölik C-től X-ig (az I és az O
betű kimarad). A D-i pólusnak a 80° D-i szélességig terjedő területe UPS
síkvetületben van ábrázolva, ennek két félkör alakú részét A-val és B-vel
jelölik. Az É-i sarok környékének térképe a 84° É-i szélességtől hasonlóan UPS (Universal
Polar Stereographic) vetületű, és ennek két felét Y-nal és Z-vel jelölik.
Magyarország területe a 33T, 33U, 34T, és 34U jelű 8°x6°-os foktrapézra esik
(???ábra).
A függőleges
koordinátatengely itt is el van tolva 500000 m-rel Ny-ra (???ábra). A Hayford
ellipszoidi, vagy újabban a WGS’84 koordinátákból közvetlenül megkapjuk az UTM síkkoordinátákat
(Universal Transverse Mercator Grid) a Gauss-Krüger koordináták 0.9996-tal való
beszorzásával és az eltolások figyelembevételével:
![]()
![]()
(WGS’84 ellipszoid esetén
a képletekben a=6 378 137
és e2=0.00669438006.)
Az inverz vetületi
egyenletek az YUTM , XUTM
síkkoordinátákból adják az ellipszoidi koordinátákat úgy, hogy a Gauss-Krüger
vetületekre vonatkozó egyenletekbe az
![]()
![]()
helyettesítéseket végezzük el. (WGS’84 alapfelület esetén
b=6 356 752,3142 m.)
A 6°-os UTM zóna középmeridiánján a legkisebb a
hossztorzulási modulus (lmin»0.9996), az egyenlítő és a határoló meridián
találkozásánál pedig a legnagyobb (lmax»1.001). Magyarország területén a 18°-os
szegélymeridiánon fellépő legnagyobb hossznagyobbodás: lmax»1.00028.
c)
Katonai azonosító
(jelentő) rendszerek
E rendszerek bármely
földrajzi helyhez hozzárendelnek egy kódot, amely segítségével a földrajzi helyet
– elsősorban katonai vagy navigációs célból – nagy pontossággal azonosítani
lehet.
a) Az
MGRS keresőhálózat
Az MGRS (Military Grid
Reference System) keresőhálózat egyrészt az UTM zónarendszerére épülő 8°x6°-os
foktrapéz-felosztáson, másrészt az UTM síkkoordináta-rendszeren alapul, és
segítségével vagy egy 100 km x 100 km-es térképi négyzetet, vagy ezen belül egy
térképi pontot lehet megjelölni. Egy
6°-os UTM zóna mintegy 667 km széles. Az UTM 500000 m-es Y koordinátavonala a középmeridiánnal
esik egybe, ettől K-re és Ny-ra 4-4 db 100000
m széles oszlop az egész zónát tartalmazza. A zónát a 0 m-es UTM
X koordinátájú egyenlítővel párhuzamosan is
felbontják 100000 m-es sorokra az X koordinátavonalak mentén, tekintet nélkül a foktrapéz-
felosztásra. Az oszlopok és a sorok együttesen egy 100 km x 100 km-es
négyzethálót hoznak létre.
A 6°-os UTM zónákat
hármasával összevonják és a zónánként 8 db 100000 m-es oszlopot együttesen jelölik,
éspedig az angol ABC nagybetűivel Ny-ról K felé, A-tól Z-ig (az I és az O betű
itt is kimarad). Az egyes zónákban az egyenlítőtől É-ra és D-re elhelyezkedő
100-100 db 100000 m-es sorok jelölése szintén az angol ABC betűivel történik. A
páratlan sorszámú zónákban a sorokat az egyenlítőtől mindkét irányba kiindulva –
5-ször ismétlődően – A-tól V-ig jelölik (az I és az O itt is kimarad). A páros
sorszámú zónákban a sorok jelölése az egyenlítőtől mindkét irányba kiindulva: FGHJ…UVABCDE (az I és az O itt is kimarad), és
mindez a pólusig 5-ször ismétlődik.
Az MGRS azonosító három
részből áll:
-
a 8°x6°-os
foktrapéz azonosítója (zónasorszám+övezeti betűjel, pl. 34T);
-
a 100 km x 100 km-es
négyzet azonosítója (oszlop betűjele + sor betűjele, pl. CT);
-
a négyzeten belül
a m-re kerekített UTM síkkoordináták utolsó öt számjegye (Y koordináta + X
koordináta, összesen 10 számjegy, pl. 34T CT 54053 59662).
Az MGRS azonosítóból
helyreállítható a pont UTM síkkoordinátája, mert a 100 km x 100 km-es négyzet
azonosítójából megállapítható a bal alsó sarok 100000 m-re kerek Y és X UTM
koordinátája, amihez hozzáadandó az utolsó 5-5 számjegy.
Magyarország területe a
31-33-as összevont zónák K-i szélén a W, X és Y jelű oszlopokban, valamint a
34-36-os összevont zónák Ny-i szélén a B, C, D, E és F jelű oszlopokban
helyezkedik el.
b) A
GEOREF keresőhálózat
A
GEOREF (World Geographic Reference System) keresőháló a földrajzi fokhálózat
segítségével bontja fel a Föld felületét mind kisebb foktrapézokra, ami alapján
földi területeket lehet megjelölni.
Az elsődleges felbontás 24 db 15°-os kétszögre történik, amelyeket a
dátumválasztó vonaltól K felé indulva az angol ABC nagybetűivel jelöljük A-tól
Z-ig (az I és az O betű kimarad). Minden ilyen kétszöget 15°-onként felvett
szélességi körökkel tovább bontunk foktrapézokra, ilyen módon keletkezik a földnek
egy 15°x15°-os felbontása ún. mezőkre
(???ábra). A 12 db 15°-os övezetet D-ről É felé haladva A-tól M-ig az angol ABC
nagybetűivel jelöljük (az I és az O betű kimarad). A két betű együttesen
azonosítja a 15°x15°-os mezőt. Magyarország a PK jelű mezőben fekszik.
A
15°x15°-os mezők tovább bomlanak 1°x1°-os almezőkre, melyek kétbetűs
azonosítójából az első betű Ny-K-i irányban adja meg az 1°-os oszlopot (A-tól
Q-ig, I és O kimarad), a második pedig D-ről É felé haladva adja meg az 1°-os
sort (szintén A-tól Q-ig, I és O kimarad). Budapest pl. a PK jelű mező EC jelű almezőjében
található.
Az
1°x1°-os almezők még kisebb, 1’x1’-es almezőkre bonthatók, amelyeket a DNy-i
sarokpont földrajzi hosszúságának és szélességének perceivel azonosítunk.
Eszerint a (47° 26’
22” É, 19° 15’ 43”
K) földrajzi koordinátákkal meghatározott „Liszt Ferenc Airport 2” 1’x1’-es
almezejét 15 26
–tal jelöljük. Az almező teljes azonosítója tehát: PK EC 15 26.
A
földi hely megadása tovább pontosítható, ha az almezőket tizedpercekkel vagy századpercekkel
adjuk meg. Előbbi esetben az azonosító három-három számjegyet, utóbbi esetben
négy-négy számjegyet tartalmaz.
A GEOREF keresőhálót az Egyesült Államok légiereje számára fejlesztették ki, a léginavigáció használja.