A VETÜLETEK ALAP- ÉS
KÉPFELÜLETE
Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai
A
geodézia, a térinformatika és a térképészet a görbült földfelületen
elhelyezkedő geometriai alakzatokat (pontokat, vonalakat vagy felületdarabokat)
helyhez kötéssel azonosít és/vagy síkban ábrázol. Az ennek során megkövetelt
pontosságtól függően választjuk meg a lokalizáláshoz illetve az ábrázoláshoz
használt felületet. Kis terület esetén maga a földfelszín is többnyire
elfogadható pontossággal közelíthető síkkal.
Nagyobb terület esetén a földalak görbültsége már nem hagyható figyelmen kívül.
A megkövetelt pontosságtól függően közelíthetjük a tényleges földalakot gömbbel, a sarkoknál fellépő lapultságot
is figyelembe vevő forgási ellipszoiddal,
vagy az elméleti földalakkal – az átlagos tengerszinttel egybeeső nehézségi
szintfelülettel – a geoiddal.
Bármilyen
felületen történjék is az alakzatok lokalizálása, a megjelenítés gyakorlatilag
mindig síkban történik, legyen szó akár papírtérképről, akár képernyőtérképről.
Emiatt a minden irányban görbült felületen lokalizált objektumokat az ábrázolás
előtt rendszerint síkra képezik le olymódon, hogy a síkbeli méretviszonyok
(hosszak, irányok ill. szögek, területek nagysága) a földfelületi
méretviszonyoktól kevéssé térjenek el, és így azokra térképi mérések alapján
vissza lehessen következtetni. A kiindulási – görbült – felületet alapfelületnek, a hozzárendelési
(általában sík) felületet képfelületnek,
a leképezést vetületnek nevezzük.
Előírjuk,
hogy mind az alapfelület, mind a képfelület lehetőleg folytonos,
szabályos és zárt matematikai képlettel (esetleg sorral) leírható legyen (Minthogy a geoid-felületre az utóbbi két feltétel
nem teljesül, így az a vetületi vizsgálatoknak közvetlenül nem képezi tárgyát.)
A felületek zárt képlettel való leírása általában a derékszögű x,y,z koordináták közötti összefüggések megadásával
történik. Ezek az összefüggések megadhatók
egyenletként, függvény
formájában vagy paraméteres alakban.
a) A
felületek
![]()
egyenlete egy skalár-vektor függvény
nívófelületét jelenti. A sík egyenlete pl.:
![]()
Az R sugarú, origó-centrikus gömb
egyenlete:
![]()
A z
forgástengelyű, origó-centrikus forgási ellipszoid z irányú féltengelyét b-vel, a másik (elforgatott)
féltengelyét a-val jelölve, kapjuk az
![]()
egyenletet.
b) A
kétváltozós
![]()
függvény-alak az egyenlet-alak speciális
esetének tekinthető. Hátránya, hogy egyes felületek csak többértékű függvénnyel
írhatók le. A síkot ebben az esetben a
![]() ,
,
a
gömbfelületet a
![]() ,
,
a
forgási ellipszoidot a
![]()
függvény
adja meg.
c) Az
ún. paraméteres alak esetében a
felület pontjainak x, y, z koordinátáit
az u,v valós paraméterek folytonos
függvényeként adjuk meg:
![]()
A v paraméter rögzített értékeinél a
felületen a folytonos u-vonalak
seregét, az u paraméter rögzített
értékeinél a folytonos v-vonalak
seregét kapjuk. Ezek az ún. paramétervonalak
a felületet egyrétűen fedik le (??? ábra). A felület minden pontján áthalad egy
u- és egy vele nem párhuzamos v-vonal.
Sem az u-vonalak, sem a v-vonalak nem metszhetik egymást. A sík
paraméteres alakja:
![]()
A
gömb paraméterezhető pl. az
![]()
alakban.
A pólusokat a z tengelyen felvéve, az u
paraméter itt megfelel a közismert j földrajzi szélességnek, v
pedig a l földrajzi hosszúságnak.
A
forgási ellipszoid egyik lehetséges paraméteres felírása:
![]()
(Ez
előállítható az R sugarú gömbből a/R-szeres
hasonlósági transzformációval, majd b/a-szoros, z irányú merőleges affinitással.)
A
forgási ellipszoid felület méreteit a féltengelyek a és b
hossza egyértelműen meghatározza. A felület lapultsága miatt a>b,
a lapultság mértékét az
![]()
mérőszám,
az ún. lapultság, vagy az
![]()
ún.
első excentricitás adja meg. E két
mérőszám kapcsolatát az
![]()
egyenlet
adja meg. Fordítva az
![]()
egyenlet
megoldásából:
![]()
amelynél
– tekintve, hogy a lapultság értéke 1-nél nagyobb nem lehet – csak a „–” előjel jó. Vagyis
![]()
Szokás
még definiálni az e’ ún. második excentricitást:
![]()
Képfelület
a síkon kívül lehet ún. síkbafejthető
felület is, amely a rajta lévő felületi görbék ívhosszának megváltozása
nélkül síkká transzformálható. Ilyen pl. a forgáskúp palástja, vagy a
forgáshenger palástja. Az ívhosszak változása egyébként maga után vonja a
felület többi belső méretviszonyának – így a felületi szögeknek és területeknek
– a síkbafejtés során bekövetkező változatlanságát is.
Magától
a leképezéstől elvárjuk, hogy
- létesítsen kölcsönösen
egyértelmű (injektiv) megfeleltetést az alap- és a képfelület pontjai
között az ábrázolandó területre vonatkozólag;
- legyen lehetőleg
egyetlen zárt matematikai képlettel (esetleg sorral) leírható;
- legyen az ábrázolandó
terület minden pontjában kétszer folytonosan differenciálható.
A
leképezési függvényeket vetületi
egyenleteknek hívják.
Paraméterek az alap- és a képfelületen
Az alapfelület paraméterezése – a földrajzi koordinátarendszer
Mind
a gömb-, mind a forgási ellipszoid-felületi pontokat meg lehet adni térbeli derékszögű koordinátákkal. Ekkor
a koordinátarendszer origóját célszerűen az alapfelületi alakzat középpontjában
vesszük fel; a z tengely a polártengellyel
esik egybe, az x tengelyt pedig rendszerint
a kezdőfélsík iránya jelöli ki. Az egyenlítő
síkja ekkor az xy síkra esik. Alkalmazásuk
akkor előnyös, ha alapfelületi és alapfelületen kívüli pontok kapcsolata kerül
előtérbe (pl. a GPS működése során). Hátrányuk, hogy egy pont koordinátáiról
nem ismerhető fel közvetlenül, hogy az alapfelületen van-e, illetve a
derékszögű koordináták kis megváltozása is az alapfelület elhagyásához vezethet.
A
gömb- és a forgási ellipszoid alapfelület szokásos paraméterezése mégis a földrajzi koordinátarendszer. Ez az
alakzat középpontjában felvett origójú térbeli
polárkoordináta-rendszeren alapul, melynek polártengelye kijelöli az (É-i)
pólust (???ábra).
A földrajzi szélesség
Gömb alapfelület esetén vegyünk fel egy tetszőleges
alapfelületi P pontot. Az origótól a P-hez vezető rádiuszvektornak a
polártengellyel bezárt b szöge (a pólustávolság), illetve ennek pótszöge,
a rádiuszvektornak a polártengelyre merőleges síkkal bezárt szöge a j(=90°-b) földrajzi szélesség adja az egyik paramétert. (Megjegyezzük, hogy e
rádiuszvektor egyben merőlegesen metszi az alapfelületet.) A koordinátarendszer
kezdő-félsíkja (melynek határa a polártengelyre esik) a gömbfelületen kijelöli
a kezdőmeridiánt. Most az
alapfelületi P pontot tartalmazó, a polártengely által határolt félsíknak a
kezdő-félsíkkal bezárt szöge adja a másik paramétert, a l földrajzi
hosszúságot. (A harmadik polárkoordináta, a rádiuszvektor R hossza, amely megegyezik a gömb
sugarával, minden P pontra azonos, így ez a P pont megadásánál figyelmen kívül
hagyható.)
Az
egyik paraméter rögzítésével és a másik változtatásával jutunk a gömbfelület paramétervonalaihoz.
Az azonos földrajzi szélességű (vagy azonos pólustávolságú) pontok által
meghatározott gömbi körök a szélességi
körök vagy parallelkörök. (Ezek
között kitüntetett szerepet játszik a 0°-os szélességi kör, az egyenlítő.) A j földrajzi szélességet
előjellel látjuk el, amelyet az É-i félgömbön tekintünk pozitívnak (vagyis –90°£j£90°, és 0°£b£180°). Az R sugarú gömbön a j szélességi kör r sugara:
![]()
az
egyenlítő sugara így R. A l földrajzi hosszúságot a K-i
féltekén tekintjük pozitívnak (vagyis -180°£l£180°). Az azonos földrajzi
hosszúságú pontok által meghatározott gömbi főkörívek (félkörök) a hosszúsági körök vagy meridiánok. A hosszúsági kör sugara
mindig R.
A
kezdőmeridiánnal nem keverendő össze a középmeridián,
amely az ábrázolt terület középvonalában haladó, többnyire kerek értékű
hosszúsági kör. Ez általában a térképi fokhálózat szimmetriatengelye, így a
képfelületen egyenesként jelenik meg.
Forgási ellipszoid alapfelület esetén a földrajzi
szélességet többféle meggondolás alapján is lehet értelmezni, amelyek mind a
gömbi földrajzi szélesség általánosításai. A térbeli polárkoordinátarendszer
segítségével kapott definíció szerint a Y geocentrikus
szélesség az origóból az ellipszoidfelületi P ponthoz vezető
rádiuszvektornak a polártengelyre merőleges síkkal bezárt szöge (???ábra).
Ettől különbözik a forgási ellipszoid fenti paraméteres alakján alapuló j redukált
szélesség, amely a P pontból az ellipszoid-felületre alkalmazott z irányú a/b-szeres
merőleges affinitással kapott (gömbfelületi) P’ pont gömbi szélessége
(???ábra). Végül az ellipszoidi F geodéziai
szélességet az ellipszoidfelület P pontbeli normálisának a polártengelyre
merőleges síkkal bezárt szögével definiáljuk (???ábra). Könnyű belátni, hogy gömbfelületi
(a=b)
P pont esetén mind a
geocentrikus, mind a redukált, mind pedig a geodéziai szélesség ugyanazzal a j gömbi szélességgel egyezik meg.
Ezen
lehetőségek közül ellipszoidi földrajzi szélességnek azt célszerű tekinteni,
amely a fizikai földfelszínen legalábbis közelítőleg mérhető. Ha a geoid
valamely P pontjában a geoid normálisa (a nehézségi erő irányát megadó
függővonal) és a Sarkcsillag irányára merőleges sík (az egyenlítő síkja) által
bezárt FA szöget (az ún. csillagászati
vagy asztronómiai szélességet) csillagászati
eszközökkel lemérjük, akkor az a F geodéziai
szélességgel közelítőleg meg fog
egyezni. Ebből a megfontolásból az
ellipszoidi földrajzi szélességet a F geodéziai szélességgel definiáljuk. Ennek pótszöge a B geodéziai
pólustávolság: B=90°–F. A közelítés hibáját egyrészt
a szabálytalan geoidfelület merőlegesének az ellipszoid-felületi merőlegestől
való eltérése (az ún. függővonal-elhajlás),
másrészt az ellipszoid forgástengelyének a Sarkcsillag irányával bezárt szögkülönbsége
adja.
Az
azonos F földrajzi szélességű pontok
itt is egy szélességi kör vagy parallelkör mentén helyezkednek el,
melyek előállíthatók az ellipszoidfelület forgástengelyre merőleges
körmetszeteként. A továbbiakban szükségünk lesz a paramétervonalak geometriai
jellemzőire.
A F földrajzi szélességű
parallelkör r sugarának és az
egyenlítőtől való z távolságának
meghatározásához tekintsük a forgási ellipszoid egy – a forgástengelyt
tartalmazó – síkmetszetét (???ábra), amely egy ellipszis (ún. bimeridián). Írjuk fel a tengelyek által
alkotott r,z koordinátarendszerben a
bimeridián kanonikus egyenletét:
![]()
Innen
pl. a felső ív által megadott függvény:
![]() és
és ![]()
Másrészt
a függvény r -beli deriváltja megegyezik a függvénygörbe (r,z) pontbeli érintőjének iránytangensével. Az érintő az r
tengellyel bezárt szöge –(90°–F), ezért
![]()
Tehát
![]()
Négyzetreemelés
után innen r kifejezhető:
![]()
(Az
egyenlítő sugara tehát a.)
r képletét behelyettesítve az
ellipszis kanonikus egyenletébe, z kifejezhető:
![]()
Vagyis
![]()
Most
már meghatározhatók az egyes ellipszoidi szélességek közötti összefüggések. A
???ábrából:
![]()
A
forgási ellipszoidból a/b-szeres merőleges affinitással a
sugarú gömböt kapunk, eközben a geocentrikus szélesség egyik szögszárát képező
rádiuszvektor a redukált (gömbi) szélesség szárába megy át, vagyis
![]()
A
két utóbbi egyenlőségből
![]()
következik.
Egy
síkgörbe simulókörének azt a kört
nevezzük, amelynek a P0 közös pontban mind az első
deriváltja (tehát a P0 pontbeli érintő
iránytangense), mind a második deriváltja megegyezik a görbéével. (Egy kör
bármely pontbeli simulóköre természetesen sajátmagával esik egybe.)
Vizsgáljuk
az ellipszoidfelületi P ponton áthaladó összes – a forgási ellipszoid
síkmetszeteként keletkező – felületi görbe P pontbeli simulókörének sugarát, az
ún. görbületi sugarat. Meusnier
ismert tétele szerint: ha arányba állítjuk a P ponton átmenő (F szélességű) parallekör r
sugarát (a „ferdemetszet” görbületi sugarát), valamint a meridiánra merőleges
sík ellipszoidfelülettel alkotott metszésvonalának (a „normálmetszetnek”) a P
pontbeli görbületi sugarát – az N(F) ún. harántgörbületi sugarat, eredményként a két sík által bezárt szög
(esetünkben az ???ábráról leolvashatóan a F szélesség) cosinus-át kapjuk:
![]()
Innen r ismeretében az N(F) kifejezhető:
![]()
Az ???ábrán az
r befogójú és
F szögű derékszögű háromszög
átfogója éppen
![]()
Innen
![]()
Az N(F) a z képletébe is behozható:
![]()
A földrajzi hosszúság
Az
ellipszoidi L földrajzi hosszúságot – az ellipszoid
centrumából mint origóból kiinduló és az ellipszoidfelület forgástengelyével
egybeeső polártengelyű térbeli polárkoordináta-rendszerből kiindulva – a
gömbhöz hasonlóan, a P pontot tartalmazó félsíknak a kezdő félsíkkal alkotott
(előjeles) szög segítségével definiáljuk. A fizikai földfelszínen a hosszúság
szintén mérhető csillagászati eszközökkel, éspedig a pontbeli és a Greenwich-i
delelés időpontjának különbségéből: 1 óra eltérés megfelel 15° hosszúságkülönbségnek.
Az azonos L földrajzi hosszúságú pontok
egy fél-ellipszis alakú meridiánt
határoznak meg, melynek féltengelyei a
és b.
Írjuk
fel az (r,z) síkban az
origó-centrikus meridián-ellipszis egy adott r0,z0 koordinátájú
pontjában a simulókör sugarát a F0 szélesség függvényében (??? ábra). A meridián-ívet pl.
a
![]()
függvény
alakban adjuk meg. Az (egyelőre ismeretlen)
r sugarú, (u,v) középpontú simulókör szintén
függvény alakban:
![]()
A
fenti definíció az alábbi három egyenlethez vezet:
1.) ![]() (az r0,z0 pont a két
alakzat közös pontja)
(az r0,z0 pont a két
alakzat közös pontja)
2.) ![]() (az r0,z0 pontban a
két alakzat érintője közös)
(az r0,z0 pontban a
két alakzat érintője közös)
3.) 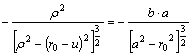 (az r0,z0 pontban a
második deriváltak egyenlők)
(az r0,z0 pontban a
második deriváltak egyenlők)
A
2.) egyenletből r0–u
kifejezhető:
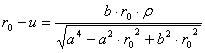
Ezt
behelyettesítjük a 3.) egyenletbe, majd ebből kifejezzük r -t:
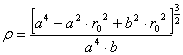
Végül
az
![]()
helyettesítéssel
kapjuk, hogy
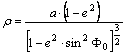
(Itt
felhasználtuk a
![]()
azonosságot.)
A
meridián-ellipszis görbületi sugara tehát a szélesség változásával pontról
pontra változik. Ezt a függvényt nevezzük meridiángörbületi
sugárnak, amelyet szokásosan M(F)-vel jelölünk:
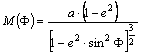
A
földi ellipszoidok lapultsága miatt a meridiángörbületi sugár legkisebb az
egyenlítőnél, legnagyobb a pólusnál.
A
földrajzi hosszúság kezdőfélsíkját illetve az általa kimetszett kezdőmeridiánt
a felmérés kiterjedésétől függően nem csak globálisan, hanem helyileg is
rögzíthetik. A geokartográfiában és a topográfiai térképműveknél általában
Greenwich-i kezdőmeridiánt használnak. Régebben - főleg Európában - elterjedt
volt a Ferro-i (Kanári-szigetek) kezdőmeridián használata, amely a
Greenwich-itől mintegy 17°40'-re Ny-ra fekszik. K-Európa több országában
Pulkovo-i kezdőmeridiánnal dolgoztak, amely Greenwich-től mintegy 30°20'-re
K-re helyezkedik el. A magyarországi térképezéseknél a gellérthegyi meridián
játszik fontos szerepet, amelynek a
ferroi kezdőmeridiántól való eltérését a Bessel-ellipszoidon
36°42'51.69"-nek tekintették, míg a greenwichi hosszúsága az IUGG'67-es
ellipszoidon 19°2'54.856"-nek van megállapítva.
Átszámítás derékszögű és földrajzi
koordináták között
A
forgási ellipszoid paraméteres alakját a
F földrajzi szélesség és
a L földrajzi hosszúság mint
paraméterek segítségével a
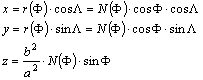
képletek
adják, amelyek a F, L földrajzi koordinátákkal
megadott pontok térbeli derékszögű koordinátáinak meghatározására szolgálnak.
Amennyiben a térbeli derékszögű koordinátákból kell a földrajzi koordinátákat
kiszámítani, akkor a z képletéből kifejezzük F-t:
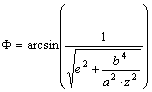
majd
az x
vagy az y képletéből a F segítségével L-t.
Vegyük
most a F, L földrajzi
koordinátákon kívül még az ellipszoid feletti
h magasságot is figyelembe. A
???ábráról leolvasható, hogy
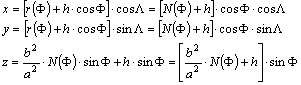
Ezekből
a képletekből tehát kiszámíthatók a
földrajzi koordinátákkal és az ellipszoid feletti h
magassággal megadott pont térbeli derékszögű koordinátái.
Az x, y, z
térbeli derékszögű koordináták
ismeretében először felírjuk az
![]()
összefüggést
és kifejezzük belőle h-t, amelyet a z
képletébe helyettesítünk. Az így kapott nem-lineáris összefüggésből a F egy negyedfokú egyenlet
megoldásán keresztül kapható meg. Az egzakt képlet, amelyet a műholdas
helymeghatározás használ fel, Borkowski-tól származik. Kevésbé pontos eredményt
adnak a földrajzi koordinátákra és a h
magasságra Bowring közelítő képletei:
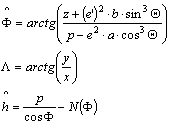
ahol
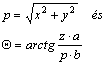
A
geodéziai felmérések során fontos szerepet kap az alapfelületen értelmezett forgásfelületi polárkoordinátarendszer. A
polártengely az O ponton áthaladó, az É-i irányt kijelölő meridiánív. A
polárkoordinátákkal (az OP geodetikus
vonal hosszával mint polártávolsággal és a 0° és 360° közé eső azimuttal mint
polárszöggel) adott P pont
földrajzi koordinátáinak kiszámítását első geodéziai alapfeladatnak nevezzük.
Ha a földrajzi koordinátákkal adott P
pont polárkoordinátáit számítjuk ki, akkor a második geodéziai alapfeladatot oldjuk meg. Gömb alapfelület esetén
mind az első, mind a második geodéziai alapfeladat gömbháromszögtani
összefüggésekkel oldható meg.
Segédföldrajzi koordináták
Gömb
alapfelület esetén értelmezhető a segédföldrajzi
koordinátarendszer. Ehhez először is ki kell jelölni a gömbön a segédpólust és ezzel együtt a
segédpoláris tengelyt. A segédpólustól egyenlő gömbi távolságra (segédpólustávolságra) lévő pontok
képezik a segédparallelköröket,
90°-os gömbi távolság esetén a segédegyenlítőt.
A segédpólustávolság pótszöge a j* segédszélesség. A két segédpólust összekötő gömbi főkörívek a segédmeridiánok. Ezek közül egyet segédkezdőmeridiánnak választva, ennek
félsíkja bármely segédmeridián félsíkjával a segédhosszúságnak nevezett l* szöget zárja be. A
segédhosszúságot a segéd-É-i pólus felől nézve az óramutató járásával
ellentétesen irányítjuk, és nagyságára: -180°£l*£180°. (Megjegyezzük, hogy az
esetek túlnyomó többségében a segédkezdőmeridián tartalmazza az egyik pólust,
ugyanis a pólusokon és a segédpólusokon áthaladó gömbi főkör - bimeridián -
egy-egy szakasza meridián és egyben segédmeridián is.) A segédföldrajzi
koordinátarendszer bevezetésének fő előnye abban áll, hogy segítségükkel
bizonyos rokonvetületek egységesen tárgyalhatók, és ezek leképezési függvényei
egyszerű, egységes alakban adhatók meg.
Tetszőleges
gömbfelületi (j,l) koordinátákkal megadott pont segédföldrajzi
(j*,l*) koordinátáinak
meghatározása a második geodéziai alapfeladatra vezethető vissza, míg a
segédföldrajzi (j*,l*) koordináták ismeretében az első geodéziai
alapfeladat megoldása alapján kapjuk a (j,l) földrajzi koordinátákat, mindkét esetben
gömbháromszögtani összefüggések segítségével.
A képfelület paraméterezése
A
képfelületet (az esetleges síkbafejtés után) paraméterezhetjük síkbeli derékszögű x,y koordinátarendszer
segítségével. Az egyik koordinátatengelynek célszerűen a fokhálózat
szimmetriatengelyét vagy egy azzal párhuzamos egyenest választjuk. Ennek
irányát szokás hálózati északi iránynak
is nevezni. A geodéziában előszeretettel tekintik a hálózati északi irányt x-nek, szemben a matematikában és a
vetülettanban inkább szokásos y-nal.
Derékszögű
koordinátarendszer alkalmazásakor a vetületi
egyenletek gömb alapfelület esetén, attól függően, hogy a j szélességet vagy a b pólustávolságot használjuk,
![]()
vagy
![]()
alakúak;
forgási ellipszoid alapfelület esetén (a F szélességgel vagy a B pólustávolsággal)
![]()
vagy
![]()
alakúak.
A parallelkörök
képei a vetületek egy részénél, különösen kúppalást-képfelületnél, körív
alakak. Ilyen esetben előnyös a képsíkon a polárkoordinátarendszer
bevezetése. A koordinátarendszer origója a körív középpontjába kerül, a
polártengely többnyire a középmeridiánnal esik egybe. (Nem-koncentrikus körívek
esetében az origó helyzete így a szélesség függvényében akár változhat is.)
Polárkoordinátarendszer
alkalmazásakor a leképezés függvényei gömb alapfelület esetén (r-val jelölve a
polártávolságot, g-val a polárszöget):
![]()
illetve
![]()
alakúak;
forgási ellipszoid alapfelület esetén
![]()
illetve
![]()
alakúak
A
képfelületi síkkoordinátarendszer origóját szokás vetületi kezdőpontnak nevezni.
Nevezetes alapfelületi vonalak és felületdarabok
Ortodrómák, gömbi és ellipszoidi körök,
loxodrómák
A
vetületek vizsgálatánál – a paramétervonalak mellett – az alapfelületi vonalak
három fajtája: az ortodrómának is
nevezett geodetikus vonal, a gömbi (ellipszoidfelületi) körív és a loxodróma játszik központi szerepet.
Az ortodróma tehát az alapfelületi pontokat
összekötő legrövidebb felületi görbeív. Gömb alapfelület esetén minden 180°-nál
nem nagyobb középponti szöghöz tartozó főkörív ortodróma, így a
(segéd-)meridiánok és a (segéd-)egyenlítő is. A meridiánokkal és az
egyenlítővel egybe nem eső gömbi főköröket szokás harántköröknek is nevezni. Az
ortodróma ívhosszát gömbön a radiánban megadott középponti szögnek az R sugárral való szorzata adja. A Dj szélességkülönséghez
tartozó meridiánív mint speciális ortodróma
s hossza így:
![]()
A
forgásfelületek (így a gömb- és a forgási ellipszoid-felületek) ortodrómáinak
fontos tulajdonságát fogalmazza meg a Clairaut-tétel. Eszerint a geodetikus
vonal és a forgásfelület parallelköre által bezárt szög (az azimut pótszöge) koszinuszának
és a parallelkör sugarának a szorzata – a geodetikus vonal mentén haladva – nem
változik. Jelölje a az azimutot a geodetikus
vonal tetszőleges pontjában, és r a
pontnak a forgástengelytől mért távolságát (másként a ponton áthaladó
parallelkör sugarát); ekkor Clairaut tétele képletben az alábbi alakot ölti:
![]()
A
minden parallelkört merőlegesen metsző felületi görbék – a meridiángörbék –
esetén ez a szorzat zérus, emiatt a meridiángörbék nyilván geodetikus vonalak.
(A forgási ellipszoidon az összes többi ortodróma térgörbe.) A F1 és F2 szélességek közötti
meridiánívhosszat az ellipszisív simulókör-sugarának (az M-mel jelölt meridiángörbületi sugárnak) a földrajzi szélesség
szerinti integráljaként kapjuk:
![]()
A parallelkörök mind gömbön, mind forgási ellipszoidon a poláris tengelyre nézve forgásszimmetrikus körök, amelyek gömb alapfelület esetén (az egyelítőt kivéve) gömbi kiskörök. E j szélességű parallelkörön egy Dl hosszúságkülönbséghez tartozó ív s hossza:
![]() .
.
A gömbfelületen a parallelkörökön kívül további felületi kiskörök is felvehetők. Egy ilyen kiskörön az ívhosszat – alkalmasan felvett segédföldrajzi koordinátarendszerben – az
![]()
képlet adja.
Forgási ellipszoid alapfelület F szélességű parallelkörén a DL hosszúságkülönbséghez tartozó s ívhossz:
![]()
Az egyenlítő, mint speciális a sugarú parallelkör mentén ez
![]() -vá egyszerűsödik.
-vá egyszerűsödik.
Loxodrómának azokat az alapfelületi vonalakat nevezzük, amelyeknek minden pontjában az a azimut állandó. A meridiánok az a=0° és a=180° azimuthoz tartozó speciális loxodrómák, a parallelkörök pedig az a=90° és a=270° azimuthoz tartozó speciális loxodrómák. A többi loxodróma olyan csavarvonal, amely az egyik pólusból a másik pólusba vezet. Írjuk fel gömb alapfelületre egy ilyen loxodróma egyenletét az egyértékűség miatt l=l(j) alakban. Ehhez változtassuk meg a j,l koordinátájú pontot Dj,Dl-val, ami egy kis foktrapézt hoz létre a gömbön, melynek oldalai arcDj és arcDl×cosj ; átellenes csúcsait kössük össze egy Ds hosszúságú loxodróma-ívvel (???ábra). A kicsiny foktrapéz oldalai és "átlója" közelítőleg síkban lévőnek tekinthetők, amelyben
![]() ; ezt egyszerűsítve és
átrendezve:
; ezt egyszerűsítve és
átrendezve: ![]()
Ha
most a loxodrómát kis darabokra bontjuk, akkor az összegzés, majd a minden
határon túli finomítás után az integrálás az alábbi eredményre vezet:
![]() ;
;
innen
![]()
Ha
a loxodróma pl. a j0,l0 koordinátájú ponton halad
át, akkor a C integrációs konstans:
![]()
Ekkor
a loxodróma egyenlete az alábbi alakban írható:
![]()
Egyenletünk
szerint minden j-hez egyetlen l tartozik, és j®±90° esetén l®±¥. Egy l-hoz viszont (a¹90° esetén) végtelen sok j is tartozhat.
A j1,l1 és j2,l2 koordinátájú pontokon áthaladó loxodróma azimutja:
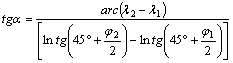
Az a azimuthoz tartozó loxodróma
j1 és j2 szélességek közé eső
darabjának ívhossza szintén az iménti ábra alapján adható meg, ugyanis:
![]() , ahonnan
, ahonnan ![]()
A
loxodróma-ívet kis részekre felosztva, a képletet az egyes részekre alkalmazva
összegzünk, ami a minden határon túli finomítás után integrálásba megy át:
![]()
innen
![]() .
.
vagyis a loxodróma-ív hossza az íven fellépő szélességmegváltozás lineáris függvénye.
Nevezetes alapfelületi
felületdarabok
Az alábbiakban megemlítünk néhány – alapfelületi vonalak által
határolt – nevezetes felületdarabot, amelyek a térképészetben szerepet
játszanak.
A térgeometriából ismert, hogy egy sík egy gömbfelületet két gömbsüvegre bont fel. Két párhuzamos
síkkal elmetszve a gömbfelületet, a két gömbsüveg között egy gömbövet kapunk. A j1 és j2 (j1£j2) szélességek
közé eső gömböv F felszíne:
![]()
(j1 =-90° vagy j2 =+90° esetén
ugyanez a képlet megadja az egy parallelkör által határolt gömbsüveg
felszínét.)
A forgási ellipszoidon az egyenlítő (F0 =0°) és F szélességi kör közé eső ellipszoid-öv F felszíne:
![]()
Ugyanez sor alakjában felírva:
![]()
A F -be 90°-ot
helyettesítve kapjuk a fél-ellipszoid felszínét, ennek kétszereséből pedig az Fe ellipszoidi
felszínt:
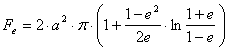
A fentiek alapján a F1 és F2 szélességi körök
közé eső ellipszoid-öv F felszíne:
![]()
illetve ugyanez sor-alakban:
![]()
Kössük össze a gömbfelület egyik átmérőjének végpontjait két gömbi
főkörívvel (félkörrel); ezek a gömbfelületet két gömbkétszögre bontják. A l1 és l2 meridián által
közrezárt gömbkétszög a teljes gömbfelszín (4×R2×p) arányos része,
F
felszíne tehát:
![]()
A forgási ellipszoidon is kijelölhető a határoló L1 és L2 meridiánokkal egy
ellipszoidi kétszög (zóna); ennek F
felszíne a forgási ellipszoid teljes felszínének arányos része:
![]()
A térképészetben jelentős szerepet játszik a j1 és j2 (j1£j2) parallelkör,
valamint a l1 és l2 (l1£l2) meridián által
határolt felületdarab, az ún. foktrapéz,
másként földrajzi négyszög. Ennek F
felszíne gömb alapfelületen:
![]()
Forgási ellipszoid alapfelületen a F1 és F2 (F1£F2) parallelkör,
valamint a L1 és L2 (L1£L2) meridián által
határolt foktrapéz felszíne:
![]()
A gömb alapfelületen végzett számítások fontos eszköze a gömbháromszög, amelyet három gömbi
főkörív határol. A gömbháromszögnek három oldala és három szöge van, amelyek
közül általános esetben három mennyiség független, a többi a gömbháromszögtani
tételek segítségével
kiszámolható. Ha a gömbháromszög szögeit a, b és g jelöli, akkor a gömbháromszög F felszíne:
![]() .
.
A
gömháromszög felszíne negatív nem lehet, így
a+b+g ³180°. Az e=a+b+g –180° mennyiséget gömbi szögfölöslegnek nevezzük. Ennek felhasználásával:
![]() .
.
Másrészt
a konvex gömbháromszög szögeinek összege 540°-nál kisebb.
A térképészeti számításokban gyakran használnak olyan
gömbháromszögeket, amelyeknek egyik csúcsa a pólusban van. Az ilyen
gömbháromszögeket szokás polárgömbháromszögnek
nevezni.
A síkháromszögek sok tulajdonsága a gömbháromszögekre is átvihető.
Így pl. két oldal összege nagyobb a harmadik oldalnál. A gömbháromszögben
nagyobb oldallal szemben nagyobb szög, egyenlő oldalakkal szemben egyenlő szög
helyezkedik el. Ezek alapján az általános gömbháromszögek mellett beszélhetünk
az egyenlő szárú (szimmetrikus) és az egyenlő oldalú (szabályos)
gömbháromszögekről.
A gömbháromszögekre vonatkozó tulajdonságok egy részénél előnyös,
ha egységsugarú gömbön vizsgáljuk ezeket. Ekkor a gömbháromszög oldalhosszai egyértelműen
megadhatók a hozzájuk tartozó középponti szögekkel. A továbbiakban tehát a gömbháromszög oldalait is szögekkel adjuk
meg. Az általános gömbháromszögek oldalai és szögei közül három tetszőleges
adat független, a többi adat az alábbi összefüggésekkel határozható meg.
A gömbháromszög szögeire (a,b,g), valamint a
velük szemközti oldalakra (a,b,c) vonatkozik
az ún. gömbháromszögtani szinusztétel:
![]()
A
gömbháromszög oldalai és egyik szöge között teremti meg a kapcsolatot az ún. gömbháromszögtani oldal-koszinusztétel, pl. az a oldalra és a vele szemközti a szögre felírva:
![]()
A
gömbháromszög szögei és egyik oldala közötti összefüggést az ún. gömbháromszögtani szög-koszinusztétel adja meg, pl. az a oldalra és a vele szemközti a szögre felírva:
![]()
Ha adott a három oldal, vagy két oldal és a közbezárt szög, akkor
az oldal-koszinusztétellel; ha a három szög, vagy egy oldal és a rajta fekvő
két szög, akkor a szög-koszinusztétellel lehet elindulni a megoldásban.
A fenti tételek kombinálásával minden ismeretlen adat
kiszámítható, de gyakran jól hasznosítható az ún. második alapforma is, amely két oldal, a közbezárt szög és
valamelyik másik szög között létesít összefüggést:
![]()
(A baloldalon szereplő oldalak kiválasztása és sorrendje szerint
összesen 6 alakja írható fel.) Mint látható, az a oldal és az a szög ebből
kifejezhető, azonban a b oldal és a g szög kiszámítása másodfokú egyenletre vezet.
Meridiánkonvergencia az alapfelületen és a
térképen
A
meridiánok a pólus felé összetartanak, ezzel kapcsolatos a meridiánkonvergencia fogalma, amely mind a térképészetben, mind a
navigációban használatos.
A
meridiánok összetartásának mértékét fejezi ki az alapfelületi meridiánkonvergencia. Vegyünk két pontot (P1 és P2) az alapfelületen és kössük össze ezeket egymással és
a pólussal ortodrómaívek segítségével. A két pontbeli azimut különbségének 180°
feletti részét nevezzük a (c-vel jelölt) alapfelületi
meridiánkonvergenciának. Képletben:
![]()
Gömb
alapfelület esetén egyszerű összefüggés adható meg a gömbi szögfölösleg és a
valódi gömbi meridiánkonvergencia között. Ehhez írjuk fel a P1, a P2 és a pólus által meghatározott polárgömbháromszög
belső szögeinek összegét (???ábra):
![]()
ahol
Dl a két pont
hosszúságkülönbsége és e a gömbi szögfölösleg.
Átrendezve az egyenletet:
![]()
vagyis
![]() .
.
A
navigációban az alapfelületi meridiánkonvergencia kiszámítására az alábbi
közelítő képletet használják:
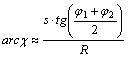
ahol arcc a
meridiánkonvergencia ívmértéke, s
jelöli a P1 és P2
pontok közötti távolságot (km-ben), j1 és j2 a
pontok szélességét, R pedig a közelítő
földsugarat (R=6371.1km).
A vetületi meridiánkonvergencia az a m -vel jelölt szög (???ábra),
amelyet a képfelületi P' ponton
áthaladó meridiánkép érintője a képfelületi derékszögű koordinátarendszer
hálózati északi irányt kijelölő tengelyével bezár, és amelyet az óramutató
járásával ellentétesen irányítunk. A vetületi meridiánkonvergenciának a
vetületek geodéziai alkalmazásánál van szerepe.