Átszámítások különböző alapfelületek koordinátái között

A különböző időpontokban, különböző körülmények között rögzített pontok földi koordinátái különböző alapfelületekre (ellipszoidokra geodéziai dátumokra) vonatkoznak. Ha ezeket a koordinátákat együttesen akarjuk felhasználni, akkor szükséges, hogy valamilyen közös vonatkoztatási rendszerbe legyenek összehozva. Ez általában a koordinátáknak az egyik ellipszoidról a másikra ill. az egyik geodéziai dátumról a másikra való átszámolását igényli.

Más esetben az ellipszoidfelületet (vagy annak egy részét) gömbfelülettel közelítjük. Ilyenkor az ellipszoidfelületi pontok koordinátáit kell valamilyen gömbfelületi koordinátáka átszámítani, vagy megfordítva. Az ilyen átszámításokat gömbvetületeknek nevezik.

Átszámítások különböző geodéziai dátumok koordinátái között

A pontok földrajzi koordinátái – közvetve vagy közvetlenül – geodéziai mérésekből erednek. A mérési hibák miatt a különböző geodéziai dátumok között egzakt átszámítás általában nem lehetséges. A közelítő átszámításhoz többféle módszert fejlesztettek ki.

Molodenski 3 paraméteres transzformációja

A transzformáció párhuzamosnak tekinti a kiindulási és a céldátum forgástengelyét, és az origó eltolásával viszi át az egyik ellipszoidot a másikba. (Az eltolás paraméterei térbeli derékszögű koordinátákban: DX, DY és DZ.) Figyelembe veszi továbbá a két ellipszoid méretének eltérését: a nagytengelyek Da különbségét, valamint a lapultságok Df különbségét. Az egyszerűsített transzformáció képletei úgy vannak megadva, hogy az eltoláshoz ne kelljen a földrajzi koordináták (+ tszf. magasság) és a térbeli derékszögű koordináták között oda- és visszaalakítást végezni, tehát a képletek közvetlenül a földrajzi koordinátákra elvégezhetők legyenek.

Egy adott területen elhelyezkedő pontok transzformálásához illesztőpontokra van szükség, melyeknek mindkét rendszerbeli koordinátáit ismerjük. Ezekből az illesztőpontokból számítható ki az adott területre közelítőleg jellemző DX, DY és DZ paraméter.

Transzformáció térbeli derékszögű koordináták között 7 paraméterrel

A térbeli pontok Helmert-transzformációja egy eltolás, egy hasonlósági transzformáció és három elforgatás együttes alkalmazását jelenti. A 7 paraméter: az eltolásvektor 3 komponense (DX, DY és DZ), az x, y és z koordinátatengely körüli elforgatások (e_x, e_y és e_z), továbbá a hasonlósági transzformáció (1+k) aránya. Feltételezve, hogy a koordinátatengely körüli elforgatások igen kis szöggel történnek, az (X, Y, Z) térbeli ponthoz a transzformált (X’, Y’, Z’) koordinátákat az alábbi képlettel rendeljük hozzá:

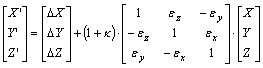
Ha a kiindulási pontunk földrajzi koordinátáival (és magasságával) van megadva, akkor ezeket először át kell számítani térbeli derékszögű koordinátákká. Ezeken végrehajtva a transzformációt, az ebből kapott derékszögű koordinátákat Bowring vagy Borkowski képletével visszaalakítjuk földrajzi koordinátákká (és magassággá).

E transzformációt a térinformatikában Bursa-Wolff transzformációnak nevezik.

Egy adott területen elhelyezkedő pontok transzformálása itt is (mindkét rendszerben ismert koordinátájú) illesztőpontokat igényel. Az eltolási, elforgatási és nagyítás-kicsinyítési paraméterek az illesztőpontok segítségével, közelítő számítással kaphatók meg, amelyek az illesztőpontok környezetében használhatók.

Átszámítások az ellipszoidi és gömbi koordináták között – a gömbvetületek

Gömbvetületnek nevezzük azokat a speciális leképezéseket, amelyeknek alapfelülete forgási ellipszoid, képfelülete pedig gömb. A gömbvetületektől elvárjuk, hogy a parallelkörök képe parallelkör, a meridiánok képe meridiánok legyen, valamint a parallelkörök képei legyenek ekvidisztánsak: tehát j=j (F) és l=n×L (n=const).

Írjuk fel a gömbvetületek fokhálózat menti hossztorzulásait. Jelöljük a megfelelő DL és Dl hosszúságkülönbségekhez tartozó parallelkör menti ívhosszakat Dp-vel és Dp’-vel, a megfelelő DF és Dj szélességkülönbségekhez tartozó meridián menti ívhosszakat Dm-mel és Dm’-vel. Ekkor a

parallelkör menti h hossztorzulás:

;

a meridián menti k hossztorzulás:

A fokhálózati vonalak mind a forgási ellipszoidon, mind a gömbön merőlegesen metszik egymást, ezért a többi torzulás visszavezethető a fokhálózat menti hossztorzulásokra.

Amennyiben a gömbvetületeket a geokartográfiában használják, akkor általában megkövetelik, hogy a teljes forgási ellipszoid pontosan a teljes gömbre képeződjön le (ez az n=1 feltételt jelenti), továbbá hogy az ellipszoidi egyenlítő képe a gömbi egyenlítőre essen (vagyis F=0 esetén j=0 legyen).

Területtartó gömbvetület:

A területtartás alapegyenlete: h·k=1 azaz

A differenciálegyenlet megoldása:

Alakítsuk át a jobb oldalon álló integrandust:

Ennek alapján elvégezve az integrálást:

Fejezzük ki innen j -t:

Ezt a vetületet többnyire geokartográfiai célokra használják, ezért a fentiek miatt n=1, továbbá a F=0 esetén elvárt j=0 egyenlőségből következik k=0. Hátra van még R meghatározása. A területtartásnak a teljes gömbfelszínre is fent kell állnia, tehát

ahonnan R kifejezhető:

Meridiánban hossztartó gömbvetület

A meridiánban hossztartás alapegyenlete:

A differenciálegyenlet megoldása: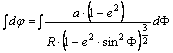

Elvégezve az integrálást: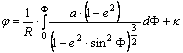

F=0 esetén itt is elvárjuk, hogy legyen j=0, innen következik k=0.

A hossztartásnak a teljes meridiánra is fenn kell állnia, ezért j=p/2 -hez F=p/2 tartozik.

Átrendezve az egyenletet kapjuk R-et: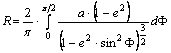

Szögtartó gömbvetület:

A szögtartás alapegyenlete: h=k , azaz

A differenciálegyenlet megoldása:

Alakítsuk át az integrandust a jobboldalon:

Ennek segítségével végezzük el az integrálást:

Mindkét oldalt felemelve e alapra:

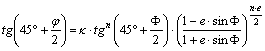
Ebből a j felírható explicit alakban:

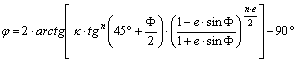
A F azonban nem fejezhető ki. Ezért abban az esetben, ha adott j -ből kell F értékét kiszámítani, az alábbi közelítés ajánlható:

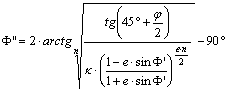
(A jobboldali kifejezésbe F’ helyére egy közelítő értéket helyettesítve, a képlet a F-nek egy jobb F” közelítését adja. Ezt addig folytatjuk, míg a két közelítés eltérése egy előre megadott pontossági korlátot, pl. 0.0001”-et meghaladja. Kezdőértéknek választható pl. F’=j .)

Ha a vetületet geokartográfiai célokra akarjuk használni, akkor itt is n=1, továbbá elvárjuk, hogy F=0° esetén j=0° legyen. Ezt a fenti képletbe helyettesítve kapjuk, hogy k=1.

Az R meghatározásához írjunk elő egy hossztartó parallelkört, melynek ellipszoidi szélessége F_n, gömbi szélessége j_n. (A két hossztartó szélesség általában nem egyezik meg!) A hossztartás képletben:

,

és innen R kifejezhető.

Ha a vetületet topokartográfiai célokra akarjuk használni, akkor további követelményeket kell szabni n és k meghatározására:

- legyen egy j_n ill. F_n szélességekkel adott hossztorzulásmentes (normál)parallelkör;

- legyen az l hossztorzulási modulus logaritmusa (ln l) harmadrendű mennyiség (vagyis a j_n körüli sorfejtésében csak a harmad- és magasabbrendű tagok térhetnek el 0-tól).

E követelményekből kiindulva Gauss az alábbi összefüggéseket vezette le:

Adott forgási ellipszoid esetén ez az egyenletrendszer 4 ismeretlent (n, j_n , F_n és R) tartalmaz, amelyek közül bármelyiket megadva, a többi következik az egyenletrendszer megoldásából. A konstansok meghatározása a hossztartó parallelkör ellipszoidi vagy gömbi szélességének kijelölésével kezdődik. A második összefüggésből mind j_n –et, mind F_n -et ki lehet fejezni. Ha az ellipszoidi szélesség adott, akkor a

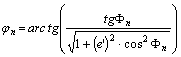képletet,

ha a gömbi szélességből indulunk ki, akkor a

képletet használjuk. A következő lépésben az első képletből kifejezzük n-et:

F_n ismeretében az utolsó egyenlet közvetlenül adja R-et, az ún. simulógömb sugarát:

Végül a

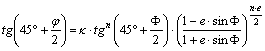
összefüggésbe behelyettesítve n, j_n és F_n értékeit, kiszámítható k.

Ez a leképezés a Gauss-féle kis hossztorzulású szögtartó gömbvetület, melyet a magyarországi felméréseknél 1857 óta alkalmaznak a Bessel ellipszoid alapfelületre,

j_n =46°30’, illetve 1975 óta az IUGG’67 ellipszoidra a F_n=47°10’ választással. Ennél a két leképezésnél a második irányredukció 50 km-es hossznál nem haladja meg a 0.008”-et, ezért a háromszögelésnél figyelmen kívül hagyható. A lineármodulus maximális eltérése az egységtől Magyarország területén kb. 1/4000000.