A ferdetengelyű szögtartó hengervetület és magyarországi alkalmazásai

Perspektív hengervetületek

A perspektív hengervetületek a gömb alapfelületet egy forgáshenger palástjára képezik le középpontos geometriai vetítéssel. A vetítés Q középpontja szimmetria okokból a hengerpalást forgástengelyén helyezkedik el. Az alapfelületi P pont képe a QP vetítősugárnak a hengerpalásttal alkotott P’ döféspontja lesz (???ábra).

Essen egybe a gömb forgástengelye a hengerpalát-képfelület forgástengelyével – ez az ún. normális vagy poláris helyzet. Ha a P pont egy parallelkörön megy körbe, akkor a rajta áthaladó vetítősugarak egy forgáskúp palástját írják le, amelynek forgástengelye egybeesik a képfelület forgástengelyével, így azt egy – a forgástengelyre merőleges – körben metszi. A parallelkörök képei ezért a hengerpalást alkotóira merőleges körök lesznek. Ha a P pont egy meridiánon halad végig, akkor a vetítősugarak a meridián (mint gömbi főkör) síkjában maradnak, ezért a meridián e síknak a képfelülettel alkotott metszésvonalára, a hengerpalást egyik alkotójára képeződik le. A hengerpalástot az egyik alkotója mentén felvágva és síkba kiterítve, a meridián-képek párhuzamos egyenesek lesznek, a parallelkörök képei pedig ezekre merőleges, egymással párhuzamos egyenes-seregbe mennek át. A térképi síkkoordináta-rendszer y tengelye essen egybe az egyenlítő képével, az x tengely pedig a kezdőmeridián képével. A fokhálózati vonalak párhuzamossága miatt a vetületi egyenletek csak egy-egy koordinátától függnek:

A parallelkör-képeket a meridián-képek a meridiánok által bezárt szögek arányában metszik, emiatt y lineáris függvénye l-nak:

A térképi fokhálózat ortogonalitása miatt a fokhálózati vonalak itt is vetületi főirányok, amelyek irányában fellépő hossztorzulások megegyeznek az a maximális és a b minimális hossztorzulással. A fokhálózat menti hossztorzulások az ???ábra alapján, az y vetületi egyenlet linearitása figyelembevételével számíthatók ki:

A c együtthatót a hossztartó parallelkör j_n szélessége alapján határozzuk meg. Ha az egyenlítő hossztartó, akkor

, vagyis c=1, tehát .

Ha van két (±j_n szélességű) hossztartó parallelkör, akkor

, vagyis c=cosj_n; ekkor .

Végül a hossztartó szélesség nélküli („külső elhelyezésű”) vetületektől gyakorlati okokból itt eltekintünk.

A meridián menti k hossztorzulás:

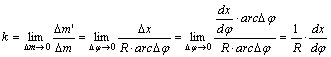
A szögtartó hengervetület

Rendelkezzen egy vetület a fentiekben leírt fokhálózati tulajdonságokkal, függetlenül attól, hogy előállítható-e centrális geometriai vetítéssel vagy sem. Ez azt jelenti (ÉK-i tájékozás mellett), hogy a leképezést az

vetületi egyenletekkel valósítjuk meg, ahol a szokásos követelmények mellett az x a j-nek páratlan függvénye (emiatt az y tengely az egyenlítő képével esik egybe). A vetület akkor lesz szögtartó, ha a fokhálózat irányaiban mint vetületi főirányokban fennáll a hossztorzulások egyenlősége:

vagyis

.

Oldjuk meg az egyenletet és végezzük el az integrálást:

ahol j=0 esetén x=0 akkor teljesül, ha a d=0. Tehát

Ez átalakítható a már ismert módon:

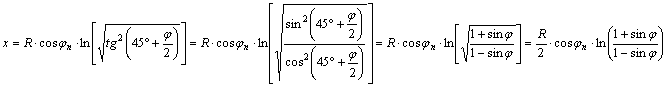A szögtartó hengervetület inverz vetületi egyenletei:

E vetületben a teljes Föld nem ábrázolható, a gyakorlatban a j=±70-75°-on túli területet az ábrázolásból elhagyják. A szögtartó hengervetület egyenlítőben hossztartó változata a XVI. század óta ismert Mercator-vetület. A fokhálózat menti hossztorzulások a j szélesség függvényében a ???ábrán láthatók, mely szerint a hossz- (és terület) torzulások a torzulásmentes egyenlítőtől távolodva eleinte fokozatosan, majd gyorsulva növekednek. A ±60°-os szélességen a hossztorzulás 2-szeres, a területtorzulás 4-szeres. A topokartográfiában kedvezőtlennek tartott hossztorzulások 1.0001-es alsó határa az

egyenletből következik:

.

Eszerint a Mercator-vetület az egyenlítő körüli, a ±0.81025°-os szélességek közé eső, 180.2 km szélességű sávban felel meg a topokartográfia szigorú torzulási követelményének.

A szögtartó hengervetület ±j_n szélességeken hossztartó változatában a fokhálózat menti hossztorzulások j szélességtől való függését a ???ábra mutatja. Az egyenlítőtől a j_n hossztartó szélességig a hosszak csökkennek, onnan a pólusok felé egyre gyorsulva növekednek. Az a sáv, amelyen belül a hossztorzulásoknak 1-től való eltérése kisebb, mint 0.0001, szélesebb, mint a Mercator-vetületnél.

A szögtartó hengervetület fontos tulajdonsága, hogy a loxodrómák a térképen egyenesekre képeződnek le. Ez évszázadokon keresztül nagy jelentőséggel bírt a geokartográfiában; a tengeri navigáció térképei nagyrészt Mercator vetületben készültek.

A ferdetengelyű szögtartó hengervetület

A szögtartó hengervetület ugyan nem perspektív, de itt is definiálható a ferdetengelyű helyzet. Vegyünk fel ehhez az N*(j₀, l₀) segédpólus segítségével egy segédföldrajzi koordinátarendszert (???ábra), és vonatkoztassuk erre a vetületi egyenleteket:

majd ezeket az ismert gömbháromszögtani összefüggésekkel átalakítjuk j és l függvényévé. Az oldal-cosinus-tételből:

Innen

Továbbá

és

Az y vetületi egyenlet attól függően, hogy melyik összefüggést használjuk:

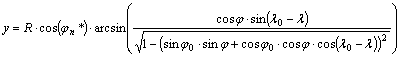
vagy

Ezekben az egyenletekben az ábrázolandó területen kívül fekvő segédpólus j₀, l₀ koordinátái szerepelnek. Előnyösebb, ha a segédegyenlítő és a kezdő-segédmeridián metszéspontjában felvesszük a K(j_K, l_K) vetületi kezdőpontot, és ennek koordinátáival fejezzük ki a vetületi egyenleteket (figyelembe véve, hogy j_K=90°-j₀ és a l_K=l₀ ±180°):

és

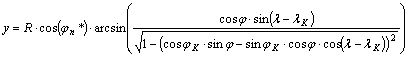
vagy

Az inverz vetületi egyenletek közvetlenül a segédföldrajzi koordinátákra írhatók fel:

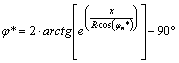
Ezekből a

és a

egyenletek adják a gömbi földrajzi koordinátákat.

Meghatározhatók az inverz vetületi egyenletek közvetlenül a síkkoordinátákból is. Ehhez vezessük be a

és a

jelölést. A vetületi egyenletek átrendezésével kapjuk, hogy

és

.

Az első egyenletből fejezzük ki cos(l–l_K) –t:

Ezt helyettesítsük vissza a második egyenletbe, majd abból fejezzük ki sin(l–l_K) –t:

.

Másrészt ez az egyenlőség felírható a

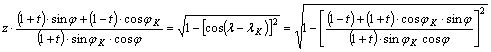
alakban. Négyzetreemelés és közös nevezőre hozás után:

Ez sinj -ben másodfokú egyenlet:

Ennek megoldása sinj -re:

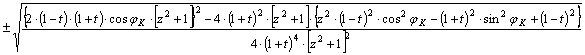
Az egyszerűsítések elvégzése után:

A képletben szereplő második tag a l_K hosszúsághoz mint középmeridiánhoz tartozó félteke azon pontjaira, amelyek a K vetületi kezdőponttól 90°-nál kisebb gömbi távolságra vannak, + előjellel, a félteke többi pontjára – előjellel veendő figyelembe.

Ha sinj már megvan, akkor sin(l–l_K) és cos(l–l_K) a fenti képletekkel kiszámítható. Visszahelyettesítve sinj -t a sin(l–l_K) képletébe kapjuk, hogy

,

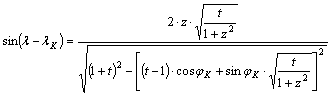amely a (l–l_K) hosszúságkülönbséget a l_K hosszúsághoz mint középmeridiánhoz tartozó félteke azon pontjaira adja meg, amelyek a K vetületi kezdőponttól 90°-nál kisebb gömbi távolságra vannak.

A ferdetengelyű szögtartó hengervetület magyarországi alkalmazása

A ferdetengelyű szögtartó hengervetületet 1908-ban vezették be a magyarországi topokartográfiában. A kettős leképezés alapfelülete továbbra is a Bessel-ellipszoid volt, amelyen azonban – a háromszögelési rendszer újratájékozása eredményeként – a sztereografikus rendszerből ismert pontok koordinátái kissé megváltoztak. Az ellipszoidi koordinátákat a Gauss-féle szögtartó gömbvetülettel képezték le a Gauss-simulógömbre. A gömb és a leképezés paraméterei megegyeztek a sztereografikus vetületnél használtakkal.

A gömbi koordinátákból ferdetengelyű szögtartó hengervetülettel képeztek le síkra. A korabeli országterülethez igazodva három hengervetületet vettek fel: egy É-i (Hengervetületi Északi Rendszer, röviden HÉR), egy középső (Hengervetületi Középső Rendszer, röviden HKR) és egy D-i sávot (Hengervetületi Déli Rendszer, röviden HDR). Mindhárom hengervetület vetületi kezdőpontja a gellérthegyi kezdőmeridiánon (l_K=0.0°) volt, az alábbi gömbi szélességeken:

a HÉR-ben j_K=48° 40’ 2.0”;

a HKR-ben j_K=47° 06’ 0.0”;

a HDR-ben j_K=45° 31’ 59.0”.

A gellérthegyi meridiánt e pontokban merőlegesen metsző harántkörök (a segédegyenlítők) torzulásmentesek, innen É és D felé haladva a hossztorzulások (valamint a területtorzulások) nőnek, és a segédegyenlítőtől mintegy 90 km távolságban érik el az 1.0001 értéket. Ez csak kisebb területeket érintett a történelmi Magyarország déli és északi határvidékén.

Mind a három rendszer DNy-i tájékozású, és segédegyenlítőben hossztartó, emiatt cosj_K*=1. A vetületi egyenletek tehát:

és

ahol l a gellérthegyi hosszúságot jelenti.

A hengervetületi rendszerben készült térképeket kataszteri térképekhez használták. Szelvényezése – szemben a sztereografikus vetületben készült térképekével – a síkkoordináta-hálózat mentén történt, ezért az egyes szelvények pontosan téglalap alakúak. Megalkotása Fasching Antal nevéhez fűződik.

Az Egységes Országos Vetület (EOV)

Hazánkban az 1970-es évek elején polgári célokra új topográfiai és kataszteri térképrendszert (Egységes Országos Térképrendszer, rövidítve EOTR) vezettek be, amelyhez új háromszögelési hálózatot hoztak létre. Az új térképrendszer új vetületben (Egységes Országos Vetület, rövidítve EOV) készült, melynek használata 1975-től vált kötelezővé.

Az EOV tekinthető a HKR korszerűsített változatának. A kettős leképezés alapfelületéül a műholdas mérésekből levezetett és a Nemzetközi Geodéziai és Geofizikai Unió (IUGG) által elfogadott ún. IUGG’67 ellipszoidot, illetve az ezen alapuló HD72 geodéziai dátumot választották, amelyről első lépésben a Gauss-féle szögtartó gömbvetülettel képeztek le az új Gauss-simulógömbre (R=6379743 m). A leképezés paraméterei:

n= 1.000 719 704 936

k= 1.003 110 007 693

Szükséges még a számolásokhoz az IUGG’67-ellipszoid első excentricitása:

e= 0.081 820 567 9407

A második lépésben a gömbi koordinátákból egy ferdetengelyű, redukált szögtartó hengervetülettel tértek át a síkra. A vetületi kezdőpont itt is a gellérthegyi meridiánra esik, koordinátái: j_K=47°06’0.0”; l_K=0.0°. A koordinátarendszer ÉK-i tájékozású. A vetületi egyenletek egy-egy eltolást is tartalmaznak (az x tengely irányában 200 000m, az y tengely irányában 650 000m):

Az eltolások következtében a koordináták mindig pozitívak, továbbá az x koordináták 400 000m-nél mind kisebbek, az y koordináták pedig 400 000m-nél mind nagyobbak. A vetületi egyenletek tartalmazzák még a cosj_n*=0.99993 értékű redukciós tényezőt, amelynek hatására az ország területén fellépő maximális hossztorzulás a HKR-énél előnyösebb. A vetületi kezdőponton áthaladó, a gellérthegyi meridiánra merőleges harántkör (a segédegyenlítő) körüli mintegy 150 km széles sávban a hosszak és a területek csökkennek; a j_n*=±0.6779367° segédparallelkörökön a vetület torzulásmentes; ettől távolodva a hossz- és területtorzulások növekednek. (A legnagyobb hossztorzulás az ország É-i határvidékén lép fel, értéke az 1.00025-öt csak kevéssel haladja meg.)

Az inverz vetületi egyenletek:

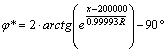
és

;

a j*, l* segédkoordinátákból a gömbi földrajzi koordináták a

és a

egyenletekkel számíthatók ki.

Az EOTR szelvényhatárai szintén a síkkoordinátahálózathoz igazodnak, emiatt az egyes szelvények itt is téglalap alakúak.

Egyéb ellipszoid alapfelületű ferdetengelyű szögtartó hengervetületek

Rosenmund svájci térképész használta először az ellipszoid alapfelületű ferdetengelyű szögtartó hengervetületet Svájc topográfiai térképezéséhez (1903). 1928-ban Laborde francia geodéta Madagaszkár topográfiai célú ábrázolásához konstruált hasonló vetületet. Az ellipszoidról közvetlenül síkra képező vetület képleteit ma Hotine brit geodéta (1946) számításai alapján használják, mellette Cole brit és Thomas amerikai geodéta is foglalkozott ezzel a vetülettel.