A KOORDINÁTARENDSZEREK FOGALMA. SÍKBELI, TÉRBELI ÉS FELÜLETI POLÁRKOORDINÁTARENDSZEREK

Koordináta és koordinátarendszer fogalma

Koordinátának olyan számokat nevezünk, amelyek ponthalmazok esetén egyértelműen megmondják, hogy a halmaz melyik pontjáról van szó; általában a pontok helyzetének megadásával teszik azonosíthatóvá a pontokat. Azt az előírást, amely a ponthoz a koordinátákat hozzárendeli, koordinátarendszernek nevezzük. A műszaki létesítmények, a földtudományi kutatásokhoz létesített objektumok földrajzi (térbeli) helyzetének pontos rögzítése során, a geodéziai felmérés és a térképkészítés folyamatában nagy mennyiségű pont azonosítása válik szükségessé, ezért itt a koordinátarendszerek vizsgálatának kitüntetett szerepe van.

Síkbeli pontok jellemzése koordinátákkal

Síkbeli derékszögű koordináták

Síkbeli pontokat leggyakrabban derékszögű (ortogonális) koordinátákkal jellemeznek, ami az origóból a P ponthoz vezető helyvektor merőleges összetevőkre való egyértelmű felbontásán alapul. Jelöljön i és j egymásra merőleges két egységvektort. Ekkor a P pont helyvektorának

alakú előállításából származó x, y skalárokat a P pont derékszögű koordinátáinak nevezzük. Az origón áthaladó, i és j irányú irányított egyenesek a szokásos módon x,y-nal jelölt koordinátatengelyek. A matematikában az x-tengelyt általában pozitív (az óramutató járásával ellentétes irányú) 90°-os elforgatás viszi át az y-tengelybe, ezzel szemben a geodéziában többnyire a negatív irányú 90°-os elforgatás az elfogadott. A térképlapon a derékszögű koordináták növekedhetnek felfelé és jobbra („ÉK-i tájékozás”), vagy – ritkábban – lefelé és balra („DNy-i tájékozás”).

A derékszögű koordinátarendszerek egyszerű transzformációi: az eltolás, az origó körüli elforgatás, és az x vagy y irányú merőleges affinitás. Jelölje az x,y koordinátájú pont transzformáció utáni koordinátáit x’,y’. Ekkor a koordinátarendszer origójának x₀,y₀ pontba való eltolását az

képletek; a koordinátarendszer origó körüli, az óramutató járásával ellentétes irányú d szöggel való elforgatását a

képletek; végül az x irányú (y tengelyre merőleges) c_x-szeres affinitást az

képletek, míg az y irányú (x tengelyre merőleges) c_y-szoros affinitást az

képletek adják meg. A fentiekben felsorolt transzformációkat kombinálni is lehet, de ebben az esetben ügyelni kell a transzformációk végrehajtásának sorrendjére.

Síkbeli polárkoordináták

A síkbeli pontok jellemezhetők polárkoordinátákkal is. Az origóból kiinduló félegyenes a polártengely; a P pont origótól mért r távolságát polártávolságnak vagy polársugárnak, az OP vektor polártengellyel bezárt (konvex) b szögét polárszögnek nevezzük. A b polárszöget többnyire az óramutató járásával ellentétes irányban tekintjük pozitívnak, de ellenkező irányítás is előfordul.

A polárkoordináták és a derékszögű koordináták közötti átszámítást – amennyiben a polártengely pl. a derékszögű koordinátarendszere x tengelyének pozitív felével esik egybe, és a skálázás az egybeeső tengelyeken megegyezik – az

és az

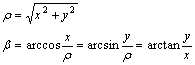
képletek adják meg. (b pontos értékéhez figyelembe kell venni a trigonometrikus függvények inverzeinek többértékűségét.) Általános helyzetű koordinátarendszerek esetén a fenti helyzet létrehozásához előbb egy transzformációt kell végrehajtani, amely egy eltolásból, egy elforgatásból, valamint egy x és/vagy y irányú merőleges affinitásból tevődik össze.

Térbeli pontok jellemzése koordinátákkal

Térbeli derékszögű koordináták

A térbeli pontok jellemzése – a síkbeli pontok jellemzésének analógiájára – kézenfekvő módon lehetséges derékszögű (ortogonális) koordinátákkal. Jelölje i, j és k az egymásra kölcsönösen merőleges egységvektorokat, amelyek jobbrendszert alkotnak. A P pont helyvektora egyértelműen előállítható

alakban; az x, y, z skalárokat a P pont (térbeli) derékszögű koordinátáinak nevezzük.

A térbeli derékszögű koordinátarendszerek transzformációi hasonlóak a síkbeli koordinátarendszerekéhez. Az origó x₀,y₀,z₀ pontba való eltolását az

képletek adják meg. Az (óramutató járásával ellentétesen irányított) elforgatás alapesetei: az x koordinátatengely körüli d szögű elforgatás az

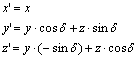
képletekkel; az y koordinátatengely körüli d szögű elforgatás a

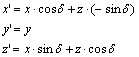
képletekkel; a z koordinátatengely körüli d szögű elforgatás az

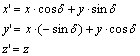
képletekkel történik. Ezen elemi elforgatások egymás utáni alkalmazásából bonyolultabb elforgatások építhetők fel, amelyek eredményét az elforgatások szögein kívül azok sorrendje is befolyásolja.

Az x irányú (yz síkra merőleges) c_x-szeres affinitást az

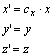
képletek; az y irányú (xz síkra merőleges) c_y-szoros affinitást az

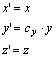
képletek; végül a z irányú (xy síkra merőleges) c_z-szeres affinitást az

képletek adják meg.

Az eltolási, elforgatási és merőleges affinitási transzformációk egymás utáni alkalmazásánál szintén figyelni kell a végrehajtás sorrendjére.

Térbeli polárkoordináták

A térbeli polárkoordináták értelmezése némileg hasonló a síkbeli polárkoordinátákéhoz. A koordinátarendszer polártengelye legyen az origóból kiinduló félegyenes, és legyen adott egy kezdő félsík, amely a határán tartalmazza a polártengelyt. Tetszőleges P pont polártávolsága az OP vektor r hossza; egy másik koordinátát az OP vektor polártengellyel bezárt (konvex) b szögéből kapjuk; végül a harmadik koordináta a kezdő félsík és a vele közös határú, P pontot tartalmazó félsík által bezárt (előjeles) l szög alkotja.

A térbeli derékszögű koordináták és polárkoordináták közötti átszámításhoz tételezzük fel, hogy a polártengely a derékszögű koordinátarendszere z tengelyének pozitív felével esik egybe, és a skálázás az egybeeső tengelyeken megegyezik. Ekkor az átszámítást az

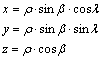
illetve a

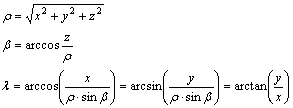
képletek adják meg. (l pontos értékéhez figyelembe kell venni a trigonometrikus függvények inverzeinek többértékűségét.) Általános helyzetű koordinátarendszerek esetén a fenti helyzet létrehozásához előbb egy transzformációt kell végrehajtani, amely egy eltolásból, egy vagy több elforgatásból, valamint egy x,y és/vagy z irányú merőleges affinitásból tevődik össze.

Forgásfelület pontjainak jellemzése felületi polárkoordinátarendszerrel

A polárkoordinátarendszer általánosítását tetszőleges forgásfelületen is értelmezhetjük. Forgásfelülethez úgy jutunk, hogy egy síkgörbét elforgatunk egy egyenes mint forgástengely körül. A forgásfelületet a forgástengelyre illeszkedő síkkal elmetszve ún. meridiángörbét kapunk.

Polártengelynek az origóból kiinduló meridiángörbét tekintjük. A polártávolság a vizsgált P pontot és az origót összekötő legrövidebb felületi görbeív (az ún. geodetikus vonal) hossza; a polárszög, amelyet itt azimutnak nevezünk, a polártengely iránya és az origóból a P pont felé induló geodéziai vonal érintője által bezárt szög, és amelyet az óramutató járásával megegyezően irányítunk (???ábra).