A sztereografikus
vetület és magyarországi alkalmazása
Perspektív síkvetületek
A perspektív síkvetületek a gömb alapfelületet síkra képezik
le középpontos geometriai vetítéssel. A vetítés Q középpontja szimmetria okokból a
gömbközépponton átmenő, a képsíkra merőleges egyenesen (a képsík
forgástengelyén, az ún. vetítési fősugáron)
helyezkedik el. Jelöljük a Q vetítési középpont és az O gömbközéppont távolságát f-fel, a vetítési középpont és a
képsík távolságát c-vel (???ábra). (Az f távolságot abban a
–
gyakorlatilag figyelmen kívül hagyható – esetben negatívnak tekintjük, ha a Q
vetítési középpont a képsík és a gömbközéppont között helyezkedik el.) Ekkor az
alapfelületi P pont képe a QP vetítősugár P’ döféspontja lesz a képsíkon. A
vetítési fősugárnak a K döféspontját a képsíkon vetületi kezdőpontnak nevezzük.
A perspektív síkvetület tulajdonságait lényegében az szabja
meg, hogy milyen a vetítési középpontnak az alapfelülethez és a képsíkhoz való
viszonya. Világos, hogy önmagában a c változtatása a képsík hasonlósági
transzformációját eredményezi, tehát a vetületi torzulások eloszlását
elsősorban az f nagysága befolyásolja.
Helyezkedjen
el a képsík a gömb forgástengelyére merőlegesen (vagyis essen egybe a vetítési
fősugár a forgástengellyel) – ez az ún. normális
vagy poláris helyzet. Ha a P pont
egy parallelkörön megy körbe, akkor a rajta áthaladó vetítősugarak egy
forgáskúp palástját írják le, amelynek forgástengelye egybeesik a vetítési
fősugárral, így a képsíkot egy K középpontú körben metszi. A parallelkörök képei ezért koncentrikus körök lesznek. Ha a P pont
egy meridiánon halad végig, akkor a vetítősugarak a meridián (mint gömbi főkör)
síkjában maradnak, ezért a meridián e
síknak a képsíkkal alkotott metszésvonalára, a K pontba futó egyenesre képeződik le. A körsereg az egyenes-sereget
mindenütt merőlegesen metszi, tehát a normális perspektív
síkvetület térképi fokhálózata ortogonális.
A
képsík merőleges a meridiánsíkokra, emiatt a meridiánok Dl szöge
(a meridiánsíkok által bezárt szög) megegyezik a térképi meridiánképek
(a meridiánsíkoknak a képsíkkal alkotott
metszésvonalai) által bezárt Dl’ szöggel. Ezt a tulajdonságot
nevezzük azimutálisság-nak.
A
térképi síkkoordináta-rendszer origója a K vetületi kezdőpontba kerül, az x-szel jelölt ordinátatengely
negatív fele a kezdőmeridián képével esik egybe
(ábra???). Jelöljük r-val a b pólustávolságú (j=90°–b szélességű) parallelkör KP’
térképi sugarát. A r(b) függvényt sugárfüggvénynek nevezzük. A b, l földrajzi koordinátájú pont térképi x,y
síkkoordinátáit ekkor az
![]()
vetületi egyenletek adják meg. Ezek után a perspektív
síkvetületek megadásához elegendő a r(b) sugárfüggvényt megadni.
A
térképi fokhálózat ortogonalitása miatt a fokhálózati
vonalak vetületi főirányok, amelyek
irányában fellépő hossztorzulások megadják az a maximális és a b minimális hossztorzulást. A fokhálózat menti
hossztorzulásokat az ???ábra alapján kapjuk meg. A
parallelkör menti h
hossztorzulás:
![]()
A
meridián menti k
hossztorzulás:
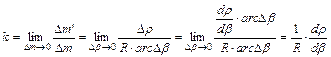
Ezek
alapján lehet az adott sugárfüggvényű perspektív
vetületek torzulásait meghatározni.
A sztereografikus síkvetület
Érintse
a képsík a gömböt az N pólusban, és kerüljön a Q vetítési középpont az ezzel
átellenes pontba, a másik pólusba. A P pont b
pólustávolsága az NP körívhez tartozó középponti szög. Ugyanehhez a
körívhez tartozik a
PQN kerületi szög, amely az ismert geometriai tétel miatt fele
akkora, mint a megfelelő középponti szög.
A képsík érintőleges volta miatt NºK; a P’KQ derékszögű
háromszögben tehát
![]() ,
,
ahonnan megkapjuk a r sugárfüggvényt:
![]()
A
fokhálózat menti hossztorzulások:
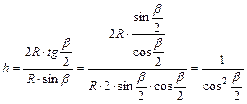
és
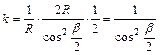 .
.
Ezek
egyenlősége miatt tehát a vetület szögtartó.
A területtorzulási modulus:
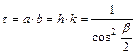
A
vetületi kezdőpontban nincs torzulás, ettől távolodva a hossz- és
területtorzulások eleinte lassan, majd gyorsulva növekednek (???ábra).
A Q vetítési középpont környéke már nem ábrázolható. Az egyenlítőn (b=90°) az l=h=k hossztorzulás kétszeres, a t területtorzulás négyszeres. A geokartográfiában emiatt félgömbnél nagyobb területet ebben
a vetületben nem szoktak ábrázolni.
A
hossztorzulás a topográfiai térképek használata szempontjából kedvezőtlen l=h=k=1.0001 értéket az
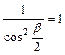
egyenlet megoldása alapján a b=1.1459° távolságon éri el, ami a pólus körüli
A
szögtartás mellett a vetület másik fontos tulajdonsága a körtartás: minden alapfelületi körív képe a térképen is körív lesz
(kivéve az egyenesre leképeződő meridiánokat). A körtartás a fokhálózat szerkesztését megkönnyíti; ennek főleg
transzverzális és ferdetengelyű elhelyezésnél van – illetve volt a számítógépes rajzoltatás elterjedése
előtt – jelentősége.
Ferdetengelyű sztereografikus vetület
Érintse
most a képsík a gömböt egy, a pólustól különböző, de nem az egyenlítőn fekvő
pontban. Ezt a pontot jelöljünk N*-gal, és tekintsük
egy segédföldrajzi koordinátarendszer segédpólusának. Legyen a Q vetítési
középpont a gömbfelület N*-gal
átellenes pontjában (???ábra). Az így keletkezett perspektív
vetületet ferdetengelyű sztereografikus
síkvetületnek nevezzük. A P pont b* segédpólustávolsága
az N*P körívhez
tartozó középponti szög; a PQ N* szög
pedig az ugyanezen körívhez tartozó kerületi szög, amelynek nagysága az imént
idézett geometriai tétel szerint b*/2. Legyen a képsíkon P’ a leképezett pont; jelölje ugyanott
KºN* az érintési pontot (a
vetületi kezdőpontot) és rºP’K a sugárfüggvényt. A P’KQ derékszögű
háromszögből
![]()
Az
N*N kezdő-segédmeridián (egyben meridián) képe egyenes, ezt választjuk az x ordináta-tengely negatív felének. Ez az irány a P’N
segédmeridián-kép irányával az azimutálisság miatt l*
szöget zár be; a vetületi egyenletek tehát:
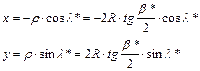
(Ez
egy DNy-i tájolású koordinátarendszer: a D-i irányba mutató tengelyt jelöljük x-szel, a Ny-it y-nal.)
Alakítsuk
át x-ben és y-ban a sugárfüggvényt:
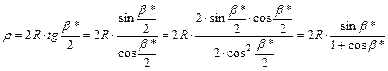
Visszahelyettesítve:
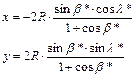
A
megfelelő gömbháromszögtani tételek segítségével az x, y
síkkoordinátákat a b, l (illetve a
j , l) földrajzi koordináták függvényeként írjuk fel. Tekintsük ehhez az N*PN polárgömbháromszöget
(???ábra). A gömbháromszögtani oldal-cosinus-tételből:
![]()
A
sinus-tételből:
![]()
Ezt
átrendezve:
![]()
Végül
a második alapformából kapjuk, hogy:
![]()
Szorozzuk
ezt végig sinb -val:
![]()
(Ismét
felhasználtuk a fenti sinus-tételt, majd egyszerűsítettünk sinb-val.) Innen kifejezhető sinb*×cosl*:
![]()
Ezeket
behelyettesítve a vetületi egyenletekbe és figyelembe véve, hogy l*
és Dl ellenkező előjelűek:
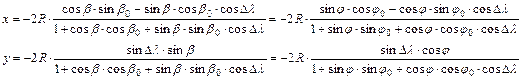
Itt b0,l0 (illetve j0,l0) jelöli a vetületi
kezdőpont szerepét játszó segédpólus földrajzi koordinátáit, Dl=l-l0 pedig a segédpóluson átmenő
középmeridiántól mért hosszúságkülönbséget.
Ha
az x,y síkkoordinátákból a b, l (illetve a j, l) földrajzi koordinátákat akarjuk kiszámítani,
akkor kiindulhatunk a sugárfüggvényre vonatkozó Pythagoras-tételből:
![]()
Innen
kifejezhető b*:
![]() ,
,
a
vetületi egyenletekből pedig l*:
![]()
A segédföldrajzi
koordinátákból a földrajzi koordinátákat a fenti polárgömbháromszögből
számolhatjuk ki oldal-cosinus- illetve sinus-tétellel:
![]()
majd
![]()
vagy
![]()
Innen
kapjuk a l
hosszúságot:
![]()
A
ferdetengelyű sztereografikus síkvetület inverz
vetületi egyenletei explicit alakban is felírhatók. Ezek meghatározásához
szintén a síkkoordináták négyzetösszegéből induljunk ki:
![]()
A 4×R2-tel való átosztás után vezessük be az alábbi
jelölést:
![]()
Ekkor
az átszorzás után az egyenlet alakja:
![]()
Innen
kifejezhető cosj ×cosDl:
![]()
Helyettesítsük
most a fenti x
vetületi egyenletbe a cosj ×cosDl kifejezését:
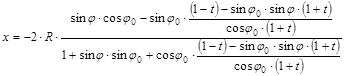
A jobb oldal nevezőjével
átszorozva és közös nevezőre hozva:
![]()
![]()
Elvégezve
a kijelölt műveleteket:
![]()
Összevonások
után kifejezzük sinj-t:
![]()
Végül
![]()
Hasonlóan
helyettesítsük az y vetületi egyenletbe a fenti cosj ×cosDl -t,
miután a számlálót cosDl -val
bővítettük:
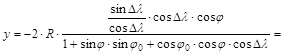
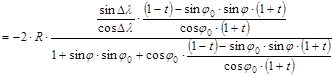
Átszorzás
és közös nevezőre hozás után:
![]()
![]()
A
kijelölt műveletek elvégzése és sinj imént kapott képletének behelyettesítése
után:
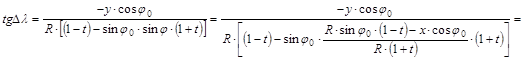
![]()
![]()
Ebből
kapjuk a Dl szöget:
![]()
A ferdetengelyű sztereografikus vetület
magyarországi alkalmazása a topokartográfiában
Lényegében
ezt a vetületet használta a magyarországi felsőrendű háromszögelés 1857-től,
majd erre tért át az országos felmérés 1863-tól. A felmérés alapfelülete a Bessel-ellipszoid volt. Erről az ún. „kettős vetítéssel”
tértek át a síkra.
Az első leképezésben a Bessel-ellipszoidi
koordinátákhoz a Gauss féle szögtartó
gömbvetülettel rendelték hozzá a gömbi koordinátákat. A képfelület itt az
ún. első magyarországi Gauss-simulógömb (R=6378512.966m) volt. A leképezés
paraméterei:
n=
1.000 751
489 594
k= 1.003 016
135 133
Használjuk
még a számolásokhoz a Bessel-ellipszoid első
excentricitását:
e= 0.081 696 683 121 57
A második lépésben történt a képsíkra
vetítés ferdetengelyű sztereografikus
vetülettel. Az akkori országterületen a
hossztorzulások csökkentése érdekében két képsíkot vettek fel. Az ún.”budapesti
rendszer” vetületi kezdőpontja (és egyben a DNy-i tájolású
síkkoordináta-rendszer origója) a gellérthegyi pont gömbi képébe (j0=47°26’21.1372”;
l0= +0°
1936-tól
vezették be az ún. katonai
sztereografikus rendszert: a budapesti rendszerben felmért területeken az
origót eltolták a gellérthegyi pontból Ny-ra és D-re 500-500 km-rel, és a
koordinátatengelyek irányának megfordításával a tájolását ÉK-ivé tették. A
gellérthegyi pont koordinátái tehát e koordinátarendszerben (