A VETÜLETTAN TÁRGYA

Az alap- és a képfelület

A geodéziának és a térképészetnek szüksége van olyan leképezésekre ("vetületekre"), amelyek segítségével a görbült földfelületen elhelyezkedő geometriai objektumokat (pontokat, vonalakat vagy felületdarabokat) síkban lehet megjeleníteni olymódon, hogy a síkbeli méretviszonyok (hosszak, irányok ill. szögek, területek nagysága) a földfelületi méretviszonyoktól kevéssé térnek el, és így azokra térképi mérések alapján vissza lehet következtetni. Ezekkel a leképezésekkel és tulajdonságaikkal foglalkozik a vetülettan, más néven matematikai kartográfia.

Vegyünk egy leképezést, amely egy felület (az ún. alapfelület) pontjait egy másik felületre (az ún. képfelületre) képezi le, vagyis az alapfelület minden pontjához a képfelület egy pontját rendeli hozzá. Tegyük fel, hogy mindkét felület lehetőleg folytonos, szabályos és zárt matematikai képlettel vagy sorral leírható. (Minthogy a geoid-felületre az utóbbi két feltétel nem teljesül, így az a vetülettannak közvetlenül nem képezi tárgyát.)

A felületek zárt képlettel többféle módon adhatók meg. Legelőnyösebb a (Gauss-féle) ún. paraméteres alak, amelyben a felület pontjainak x, y, z koordinátáit az u,v valós paraméterek folytonos függvényeként adjuk meg:

A v paraméter rögzített értékeinél a felületen a folytonos u-vonalak seregét, az u paraméter rögzített értékeinél a folytonos v-vonalak seregét kapjuk, amelyek a felületet egyrétűen fedik le (??? ábra). A felület minden pontján áthalad egy u- és egy vele nem párhuzamos v-vonal. Sem az u-vonalak, sem a v-vonalak nem metszhetik egymást.

Például a sík paraméteres alakja:

Az r sugarú, origó-centrikus gömb is megadható paraméteres alakban, ahol a paramétereket célszerű a j földrajzi szélességnek és a l földrajzi hosszúságnak választani:

A felületeket meg lehet adni

egyenlet alakjában is, ami egy skalár-vektor függvény nívófelületét jelenti, és gyakran egyszerűbb a paraméteres alaknál. A sík egyenlete pl.:

Az r sugarú, origó-centrikus gömb egyenlete:

A felületek x, y, z koordinátájú pontjainak egy további megadási módja a kétváltozós

(Euler-Monge féle) függvény-alak, amely az egyenlet-alak speciális esetének tekinthető. Hátránya, hogy egyes felületek csak többértékű függvénnyel írhatók le. A síkot ebben az esetben a

,

a gömbfelületet pedig a

függvény adja meg.

A vetülettan elsősorban földi vetületekkel foglalkozik, amelyek a geoid-felületet közelítő szabályos alapfelületet (gömböt vagy forgási ellipszoidot) síkra képezik le. (Kivételt képeznek az ún. gömbvetületek, amelyek a forgási ellipszoid felületének pontjaihoz gömbfelületi pontokat rendel hozzá.) Forgási ellipszoidhoz úgy jutunk, hogy egy ellipszist valamelyik tengelye (földi ellipszoid esetén a rövidebbik tengelye) mint forgástengely körül megforgatjuk. Képfelületként a sík mellett számításba jönnek még az ún. síkba fejthető felületek, amelyeket úgy lehet síkká alakítani, hogy eközben a felületen belüli méretviszonyok nem változnak meg (tehát a síkba fejtés során mind a felületi görbék ívhossza, mind az egymást metsző felületi görbék metszéspontbeli érintőinek szöge, mind pedig a felületdarabok felszíne változatlan marad). Ilyen síkba fejthető felület pl. a forgáshenger és a forgáskúp palástja.

A vetületek megadása

A vetületek elnevezése (más nyelveken is) azt sugallja, mintha a vetületeknek közvetlen köze volna a centrális vetítésnek nevezett geometriai transzformációhoz. Valójában a korszerű vetület-fogalom egy felület pontjainak egy másik felület pontjaira történő matematikai leképezésén alapul. A vetületek között azonban speciális helyet foglalnak el az ún. "perspektív vetületekek", amelyeket az alap- és képfelület megfelelő elhelyezése útján centrális geometriai vetítéssel elő lehet állítani. Ezek fontos szerepet játszottak a vetülettan elméletének kifejlődésében, és közülük néhány ma is használatban van. A perspektív vetületek képfelülete egyaránt lehet sík, henger-palást vagy kúppalást. A vetületek többségét képező nem-perspektív vetületek képfelületét viszont kizárólag síknak tekintjük.

A vetületeket úgy kell megadni, hogy az alapfelület pontjairól a képfelületek pontjaira történő átszámítás minden ábrázolandó pontra lehetséges és egyértelmű legyen. Ez perspektív vetületek esetén geometriailag is megvalósítható volna, de a nem-perspektív vetületekre való tekintettel más megoldást kell választani, ami a "vetületi egyenleteknek" nevezett függvények alkalmazásával válik lehetővé. Ezek a térképi síkkoordinátákat a földrajzi szélesség és hosszúság függvényében adják meg:

és

A vetületi egyenletekkel szemben az alábbi követelményeket támasztjuk:

1. Létesítsenek kölcsönösen egyértelmű megfeleltetést az ábrázolandó területre vonatkozólag az alap- és a képfelület pontjai között.

2. Lehetőleg egyetlen zárt matematikai képlettel vagy sorral leírhatók legyenek.

3. Legyenek az ábrázolandó terület minden pontjában kétszer folytonosan differenciálhatók.

Ezeknek a követelményeknek a gyakorlati térképkészítés vetületei nem tesznek mindig tökéletesen eleget.

- A kölcsönös egyértelműség pl. nem teljesül a világtérképek két határoló meridiánképére, amelyek az alapfelület egyetlen meridiánjának felelnek meg. A pólus képe gyakran egy vonal, ilyenkor egyetlen alapfelületi pontnak végtelen sok képfelületi pont felel meg.

- Vannak olyan vetületek, amelyeknek nincsenek egységes vetületi egyenletei, hanem gömbövenként vagy foktrapézonként más és más vetületi egyenlet érvényes.

- E vetületek között vannak olyanok, ahol a vetületi egyenletek megváltozása a határoló fokhálózati vonalakon nem kétszer folytonosan differenciálható módon történik, emiatt a torzulások itt ugrásszerűen változhatnak.

Bizonyos esetekben a vetületi egyenletek inverzei is felírhatók explicit alakban, ekkor a

és

függvények segítségével a térképi pontok alapfelületi ősképeinek földrajzi koordinátáit tudjuk kiszámítani.

A vetületi torzulásokról általában

A görbült földet modellező szabályos alapfelületről a síkra, vagy síkba fejthető más képfelületre történő leképezés során az alapfelületi objektumok bizonyos méretviszonyai megváltozhatnak, ezeket a változásokat vetületi torzulásoknak nevezzük. Könnyen belátható, hogy bizonyos hosszak minden vetületben torzulnak.

Egy adott felület görbeívei közül azt nevezzük geodéziai vonalnak, amely a két végpontot összekötő felületi görbeívek közül a legrövidebb. Sík esetén a geodéziai vonal a két végpontot összekötő egyenes szakasz, gömbfelület esetén pedig a két végponton áthaladó gömbi főkör ívek közül a rövidebbik - ezt nevezzük ortodrómának. (Bonyolultabb a helyzet a forgási ellipszoid felületénél, mert ott a geodéziai vonal általában nem síkgörbe.)

Tételezzük fel most, hogy létezik olyan "hossztartó" vetület, amelynél a gömbnek választott alapfelületi ívek hosszai mindig megegyeznek ezek képfelületi megfelelőinek ívhosszával. Ha volna ilyen leképezés, annál az alapfelület geodéziai vonalainak képe szükségszerűen a képfelület geodéziai vonala kellene legyen. Földi vetület esetén tehát a gömb-alapfelületi ortodróma-íveknek egyenes szakaszokra kellene leképeződniük.

Tekintsünk most a gömb alapfelületen egy olyan gömbháromszöget, amelynek egyik csúcsa a pólusban, a másik két csúcsa az Egyenlítőn helyezkedik el egymástól 90°-nyira. Ennek a (szabályos) gömbháromszögnek mindhárom oldala és szöge 90°-os. A fentiek szerint a feltételezett "hossztartó" vetületünknek ezt egy olyan szabályos síkháromszögre kellene leképeznie, amelynek oldalhossza megegyezik a gömbháromszög oldalhosszával. Vegyünk most egy olyan ortodróma-ívet, amely a pólustól a gömbháromszög szemközti oldalának egy belső pontjához vezet (??? ábra). Ennek alapfelületi hossza megegyezik a gömbháromszög oldalhosszával (90°), azonban a képfelületen egy olyan egyenes szakaszra képeződik le, amely a síkháromszögekre vonatkozó ismert tétel miatt a háromszögünk oldalánál kisebb. Ez ellentmond a kezdeti "hossztartósági" feltételünknek, következésképpen kimondhatjuk, hogy "hossztartó" vetület nincs. (Ugyanez a gondolatmenet forgási ellipszoid alapfelület esetén is érvényes.) A szükségszerűen fellépő hossztorzulások mellett a térképen az irányok ill. a szögek és a területek is torzulhatnak.

A vetületek legfontosabb tulajdonságai a torzulási viszonyaikra vonatkoznak. Egy vetület alkalmazása előtt tudnunk kell, hogy milyen alapfelületi objektumok torzulnak és milyen mértékben, hol helyezkednek el a torzulásmentes helyek. A vetület torzulási tulajdonságai és a térkép bármely pontjában fellépő torzulási viszonyok a vetületi egyenletekből levezethetők.

A térkép méretaránya

A mindennapi életben a műszaki tervekre, helyszínrajzokra, stb. használt méretarány-fogalom a rajzi távolságnak és a megfelelő valódi távolságnak a hányadosa. Ettől eltér a térképi méretarány fogalma. Ehhez gondoljuk végig a térképkészítés elvi folyamatát.

Első lépésben a görbült földfelületet vagy egy részét síkra képezzük le. Ez a leképezés egy földi méretű képzeletbeli síkra történik, amelyen aztán a gyakorlati használhatóság céljából egy arányos kicsinyítést hajtunk végre; ez eredményezi a kézben tartható vagy képernyőn szemlélhető térképet (??? ábra). A térkép tehát egy vetület és egy hasonlósági transzformáció egymás utáni alkalmazásából keletkezik. Ennek a hasonlósági transzformációnak az arányát nevezzük a térkép (névleges v. elméleti) méretarányának. Vagyis képletben:

A térkép méretaránya tehát egyetlen, az adott térképre jellemző szám (arány). Viszont a térképi hossznak a megfelelő alapfelületi valódi hosszhoz való aránya - ahogyan a köztudatban a méretarány fogalma él - a vetületi torzulások miatt attól függ, hogy a vizsgált vonal, amelynek a hosszáról itt szó van, a térkép melyik részén helyezkedik el. Ha van a térképünknek hossztartó vonala, akkor az e mentén vett ívek térképi és valódi hosszának aránya megegyezik a térkép névleges méretarányával. A torzulásmentes vonalat izodeformációs vonalnak is hívják. Izodeformációs övnek azon térképi pontok összességét nevezik, ahol a névleges méretarány a térkép és a valóság közötti hossz-átszámításhoz gyakorlati szempontból használható. Ennek kiterjedése egy adott vetület esetén természetesen függ az elvárt pontosságtól: növelésével az izodeformációs öv keskenyebbé válik.

ALAPFOGALMAK AZ ALAP- ÉS KÉPFELÜLETEN

Az alapfelület paraméterezése

Gömb alapfelület esetén a paraméterezés a gömbközéppontban felvett origójú térbeli polárkoordináta-rendszeren alapul, melynek polártengelye kijelöli az (É-i) pólust (???ábra). Vegyünk fel egy tetszőleges P pontot a gömb felületén. Az origótól a P-hez vezető rádiuszvektornak a polártengellyel bezárt b szöge (a pólustávolság), illetve ennek pótszöge, a j(=90°-b) földrajzi szélesség adja az egyik paramétert. A koordinátarendszer kezdő-félsíkja (melynek határa a polártengelyre esik) a gömbfelületen kijelöli a kezdőmeridiánt. Most az alapfelületi P pontot tartalmazó, a polártengely által határolt félsíknak a kezdő-félsíkkal bezárt szöge adja a másik paramétert, a l földrajzi hosszúságot. (A harmadik polárkoordináta, a rádiuszvektor r hossza , amely megegyezik a gömb sugarával, minden P pontra azonos, így ez a P pont megadásánál figyelmen kívül hagyható.)

A j földrajzi szélességet előjellel látjuk el, amelyet az É-i félgömbön tekintünk pozitívnak (vagyis –90°£j£90°, és 0°£b£180°). Az azonos földrajzi szélességű (vagy azonos pólustávolságú) pontok által meghatározott gömbi körök a szélességi körök vagy parallelkörök. (Ezek között kitüntetett szerepet játszik a 0°-os szélességi kör, az egyenlítő.) Az R sugarú gömbön a j szélességi kör r sugara: r=R×cosj=R×sinb, az egyenlítő sugara így R. A l földrajzi hosszúságot a K-i féltekén tekintjük pozitívnak (vagyis -180°£l£180°). Az azonos földrajzi hosszúságú pontok által meghatározott gömbi főkörívek (félkörök) a hosszúsági körök vagy meridiánok. A hosszúsági kör sugara mindig R.

A kezdőmeridiánnal nem keverendő össze a középmeridián, amely az ábrázolt terület középvonalában haladó, többnyire kerek értékű hosszúsági kör. Ez általában a fokhálózat képének szimmetriatengelye, így a képfelületen egyenesként jelenik meg.

A gömbfelületi pontokat természetesen meg lehet adni térbeli derékszögű koordinátákkal is, ekkor a koordinátarendszer origóját célszerűen szintén a gömbközéppontban vesszük fel; a z tengely a polártengellyel esik egybe, az x tengelyt pedig rendszerint a kezdőfélsík iránya jelöli ki. Az xy sík ekkor az egyenlítő síkjára esik.

Forgási ellipszoid alapfelület esetén ugyancsak térbeli polárkoordinátarendszerből indulunk ki, melynek origója az ellipszoid centrumával, polártengelye az ellipszoidfelület forgástengelyével esik egybe. A pólustávolságnak megfelelő B paramétert most a gömbfelületnél látottól eltérően az ellipszoidfelület P pontbeli normálisának a polártengellyel bezárt szöge adja meg, ennek pótszöge a F(=90°-B) (ellipszoidi) földrajzi szélesség, amelyet a gömbnél elmondott módon előjelezünk A L (ellipszoidi) földrajzi hosszúságot a gömbhöz hasonlóan, a P pontot tartalmazó félsíknak a kezdő félsíkkal alkotott (előjeles) szög segítségével definiáljuk. Az ellipszoidfelületi pontok derékszögű és polárkoordinátái közötti átszámításnak a műholdas tájékozódásban van szerepe .

Az azonos földrajzi szélességű illetve azonos pólustávolságú pontok itt is egy szélességi kör vagy parallelkör mentén helyezkednek el, melyek az ellipszoidfelület forgástengelyre merőleges körmetszeteként is előállíthatók. Jelöljük a-val illetve b-vel a forgási ellipszoid nagyobb illetve kisebb féltengelyét. A szélességi kör r sugarát és síkjának az egyenlítő síkjától mért z távolságát az alábbi képletek adják meg:

és

(Az egyenlítő sugara tehát a.) Az azonos földrajzi hosszúságú pontok most egy fél-ellipszis alakú meridiánt határoznak meg, melynek az egyenlítő síkjában fekvő nagy féltengelye a, a forgástengelyen lévő kis féltengelye b (???ábra).

Az ellipszoidi szélességet geodéziai szélességnek is hívjuk. Ez különbözik az ellipszoid középpontjától a P ponthoz vezető rádiuszvektornak az ellipszoidi egyenlítő síkjával bezárt szögétől, amelyet geocentrikus szélességnek nevezünk. (A pólusban és az egyenlítőn a geodéziai szélesség megegyezik a geocentrikus szélességgel. Természetesen gömb alapfelület esetén ez a két szélesség mindenütt azonos, mivel a P ponthoz vezető rádiuszvektor egyben merőleges a gömb felületére.) Tekintsük most azt a gömböt, amelynek középpontja a földi ellipszoid centruma, sugara pedig annak fél nagytengelye. Ekkor az ellipszoidi pontnak a forgástengellyel párhuzamos gömbfelületi vetületéhez vezető rádiuszvektor egyenlítősíkkal bezárt szöge az ún. redukált szélesség, mely a pólusban és az egyenlítőn a geodéziai szélességgel egybeesik.

Értelmezzük a geoidon elhelyezkedő P pont pólustávolságának a helyi függőleges és a sarkcsillag iránya által bezárt szöget; e szög pótszöge az ún. csillagászati (asztronómiai) szélesség (???ábra). A geoidfelület normálisa (a nehézségi erő irányát megadó függővonal) és a geoidhoz illesztett forgási ellipszoid mint elméleti referenciafelület normálisa kis mértékben különbözik egymástól, ez az ún. függővonal-elhajlás.

A geokartográfiában és a topográfiai térképműveknél általában Greenwich-i kezdőmeridiánt használnak. Régebben - főleg Európában - elterjedt volt a Ferro-i (Kanári-szigetek) kezdőmeridián használata, amely a Greenwich-itől mintegy 17°40'-re Ny-ra fekszik. K-Európa több országában Pulkovo-i kezdőmeridiánnal dolgoztak, amely Greenwich-től mintegy 30°20'-re K-re helyezkedik el. A magyarországi térképezéseknél a gellérthegyi meridián játszik fontos szerepet, amelynek a ferroi kezdőmeridiántól való eltérését a Bessel-ellipszoidon 36°42'51.69"-nek tekintették, míg a greenwichi hosszúsága az IUGG'67-es ellipszoidon 19°2'54.856"-nek van megállapítva.

Az alapfelület paraméterezése lehetséges egy alapfelületi polárkoordinátarendszer segítségével is. Vegyük fel ehhez az O origót valahol a pólustól különböző pontban, valamint egy kezdőirányt, amely rendszerint a pólus felé mutat és így egy meridiánnal esik egybe. A tetszőleges alapfelületi P ponthoz tartozó polártávolságot az OP ortodrómaív hossza adja, míg a polárszög - az ún. azimut - az OP iránynak a kezdőiránnyal bezárt szöge, az óramutató járásával megegyező irányban mérve, melyet 0° és 360° közé esőnek tekintünk (???ábra). A polárkoordinátákkal adott P pont földrajzi koordinátáinak kiszámítását első geodéziai alapfeladatnak nevezzük. Ha a földrajzi koordinátákkal adott P pont polárkoordinátáit számítjuk ki, akkor a második geodéziai alapfeladatot oldjuk meg. Gömb alapfelület esetén mind az első, mind a második geodéziai alapfeladat gömbháromszögtani összefüggésekkel oldható meg.

Gömb alapfelület esetén értelmezhető a segédföldrajzi koordinátarendszer. Ehhez először is ki kell jelölni a gömbön a segédpólust és ezzel együtt a segédpoláris tengelyt. A segédpólustól egyenlő gömbi távolságra (segédpólustávolságra) lévő pontok képezik a segédparallelköröket, 90°-os gömbi távolság esetén a segédegyenlítőt. A segédpólustávolság pótszöge a j* segédszélesség. A két segédpólust összekötő gömbi főkörívek a segédmeridiánok. Ezek közül egyet segédkezdőmeridiánnak választva, ennek félsíkja bármely segédmeridián félsíkjával a segédhosszúságnak nevezett l* szöget zárja be. A segédhosszúságot a segéd-É-i pólus felől nézve az óramutató járásával ellentétesen irányítjuk, és nagyságára: -180°£l*£180°. (Megjegyezzük, hogy az esetek túlnyomó többségében a segédkezdőmeridián tartalmazza az egyik pólust, ugyanis a pólusokon és a segédpólusokon áthaladó gömbi főkör - bimeridián - egy-egy szakasza meridián és egyben segédmeridián is.) A segédföldrajzi koordinátarendszer bevezetésének fő előnye abban áll, hogy segítségükkel bizonyos rokonvetületek egységesen tárgyalhatók, és ezek vetületi egyenletei egyszerű, egységes alakban adhatók meg.

Tetszőleges gömbfelületi (j,l) koordinátákkal megadott pont segédföldrajzi (j*,l*) koordinátáinak meghatározása a második geodéziai alapfeladatra vezethető vissza, míg a segédföldrajzi (j*,l*) koordináták ismeretében az első geodéziai alapfeladat megoldása alapján kapjuk a (j,l) földrajzi koordinátákat, mindkét esetben gömbháromszögtani összefüggések segítségével.

A képfelület paraméterezése

A képfelületet (az esetleges síkbafejtés után) paraméterezhetjük síkbeli derékszögű x,y koordinátarendszer segítségével. Az egyik koordinátatengelynek célszerűen a fokhálózat szimmetriatengelyét vagy egy azzal párhuzamos egyenest választjuk. Ennek irányát szokás hálózati északi iránynak is nevezni. A geodéziában előszeretettel tekintik a hálózati északi irányt x-nek, szemben a matematikában és a vetülettanban inkább szokásos y-nal.

A vetületek egy részénél, különösen kúppalást-képfelületnél, de általában körív alakú parallelkör-képek esetén előnyös a polárkoordinátarendszer bevezetése. A koordinátarendszer origója a körív középpontjába kerül, a polártengely többnyire a középmeridiánnal esik egybe. (Nem-koncentrikus körívek esetében az origó helyzete így a szélesség függvényében akár változhat is.)

A képfelületi síkkoordinátarendszer origóját szokás vetületi kezdőpontnak nevezni.

Nevezetes alapfelületi vonalak

A vetülettanban az alapfelületi vonalak három fajtája: az ortodróma, a gömbi (ellipszoidi) körív és a loxodróma játszik központi szerepet.

Az ortodróma - mint már említettük, a geodéziai vonal szokásos elnevezése. Gömb alapfelület esetén tehát minden 180°-nál nem nagyobb középponti szöghöz tartozó főkörív ortodróma, így a (segéd-)meridiánok és a (segéd-)egyenlítő is. A meridiánokkal és az egyenlítővel egybe nem eső gömbi főköröket szokás harántköröknek is nevezni. Forgási ellipszoid alapfelület esetén speciális ortodrómák a meridiánok (ellipszisek) és az egyenlítő (kör), az összes többi ortodróma térgörbe. Minden forgásfelületen, így gömbfelületen és forgási ellipszoidon is teljesül a Clairaut-tétel, mely szerint a geodéziai vonal bármely pontjában a vonal parallelkörökkel bezárt szögének (az a azimut pótszögének) koszinusza szorozva a pont forgástengelytől mért r távolságával állandó

Az ortodróma ívhosszát gömbön a radiánban megadott középponti szögnek az R sugárral való szorzata adja. A Dj szélességkülönséghez tartozó meridiánív s hossza így: s=R×arcDj. Forgási ellipszoidon a F₁ és F₂ szélességek közötti meridiánívhosszat az ellipszisív simulókör-sugarának (az M-mel jelölt ún meridiángörbületi sugárnak) a földrajzi szélesség szerinti integráljaként kapjuk:

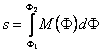, ahol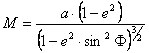

A (segéd-) parallelkörök a (segéd-) poláris tengelyre nézve forgásszimmetrikus körök, amelyek gömb alapfelület esetén (az egyelítőt kivéve) gömbi kiskörök. A j szélességű parallelkörön egy Dl hosszúságkülönbséghez tartozó ív s hossza: s=R×cosj×arcDl. Forgási ellipszoid alapfelület F szélességű parallelkörén a DL hosszúságkülönbséghez tartozó s ívhossz:

Az egyenlítő, mint speciális a sugarú parallelkör mentén ez s=a×arcDL -vá egyszerűsödik.

Loxodrómának azokat az alapfelületi vonalakat nevezzük, amelyeknek minden pontjában az a azimut állandó. A meridiánok az a=0° és a=180° azimuthoz tartozó speciális loxodrómák, a parallelkörök pedig az a=90° és a=270° azimuthoz tartozó speciális loxodrómák. A többi loxodróma olyan csavarvonal, amely az egyik pólusból a másik pólusba vezet. Írjuk fel gömb alapfelületre egy ilyen loxodróma egyenletét az egyértékűség miatt l=l(j) alakban. Ehhez változtassuk meg a j,l koordinátájú pontot Dj,Dl-val, ami egy kis foktrapézt hoz létre a gömbön, melynek oldalai arcDj és arcDl×cosj ; átellenes csúcsait kössük össze egy Ds hosszúságú loxodróma-ívvel (???ábra). A kicsiny foktrapéz oldalai és "átlója" közelítőleg síkban lévőnek tekinthetők, amelyben

; ezt átrendezve:

Ha most a loxodrómát kis darabokra bontjuk, akkor az összegzés, majd a minden határon túli finomítás után az integrálás az alábbi eredményre vezet:

;

innen

A C integrációs konstans megadható, ha a loxodróma pl. a j₀,l₀ koordinátájú ponton halad át, ugyanis ekkor az egyenlet az alábbi alakú:

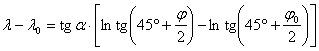
Egyenletünk szerint minden j-hez egyetlen l tartozik, és j®±90° esetén l®±¥.

A j₁,l₁ és j₂,l₂ koordinátájú pontokon áthaladó loxodróma azimutja:

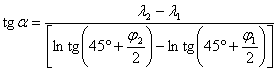
Az a azimuthoz tartozó loxodróma j₁ és j₂ szélességek közé eső darabjának ívhossza szintén az iménti ábra alapján adható meg, ugyanis:

, ahonnan

A loxodróma-ívet kis részekre felosztva, a képletet az egyes részekre alkalmazva összegzünk, ami a minden határon túli finomítás után integrálásba megy át:

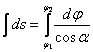
innen .

A meridiánok a pólus felé összetartanak, ennek mértékét fejezi ki a valódi alapfelületi meridiánkonvergencia. Vegyünk két pontot (P₁ és P₂) az alapfelületen és kössük össze ezeket egymással és a pólussal ortodrómaívek segítségével. A két pontbeli azimut különbségének 180° feletti része a g-val jelölt valódi alapfelületi meridiánkonvergencia. Képletben:

Gömb alapfelület esetén a P₁, a P₂ és pólus által meghatározott polárgömbháromszög szögeire (???ábra) teljesül, hogy

ahol Dl a két pont hosszúságkülönbsége és e a gömbi szögfölösleg. Átrendezve az egyenletet:

vagyis .

A vetületi meridiánkonvergencia az a m -vel jelölt szög (???ábra), amelyet a képfelületi P' ponton áthaladó meridiánkép érintője a képfelületi derékszögű koordinátarendszer hálózati északi irányt kijelölő tengelyével bezár, és amelyet az óramutató járásával ellentétesen irányítunk. A vetületi meridiánkonvergenciának a vetületek geodéziai alkalmazásánál van szerepe.