A VETÜLETI TORZULÁSOK

A bevezetőben láttuk, hogy a térképen a hosszak torzulásával mindenképpen számolnunk kell. A térképhasználat során a hosszak mérésén kívül szükség lehet a szögek és a területek mérésére is. A térképi mérésekből csak a torzulások mértéke és eloszlása ismeretében tudunk megbízhatóan következtetni az alapfelületi mértékekre, ezért a torzulások meghatározása a vetülettanban központi szerepet játszik. Ehhez először pontosan definiálnunk kell a vetületi torzulások fogalmát.

A torzulási arányok

Torzulási arány alatt a véges nagyságú objektumok térképi és alapfelületi méretének arányát értjük. A hossztorzulási arány definiálásához vegyük egy mérhető hosszúságú alapfelületi vonal ívhosszát (s) és pontonként vetített képfelületi megfelelőjének s' ívhosszát. (A vetületi egyenletek tulajdonságaiból adódóan s' általában létezik.) Ekkor az l hossztorzulási arány:

A szögtorzulási arányhoz tekintsünk két, egymást metsző sima (törésmentes) görbét, és ezeknek képfelületi megfelelőit, amelyek a vetületi egyenletek tulajdonságaiból következőleg szintén egymást metszők és simák lesznek. Az egymást metsző vonalak által bezárt szög alatt a metszéspontbeli érintőik által bezárt szöget értjük. Legyen az érintők szöge az alapfelületen d, a képfelületen d'. Ekkor az i szögtorzulási arány:

Első irányredukciónak nevezzük az érintők alapfelületi és képfelületi szögének D=d-d' különbségét.

A második irányredukció fogalmához szükség van a vizsgált O pontban egy kezdőirány megadására mind az alap-, mind pedig a képfelületen; ez rendszerint a pólus iránya, amelyet a meridián illetve a meridiánkép érintője ad meg. Vegyünk fel most a vizsgált ponton kívül egy tetszőleges P pontot az alapfelületen, melynek képe P’ (???ábra). Az O-t és P-t összekötő geodéziai vonal O’P’ képének az O’-beli érintője általában nem esik egybe az O’P’ egyenessel; az általuk bezárt szöget második irányredukciónak nevezzük. Ennek nagysága a vizsgált O pontban az O’-beli érintőn kívül függ a P helyétől is.

A területtorzulási arányt az alapfelületi idom F felszínének és a képe F’ területének alapján számíthatjuk az alábbi képlettel:

A torzulási modulusok

A torzulási modulusok a torzulásokat a térkép egyes pontjaiban jellemzik, melyeket ezért határértékként definiálunk. Ezt szokás úgy is kifejezni, hogy nem véges nagyságú, hanem „végtelen kicsiny” mennyiségekre vonatkoznak.

Tekintsünk az alapfelület P pontján áthaladó sima görbét és azon egy másik Q pontot, valamint ennek a P’-n és Q’-n áthaladó képét. Ha a Q pont a görbe mentén minden határon túl megközelíti P-t, akkor az Ds-sel jelölt PQ ívből és a Ds’-vel jelölt P’Q’ ívből a

képlet adja az l hossztorzulási modulust vagy lineármodulust.

A vetületi egyenletek tulajdonságaiból következőleg a P pontban fellépő hossztorzulási modulus nem függ attól, hogy a Q pont a P-t milyen görbe mentén közelíti meg, hanem csak a görbe P-beli érintőjének irányától. Ezt úgy is fogalmazhatjuk, hogy a hossztorzulási modulus általában a hely és az irány függvénye. Ha a hossztorzulási modulus a térkép egy pontjából kiinduló minden irányban egységnyi, vagy egy vonal mentén egységnyi, akkor hossztartó pontról vagy vonalról beszélünk.

A szögtorzulási modulus definíciója megegyezik a szögtorzulási arányéval, vagyis az egymást metsző görbék érintője által bezárt alapfelületi d és képfelületi d' szögekre vonatkozólag:

(A határátmenetet itt az érintők mint a szelők határhelyzetei képviselik.) Ha a térkép egy pontjában bármely irányok különbségére i=1 –nek adódik, akkor a térkép e pontban szögtartó. Ha a térkép minden pontjában szögtartás áll fent, akkor szögtartó vetületről beszélünk.

Vegyünk most egy P pontot tartalmazó, Df felszínű felületdarabot az alapfelületen, melynek képe egy Df’ területű idom lesz a képfelületen. Zsugorítsuk rá a P pontra az alapfelületi idomot úgy, hogy minden pontja egyenletesen konvergáljon P-hez, miközben Df®0. Ha a

határérték létezik, akkor ezt nevezzük a területtorzulási vagy területi modulusnak. Ha a térkép egy pontjában t=1, akkor a térkép e pontban területtartó. Ha a térkép minden pontjában területtartás áll fent, akkor a vetületet területtartónak nevezzük.

A vetületek tehát a torzulásaik alapján lehetnek, szögtartók, lehetnek területtartók, de –

amint azt a későbbiekben látni fogjuk – nem lehetnek egyidejűleg szögtartók és területtartók is. E két nagy torzulási csoporton kívül vannak még olyan vetületek, amelyeknél mind a szögek, mind a területek torzulhatnak; ezeket általános torzulásúaknak nevezzük.

Torzulásmentességről akkor beszélünk, ha a térkép valamely pontjában vagy valamely vonala mentén semmilyen torzulás sem lép fel, vagyis mind a hossztartás, mind a szög- és területtartás fennáll.

A vetületi torzulások kiszámítása a térkép egy pontjában

A következőkben egy adott vetületű térkép vetületi torzulásait kívánjuk kiszámítani valamely j,l koordinátákkal adott pontban. Tudjuk, hogy a hossz-, szög- és területtorzulásokat a torzulási ellipszis adatai szabják meg (???). Célunk tehát, hogy a vetületi egyenletek segítségével meghatározzuk az adott pontbeli torzulási ellipszis adatait. Ehhez szükségünk van közbeiktatott mennyiségekre, nevezetesen a fokhálózat menti torzulásokra.

Fokhálózat menti torzulások

A térkép egy pontjában a fokhálózat legfontosabb torzulási jellemzőit a fokhálózat menti torzulásokkal adjuk meg. Ezek:

- h parallelkör menti hossztorzulás

, ahol Dp a vizsgált pontot tartalmazó parallelkör menti ívdarab hossza, Dl a hozzá tartozó hosszúságmegváltozás, Dp’ pedig a megfelelő térképi ívdarab hossza;

- k meridián menti hossztorzulás

, ahol Dm a vizsgált pontot tartalmazó meridián menti ívdarab hossza, Dj a hozzá tartozó hosszúságmegváltozás, Dm’ pedig a megfelelő térképi ívdarab hossza;

- a fokhálózati vonalak képe által a térképen bezárt Q szög

(Megjegyezzük, hogy torzulási szempontból valójában nem a Q szög értéke, hanem ennek 90°-tól való eltérése lényeges. Ezt jobban kifejezi a ctgQ értéke, amelynek értéke annál jobban eltér 0-tól, minél jobban eltér Q a derékszögtől. Ugyancsak használatos a sinQ szögfüggvény is.)

E mennyiségek – mint majd az alábbiakban látjuk – közvetlenül kiszámíthatók a vetületi egyenletek segítségével, másrészről belőlük közvetlenül kiszámíthatók a torzulási ellipszis adatai.

A vetületi egyenletek és a fokhálózat menti torzulások összefüggései

Tekintsünk az alapfelületen egy P(j,l) pontot, és változtassuk meg ennek szélességét Dj-vel, hosszúságát pedig Dl-val, így kapjuk a P₁(j+Dj,l+Dl) pontot. Az eredeti és a megváltoztatott szélességek és hosszúságok egy kis foktrapézt határolnak (???ábra). Képezzük le ezt a foktrapézt a képfelületre; a vetületi egyenletek tulajdonságai miatt a foktrapéz oldalai közelítőleg egyenes szakaszokra képeződnek le, így eredményként közelítőleg négyszöget kapunk. Írjuk fel a Dj szélességmegváltozás és a Dl hosszúságmegváltozás eredményeként bekövetkezett Dx és Dy térképi koordinátaváltozásokat:

(Felhasználtuk a vetületi egyenletek folytonos differenciálhatóságát.) Hasonlóan kapjuk:

Az (???) ábráról látható tehát, hogy mind Dx, mind Dy egy (előjellel rendelkező) parallelkör irányú és egy meridián irányú megváltozásból adódik össze, amelyek a négyszög egy-egy oldalának a koordinátatengelyeken jelentkező merőleges vetületei. A szemközti oldalak merőleges vetületei mindkét tengelyen egyenlőnek tekinthetők, következésképpen egyenlő hosszúságúak, emiatt a foktrapéz képe közelítőleg parallelogramma.

Pythagoras tételét alkalmazva a parallelogramma oldalainak meghatározására kapjuk, hogy

Innen felírható a h parallelkör menti és a k meridián menti hossztorzulás:

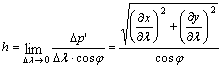
A fokhálózati vonalak által bezárt Q szöget írjuk fel azon és irányszögek különbségeként, amelyek a parallelogramma két oldala és az x tengellyel párhuzamos egyenes között keletkeznek (???ábra). Ekkor

Az ábra alapján a parallelogramma oldalairól és ezek x és y tengely irányú összetevőiről leolvashatók az alábbi összefüggések:

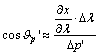
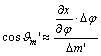
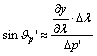
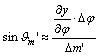
Ezeket behelyettesítve kapjuk ctgQ-ra Dj®0, Dl®0 esetén:

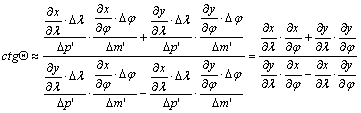
A ctgQ -ból közvetlenül kiszámítható a sinQ az alábbi képlettel:

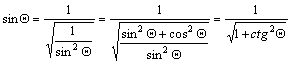
A fenti mennyiségekkel – az alapfelületi kis foktrapéz DF felszíne és a képfelületi kis parallelogramma DT területe segítségével – felírható a t területtorzulási modulus.

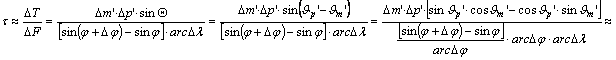
(Itt felhasználtuk, hogy

.)

Egyszerűsítés után kapjuk a t területtorzulási modulusra, hogy Dj®0, Dl®0 esetén

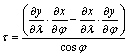
A fokhálózat menti tozulások és a torzulási ellipszis adatai közötti összefüggések

Vegyünk fel egy egységsugarúnak tekintett alapfelületi kicsiny kört a közelítő x,h síkkoordináta-rendszerben, melynek origója a kör középpontjába esik. Ennek képe egy ellipszis lesz a térképi x’,y’ koordinátarendszerben, melynek origója az ellipszis középpontja, tengelyei pedig egybeesnek az ellipszis tengelyeivel (???ábra). Az ellipszis azon rádiuszvektorai, melyek az origón átmenő fokhálózati vonalak képeire esnek, közelítőleg megegyeznek a h parallelkör menti és a k meridián menti hossztorzulással. Vezessük be az alapfelületi közelítő síkkoordinátákra a x_p’,h_p’, ill. x_m’,h_m’ síkkoordinátákra az x_p’, y_p’, ill. x_m’, y_m’ jelölést, és írjuk fel a rádiuszvektorokra a Pythagoras tételt, figyelembe véve a

egyenlőségeket (ahol a és b a torzulási ellipszis kis és nagy féltengelye):

(Az utolsó egyenlőségnél felhasználtuk, hogy és merőleges szárú szögek.)

Adjuk össze a két egyenlőséget, és kapunk egyrészt h és k, másrészt a és b között egy összefüggést:

A fokhálózati vonalak képe által bezárt szög szinusza (???ábra):

Átszorozva h×k -val:

(Felhasználtuk, hogy és , mert és merőleges szárú szögek.)

Ezzel kaptunk egyrészt h és k, másrészt a, b és Q között egy másik összefüggést.

Az összefüggésekből meghatározható a és b. Az első egyenlethez hozzáadva ill. levonva a második egyenlet kétszeresét, kapjuk, hogy:

ill.

Vonjunk gyököt mindkét egyenletből:

Ezeket összeadva ill. kivonva, végül 2-vel osztva kapjuk, hogy:

Három független mennyiségből, a fokhálózat menti torzulásokból így kaptuk a torzulási ellipszis méretét megadó a és b féltengelyt. A torzulási ellipszis harmadik jellemzőjéhez, a fokhálózathoz viszonyított állásához az alábbi módon jutunk.

Tekintsük a torzulási ellipszis tetszőleges l rádiuszvektorát, amely egyben a megfelelő alapfelületi irányhoz tartozó hossztorzulási modulus. Jelölje d’ a rádiuszvektornak az első vetületi főiránnyal bezárt szögét, d pedig ennek alapfelületi ősképét. Pythagoras tételéből

.

(Ismét felhasználtuk a és egyenlőségeket.) Tehát az első vetületi főiránnyal az alapfelületen d szöget bezáró irányban a hossztorzulási modulust a

képlet adja meg.

Jelölje most u’ az első vetületi főiránynak a meridiánkép irányával, v’ pedig a parallelkörkép irányával bezárt szögét, és jelölje u és v a megfelelő alapfelületi szögeket (???ábra). Az l-re vonatkozó képletet alkalmazzuk parallelkör menti h és a meridián menti k hossztorzulásra:

Hasonlóan (figyelembe véve, hogy u+v=90°)

Mindkét képletből kifejezhető sin²u:

Azonos gondolatmenet alapján kapjuk cos²u-t:

Most mindkettőből kifejezhetjük cos²u-t:

Ezeket egymással elosztva és gyököt vonva kapjuk a legalkalmasabb képleteket tg u-ra:

Analóg módon kapjuk a tg v-re vonatkozó képleteket:

Az alapfelületen u (vagy v=90°-u) ismeretében ki tudjuk jelölni az első vetületi főirányt.

Alkalmazzuk u-ra és v-re Tissot harmadik tételét, mely szerint az első vetületi főiránnyal az alapfelületen d, a képfelületen d’ szöget bezáró irányra teljesül a

egyenlőség:

és .

A térképen u’ (vagy v’=Q–u’) ismeretében a fokhálózati vonalak irányához felmért szögek alapján ki tudjuk jelölni az első vetületi főirányt.