A képzetes henger-, kúp- és síkvetületeken kívül még igen sok képzetes vetületet ismerünk. Közös tulajdonságuk, hogy sem a fokhálózatra, sem a vetületi egyenletekre nézve semmilyen kikötés sincsen. Ebbõl adódóan lehetnek közöttük mind szögtartók, mind területtartók, mind általános torzulásúak. A torzulási függvények: a fokhálózat menti torzulások, a maximális és minimális hossztorzulások, stb. emiatt csak a bármely vetületre vonatkozó legáltalánosabb képletek alapján számíthatók.

Célunk, hogy az egész Földet egy olyan ellipszis kontúrban jelenítsük meg, amelynek nagytengelye - az egyenlítõ képe - kétszer akkora, mint a kistengely - a középmeridián képe, és az egyenlítõ meg a középmeridián hossztartó. Arra törekszünk továbbá, hogy a kontinensek kevésbé torzuljanak, mint a korábban tanult, ugyanezen tulajdonságokkal rendelkezõ Apianus II. képzetes hengervetülete.

Kiindulásul írjuk fel a féltekét körkontúrban ábrázoló transzverzális Postel féle síkvetületet. Ehhez elõször adjuk meg sinl * és cosl * képletét transzverzális elhelyezés esetén. Az N csúccsal szemközti oldalra felírt gömbháromszögtani oldal-koszinusz tétel szerint (ld. ??? ábra):

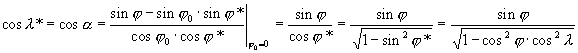
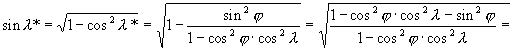
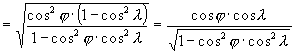
E képletek felhasználásával Postel transzverzális vetületének egyenletei:

és hasonlóan

A határoló meridiánok - a jobb és baloldali kontúrvonalak - l =± 90° behelyettesítésekor adódnak.

Hajtsunk most végre egy -szörös merõleges affinitási transzformációt az y tengelyre merõlegesen és egy -szöröset az x tengelyre merõlegesen, ami az x vetületi egyenlet -vel, az y vetületi egyenlet -vel való beszorzásával valósítható meg. Ennek hatására a félteke a kívánt alakú ellipszisre képezõdik le. Ha ezen az ellipszisen az egész Földet akarjuk ábrázolni, akkor egy Wagner-transzformációt kell végrehajtanunk m=1 és n=1/2 mellett. Képletben:

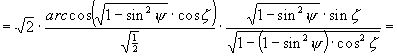
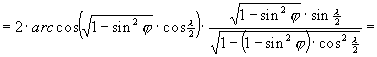
és

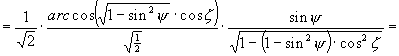
A vetületi egyenletekbõl látható, hogy és , ezért az egyenlítõ és a középmeridián hossztartó.

A torzulásokat az alábbi parciális deriváltakból számíthatjuk:

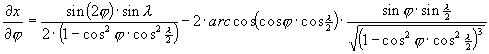
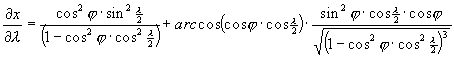
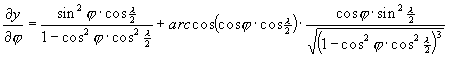
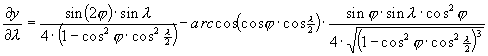
Minthogy Postel vetülete általános torzulású volt, az erre végrehajtott merõleges affinitási transzformációk és a Wagner-transzformáció ezen nem változtatott, így Aitoff vetülete is általános torzulású.

A Föld képe Aitoff vetületében a ??? ábrán látható.

Ez az 1889-ben publikált vetület David Aitoff (! 4 H @ & ) orosz kartográfustól származik. Újabban világtérképek vetületeként alkalmazzák. Átszámozott fokhálózatú változatai (ívelt pólusvonallal) kedvezõ átlagos torzultságuk miatt elterjedõben vannak.

Az Aitoff vetület mintájára hozzunk létre területtartó képzetes vetületet ellipszis-kontúrban. Ehhez induljunk ki a féltekét kör alakban ábrázoló transzverzális Lambert féle síkvetületbõl, melynek vetületi egyenletei az alábbiak:

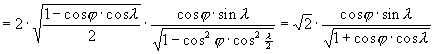
és

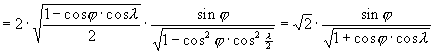
(Itt sinl * és cosl * fenti képletén kívül felhasználtuk, hogy

.)

Ismételjük meg Aitoff eljárását a transzverzális Lambert féle síkvetületre: hajtsunk végre egy -szörös merõleges affinitási transzformációt az y tengelyre merõlegesen és egy -szöröset az x tengelyre merõlegesen, valamint egy Wagner-transzformációt m=1 és n=1/2 értékekkel. Az eredmények - Hammer vetületének egyenletei - képletben:

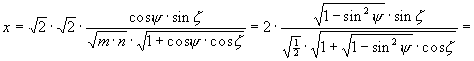
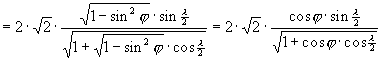
és

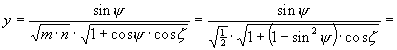
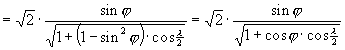
Hammer vetülete az egész Földet ellipszis kontúrban ábrázolja, éspedig – mivel mind a fenti x és y irányú merõleges affinitások együttes hatása, mind a Wagner transzformáció a területtartást megõrzi – a kapott vetület területtartó.

A torzulások részletesebb meghatározásához szükségünk lehet a parciális deriváltakra:

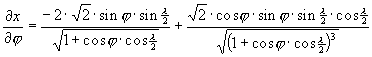
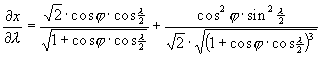
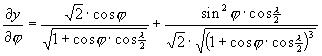
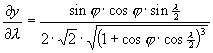
A Föld képe Hammer vetületében a ???. ábrán látható.

??? Hammer német térképész ezt a vetületet 1892-ben publikálta. Területtartó világtérképek vetületeként napjainkban igen kedvelt. Átszámozott változatban (ívelt pólusvonallal) is használják.

Pécsi Albert földrajztudós 1930-ban a Föld legfontosabb termõterületeinek ábrázolására olyan ferdetengelyû Hammer féle vetületet használt, amelynél a vetületi kezdõpont a Greenwich-i meridián 30°-os szélességén helyezkedik el. A segédegyenlítõ (és ezzel az elõnyös torzulású zóna) beállítása következtében a kedvezõ adottságú mezõgazdasági területek összességükben kevéssé torzulnak. Pécsi ezt a vetületet a “termelés térképvetületének” nevezte.

A Bartholomew cég atlaszában használt ferdetengelyû Hammer féle vetület vetületi kezdõpontja a 45° É-i szélességre, Ny-Európába kerül (“Nordic” vetület). A kontinensek alakjának deformációja itt jóval enyhébb, mint a normális elhelyezés esetén. A Föld képe e vetületben a ??? ábrán látható.

Készítsük el egy meridiánban és a j ₀ szélességi körön hossztartó valódi hengervetületnek és Aitoff vetületének a keverékét, külön átlagolva az x és az y vetületi egyenleteket. Ekkor

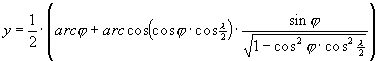
A vetület pólusvonalas; a pólusvonal egyenes, hossza a valódi hengervetület hossztartó parallelköre hosszának a fele. Az egyenlítõ ekvidisztáns, hossza a hossztartó egyenlítõ és a hossztartó parallelkör hosszának átlaga, tehát itt hosszrövidülés lép fel. A középmeridián hossztartó. A j ₀ szélességet Winkel 50° 28’-ben adta meg. Késõbb a j ₀=40° választás terjedt el.

A torzulások kiszámítása az alábbi parciális deriváltakon át lehetséges.

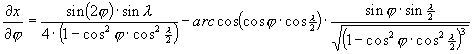
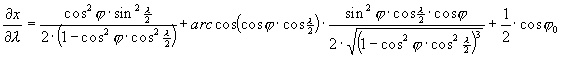
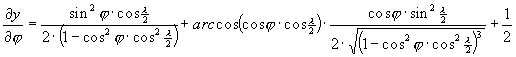
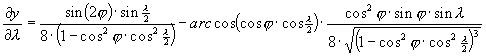
Winkel vetülete általános torzulású. Az átlagos torzultsága a gyakorlatban használt vetületek között a legkisebb, a kontinensek alakjai csak csekély mértékben deformálódnak.

A Föld képe Winkel vetületében (a j ₀=40°) a ??? ábrán látható.

Oswald Winkel "Tripel"-nek nevezett vetületét 1921-ben hozta nyilvánosságra. Az európai geokartográfia, de kivált a német nyelvterület egyik legkedveltebb vetülete világtérképek számára. Iskolai térképekhez is használják.

A parallelkörök képei ellipszisek, a meridiánok képei hiperbolák. (Az ilyen fokhálózattal rendelkezõ vetületek összességét "von der Mühl vetületcsaládnak" nevezik.) A parallelköröket ábrázoló ellipszisek és a meridiánokat ábrázoló hiperbolák közös fókuszú görbeseregek, ennél fogva a fokhálózat ortogonális.

A vetületi egyenletek:

A félteke képe a teljes sík; a fél egyenlítõ a két fókuszpontot összekötõ egyenes szakaszra, a ± 90°-os határoló meridiánok az ennek folytatásában elhelyezkedõ két félegyenesre képezõdnek le. A torzulások a parciális deriváltakból következnek:

Ezekbõl kiszámítható, hogy ctgq =0 (azaz q =90°), továbbá h=k; következésképpen a vetület szögtartó. A meridiánok a pólusok felé haladva széttartanak, emiatt a területtorzulások a magasabb szélességeken rohamosan nõnek.

A K-i félteke nagy részének képe Littrow vetületében a ??? ábrán látható.

Joseph Johann Littrow osztrák csillagász 1833-ban mutatta be vetületét. Gyakorlati jelentõsége csekély, a XX. században a vetületek csoportosításának elméleti kérdései irányították rá a figyelmet.