ELLIPSZOID-ALAPFELÜLETŰ VETÜLETEK A GEOKARTOGRÁFIÁBAN ÉS A TOPOKARTOGRÁFIÁBAN 2.

Nemzeti és nemzetközi térképművek ellipszoid-alapfelületű vetületei

Térképmű alatt térképszelvények olyan sorozatát értjük, amelyek egységes alapelveken épülnek fel, és egységes formában kerülnek kialakításra. Ide tartoznak azok a sorozatok, amelyek egy nagyobb kiterjedésű területet a megszabott méretarány miatt több szelvényre felosztva ábrázolnak. Másrészt ide sorolható egy adott területet többféle tematikával bemutató térképek együttese. Nemzetközinek akkor tekinthetjük a térképművet, ha több ország területét ábrázolja, és/vagy több ország együttműködésében készül. A térképművek egyik fontos jellemzője a térképvetület. Az M= 1 milliósnál nagyobb méretarányú térképművekhez gyakran alkalmazzák az előzőekben bemutatott ellipszoid-alapfelületű valódi vetületeket, de ezeken kívül számos más vetületet is használnak.

Az „Atlas der Donauländer” területtartó kúpvetülete

A Duna menti országok természet- és társadalomföldrajzi viszonyait M = 1 milliós méretarányban 48 különböző tematikával ábrázoló, bécsi kiadású „Atlas der Donauländer” 1970 és 1989 között folyamatosan, térképlaponként jelent meg. A 48 térképlap egységes vetületben készült, amely a korábbiakban leírt ellipszoid alapfelületű póluspontos területtartó kúpvetület némileg egyszerűsített közelítése.

Alapfelülete a nemzetközi Hayford-elliszoid. Az ábrázolt terület nagyjából a 39° és az 51° É-i szélesség között terül el. Ennek megfelelően a F_n=B_n=45°-os szélességet választották normálparallelkörnek. Az n sugárfüggvényt és a r sugárfüggvényt az alábbiak adják meg:

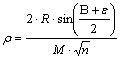
ahol R=6374.2 km az ábrázolt területre érvényes középgömb sugara, és az e korrekciós tag képlete:

A 45°-os szélességi kör itt is torzulásmentes.

A poliéder vetület

Poliédernek nevezzük a minden oldalról síkkal határolt testeket. Ezek között kitüntetett szerepet játszanak a szabályos poliéderek (amelyeknek minden lapjuk egybevágó szabályos sokszög, továbbá minden testszögletük egybevágó és szabályos) és a félig szabályos poliéderek (olyan konvex poliéderek, amelyeknek vagy lapjai szabályosak és testszögletei egybevágóak, vagy pedig lapjai egybevágók és testszögleteik szabályosak).

Bontsuk fel az alapfelületet gömbi főkörívekkel megfelelő módon szabályos részekre (gömbháromszögekre, gömbnégyszögekre, gömbötszögekre és/vagy gömbhatszögekre), és minden részt külön-külön képezzünk le egy megfelelő szabályos síkbeli sokszögre. Ha ezekből a szabályos sokszögekből egy szabályos vagy félig szabályos poliéder építhető fel, akkor szokás a leképezést „poliéder-rendszerű” vetületnek hívni. A térképezett területet ábrázoló idomok itt mind önálló vetületi síkban jelennek meg, és mindegyiknek önálló síkkoordináta-rendszere van. Ekkor egy-egy rész előnyös torzulásokkal ábrázolódik, de a síktérképek összeillesztésénél hézagok léphetnek fel.

Tágabb értelemben ide sorolhatók az ún. poliéder vetületek is, amelyeknél az alapfelületet a fokhálózati vonalak mentén – valamilyen rendszer szerint – foktrapézokra bontjuk fel, és ezeket síktrapézokra képezzük le úgy, hogy a szélességi körök képei párhuzamos egyenesek legyenek, a hosszúsági körök képei pedig összetartó egyenesek. (E tulajdonságok alapján a poliéder vetület képzetes hengervetületnek tekinthető.) A síktrapézokból – ha a szomszédos foktrapézok közös oldalai megegyező hosszúságú egyenesekre képeződnek le – itt is felépíthető egy poliéder (???ábra).

Legyen egy poliéder vetületnél a két határoló szélességi kör (F₁ és F₂) hossztartó, és legyen a határoló meridiánok (L₁ és L₂) középértéke, a L₀ középmeridián szintén hossztartó. Válasszuk a középmeridiánt y tengelynek, a déli határoló szélességi kört x tengelynek (???ábra). Az y koordináta csak a F szélességtől függ; a középmeridián hossztartása miatt

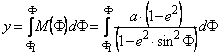
Az x koordináta kiszámításához jelöljük v₁-gyel és v₂-vel a trapéz alapjai hosszának felét, és v-vel a F szélességi kör képének a trapéz belsejébe eső fél hosszát. A hasonló derékszögű háromszögek befogóinak arányából:

ahol y₁ a F₁ és F szélesség közötti, y₂ pedig a F és F₂ szélesség közötti meridiánív alapfelületi (és a hossztartás miatt egyben képfelületi) hossza, vagyis

és ;

továbbá a határoló parallelkörök hossztartása miatt:

és

Innen v kifejezhető:

Az x koordináta úgy aránylik v-hez, mint a arc(L-L₀) az arc(DL)/2-höz, ahonnan x kifejezhető:

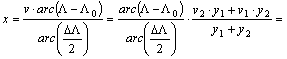
A vetület általános torzulású, a középmeridián és a határoló parallelkörök környékén a területtorzulások csekélyek.

A poliéder vetület fokhálózata egyenesekből áll, ezért könnyű a megrajzolása, ezenkívül a határoló parallelkörök és a középmeridián hossztartása miatt könnyű a földrajzi koordinátákat leolvasni, illetve a földrajzi koordinátákkal adott pontokat felszerkeszteni. Ebben a vetületben készültek az Osztrák-Magyar Monarchia harmadik katonai felmérésének 1 : 200 000, 1 : 75 000 és 1 : 25 000 méretarányú térképei, továbbá Németországban és Oroszországban, majd a Szovjetunóban (1928-ig) különböző méretarányú katonai topográfiai térképek. Földrajzi térképek később is készültek e vetületben, elsősorban a Szovjetunióban.

Ez a leképezés Lichtenstern porosz katonatiszt nevéhez fűződik, Müffling-vetületnek is nevezik.

Polikónikus vetületek ellipszoid alapfelülettel

A képzetes kúpvetületek a parallelköröket a térképen körív alakban jelenítik meg. A körívek középpontja az y tengelyen van. Rögzítsük az x tengelyt úgy, hogy vagy az ábrázolandó terület középvonalában, vagy annak D-i pereménél helyezkedjen el. Jegyezzük meg, hogy a gömb alapfelületű vetületektől eltérően a parallelköröket itt többnyire a F szélességgel jellemezzük. Jelöljük ekkor r(F)-vel a körív sugarát (a sugárfüggvényt), g-val a körív (F,L) koordinátájú pontjához vezető rádiuszvektorának az y tengellyel bezárt szögét, és c-vel a körív középpontjának az origótól mért távolságát. (A valódi kúpvetületeknél természetesen: g=n×L.) Ekkor a vetületi egyenletek:

Az ellipszoid alapfelületű képzetes kúpvetületek között kiemelt szerepet játszanak a polikónikus vetületek. A polikónikus vetületben minden parallelkör sugárfüggvénye megegyezik egy olyan kúpvetület normálparallelkörének sugárfüggvényével, amely éppen az adott szélességen torzulásmentes. Emlékeztetünk arra, hogy mind az ekvidisztáns, mind pedig a szögtartó valódi kúpvetület egy parallelkörben hossztartó változatánál a hossztartó (és egyben torzulásmentes) parallelkör sugárfüggvénye:

ahol a szokásos módon N(F_n)-vel jelöljük a F_n szélességhez tartozó harántgörbületi sugarat:

Ezt felhasználva, az ellipszoid alapfelületű polikónikus vetületek r(F) sugárfüggvénye:

A c függvényt válasszuk úgy, hogy a középmeridián legyen ekvidisztáns, és jelöljük S_m -mel a középmeridián menti hossztorzulást megadó konstanst. Vezessünk még be az általánosság kedvéért a parallelköröknél is egy S_p –vel jelölt konstans szorzót, amellyel a parallelkör menti hossztorzulást tudjuk szabályozni. Ekkor a polikónikus vetületek vetületi egyenleteinek általános alakja:

.

A polikónikus vetületek különböző változatainak további tulajdonságai a g szögtől függnek.

Szükségünk lesz még a fokhálózat menti torzulásokra. A DL hosszúságkülönbséghez tartozó parallelkör menti dp ívhossz a F szélességű parallelkörön:

Az ennek megfelelő képfelületi dp’ ívhossz a képfelületen:

A parallelkör menti h hossztorzulás tehát:

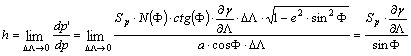
A DF szélességkülönbséghez tartozó meridián menti dm ívhossz:

Az ennek megfelelő képfelületi dm’ ívhossz:

A meridián menti k hossztorzulás tehát:

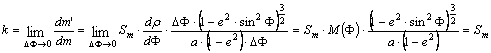
Egyszerű („simple”) vagy közönséges („ordinary”) polikónikus vetület

Az alaptulajdonság itt a parallelkörökben való hossztartás:

vagyis

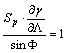
Behelyettesítve és átrendezve:

Ennek megoldása, figyelembe véve még a

követelményt:

A vetületi egyenletek tehát S_p=1 választás mellett:

.

Az egyszerű polikónikus vetület (amelyet Európában „amerikai” polikónikus vetületnek is neveznek) általános torzulású. Megalkotása Hassler svájci származású amerikai térképész nevéhez fűződik (1820). A U.S. Coast and Geodetic Survey (USGS) felmérési hivatal használta polgári és katonai topográfiai térképek vetületeként (az I. világháborútól kezdve a Lambert-Gauss féle szögtartó kúpvetület mellett) az UTM vetület 1947-es bevezetéséig.

Ortogonális polikónikus vetület

A fokhálózat ortogonalitása megfogalmazható úgy, hogy a F szélességi kör (körívre leképeződő) képének L hosszúságú pontjához vezető rádiuszvektor a függőleges tengellyel ugyanakkora g szöget zár be, mint a L hosszúsági kör érintője a F szélességű pontban (???ábra). Képletben:

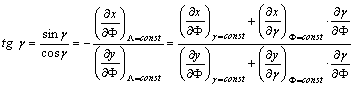
ahol felhasználtuk, hogy az x és y vetületi egyenletek egyrészt közvetlenül, másrészt a g-n keresztül közvetve függnek F-től, és alkalmaztuk a többváltozós függvények deriválására vonatkozó láncszabályt. Elvégezve a deriválást kapjuk, hogy

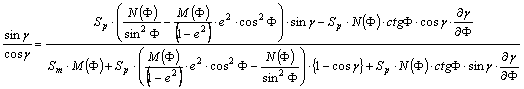
Átszorzás és átrendezés után:

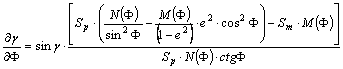
A szétválasztható változójú differenciálegyenletet integrálva:

Innen kapható a megoldás:

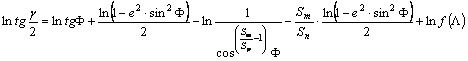
ahol f(L) tetszőleges szigorúan monoton függvény, és

Mindkét oldalt e-alapra emelve kapjuk az egyenletet, amely a g=g (F,L) függvényt megadja:

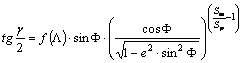
A vetületi egyenletek:

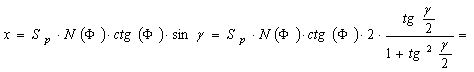
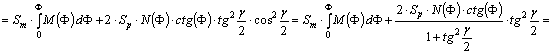
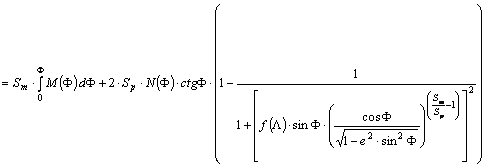
A vetület általános torzulású. Az f(L) függvényt úgy szeretnénk előírni, hogy a vetületnek legyen egy konstans hossztorzulású F_n parallelköre.

A vetületi egyenletekbe F helyére 0-t helyettesítve kapjuk, hogy

és .

Az egyenlítő mentén a h(F=0°) hossztorzulás akkor konstans, ha

Ekkor az

választás mellett kapjuk az ún. „War Office” vetületet, amelyet a brit katonai térképészet használt topográfiai térképek vetületeként az 1860-as évektől.

Legyen most F_n (¹0°) egy kiválasztott normálparallelkör, amely mentén a hossztorzulást h(F=F_n) -nek írjuk elő. Ekkor a parallelkör ekvidisztanciája miatt:

ahol c konstans a F_n normálparallelkörön fellépő sugárhajlás. Tehát F_n (¹0°) esetén:

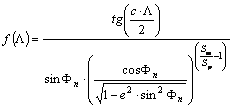
Írjuk fel a h(F=F_n) parallelkör menti hossztorzulást az f(L) g -ba való visszahelyettesítése után:

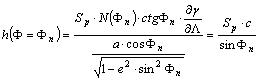
Ebből számítható S_p:

,

illetve adott S_p esetén a c:

.

E vetületet – „módosított rektanguláris polikónikus vetület” néven – F_n=80° választással Bousfield kanadai térképész alkotta meg 1950-ben szerkesztés útján, Kanada 80° szélességi körtől É-ra fekvő területeinek geokartográfiai ábrázolására. A vetületi egyenleteket Haines kanadai geodéta publikálta 1981-ben. A konstansok megválasztásánál az volt a cél, hogy a vetület illeszkedjen a Kanada 80° szélességtől D-re fekvő területeinek vetületéhez. Ez a Lambert-Gauss féle szögtartó kúpvetület F₁=49°, F₂=77° normálparallelkörökkel, melynek n sugárhajlása: n=0.90079. A módosított polikónikus vetület F_n=80° normálparallelkörén előírt c konstanst ezzel egyenlőnek választjuk: c=n=0.90079. A fenti Lambert-Gauss kúpvetületben h(F=80°)=1.0211, a középmeridián (92° Ny) menti hossztorzulás tehát akkor lesz folytonos, ha S_m=1.0211. Végül a fenti képletből S_p=1.1164.

Geokartográfiai világtérképművek vetületei

Az 1 : 1 000 000 méretarányú nemzetközi világtérképmű vetülete

Penck, a kiváló német földrajztudós az 1891-es berni nemzetközi földrajzi kongresszuson vetette fel egy nemzetközi együttműködésben elkészítendő 1 : 1 000 000 méretarányú földrajzi világtérképmű (Internationale Weltkarte IWK, International Map of the World IMW) gondolatát. Az 1909-es londoni kongresszuson eldőlt, hogy a Földet a szélességtől függően 4°x6°-os, 4°x12°-os és 4°x24°-os szelvényeken jelenítik meg, egyszerű polikónikus vetületben. Lallemand francia geodéta 1911-re dolgozta ki a módosított polikónikus vetület részletes leírását, amely 1962-ig a világtérképmű hivatalosan elfogadott vetülete lett.

A módosított polikónikus vetületben a Clarke (1880) ellipszoid alakúnak tekintett Földet foktrapézokra bontják, és ezeket külön-külön képezík le síkba. A foktrapézok mérete:

· -60° és 60° között szélességben 4°, hosszúságban 6°;

· ±60° és ±76° között szélességben 4°, hosszúságban 12°;

· ±76° és ±84° között szélességben 4°, hosszúságban 24°.

A grafikus szerkeszthetőség követelményeinek megfelelően a szélességi körök körívekre, a hosszúsági körök egyenes szakaszokra képeződnek le. A szélességi körök r sugara a polikónikus vetület előírása szerint:

.

A két határoló parallelkör hossztartó. Ugyancsak hossztartók a középmeridiántól

· ±2°-ra elhelyezkedő meridiánok -60° és 60° között ;

· ±4°-ra elhelyezkedő meridiánok ±60° és ±76° között;

· ±8°-ra elhelyezkedő meridiánok ±76° és ±84° között.

A síkkoordinátarendszert a poliéder-rendszerű vetületekhez hasonlóan szelvényenként vesszük fel. Kerüljön az y koordinátatengely a L₀ hosszúságú középmeridiánra, az x pedig érintse az egyik (É-i félgömbön fekvő szelvény esetén a D-i) határoló parallelkört (???ábra). A vetületi koordináták – a leképezés szerkesztés-központúsága miatt – egy algoritmussal adhatók meg, amelyet Snyder amerikai kartográfus dolgozott ki. Ennek leírásához kiindulásul felhasználjuk az egyszerű polikónikus vetület egyenleteit, amelyek érvényesek a határoló F₁ és F₂ parallelkörökre azok hossztartása miatt, eltekintve az y vetületi egyenlet első tagjától, amely a parallelkörök képének távolságát adja meg a középmeridián mentén, és amelyet itt egyelőre nem ismerünk. Tehát helyettesítsük az egyszerű polikónikus vetület y vetületi egyenletében a 4°-nyi középmeridián-rész térképi hosszát megadó

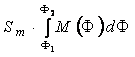
tagját a t₂ ismeretlennel (megjegyezve, hogy a F₁ és F₂ parallelkörök hossztartása miatt S_p=1):

és

.

Tekintsük most az egyik L_h hossztartó meridiánnak a térképszelvényünkbe eső részét, és jelöljük a végpontok koordinátáit x₁, y₁-gyel ill. x₂, y₂-vel (???ábra). A fenti egyenletekből:

és

.

Itt a t₂ még nem ismert, ezért y₂-t sem ismerjük.

Másrészről viszont a meridián hossztartása miatt a térképi szakasz Pythagorász-tételből adódó hossza megegyezik az alapfelületi hosszal:

Ebben az egyenletben csak y₂ ismeretlen, amely kifejezhető és kiszámítható; ezt visszahelyettesítve a vetületi egyenlet bal oldalába, onnan t₂ is kijön.

Vegyük most a L_h hossztartó meridiánnak egy tetszőleges F szélességű pontját (F₁<F<F₂); e pont síkkoordinátáit jelölje x_h, y_h. A meridiánkép megfelelő szakaszait egy-egy derékszögű háromszög átfogóinak tekintve, a koordinátakülönbségekre mint befogókra a hasonló derékszögű háromszögekből az alábbi egyenlőség adódik:

Másrészt a L_h meridián hossztartása miatt

Fejezzük ki az első egyenletből pl. (x_h-x₁) –et, és helyettesítsük a másodikba. Ekkor a második egyenletből y_h kifejezhető és kiszámítható, majd ezt az első egyenletbe visszahelyettesítve, x_h-t is megkapjuk.

Szükségünk lesz a F szélességi kör y tengellyel alkotott metszéspontjának az origótól mért t távolságára. E parallelkör képének r(F) sugara:

Az (y_h–t) távolságot írjuk fel a r(F) rádiuszvektorhoz mint átfogóhoz tartozó befogók segítségével:

Az ismert x_h, y_h segítségével innen t kiszámítható.

Térjünk át egy tetszőleges L hosszúsági kör képén elhelyezkedő pontok koordinátáinak kiszámítására. E meridián képe egyenes szakasz, melynek végpontjai a hossztartó határoló szélességi körökön vannak; jelöljük koordinátáikat F=F₁ esetén x₃, y₃-mal, F=F₂ esetén x₄, y₄-gyel. A fenti analógia szerint

és

.

Az általános helyzetű, F, L koordinátájú pont síkkoordinátáit jelölje x, y. Tekintsük a meridiánkép megfelelő szakaszait itt is egy-egy derékszögű háromszög átfogójának. A koordinátakülönbségeket mint befogókat itt is egy aránypár kacsolja össze:

Másrészt az (y-t) távolságot a fentiekhez hasonló módon írjuk fel az x, y koordináták mint befogók által alkotott derékszögű háromszög segítségével:

A két utóbbi egyenletből x és y már kiszámítható.

A módosított polikónikus vetület általános torzulású. Az egyes szelvényeket határoló parallelkörök hossztartók ugyan, de nem torzulásmentesek: a meridiánképek a határoló parallelkörök képeit (a középmeridián kivételével) nem derékszögben metszik. Emiatt a négy szomszédos szelvény nem mindig illeszthető össze hézagmentesen (???ábra).

1962 után e világtérképmű szelvényeinek készítésénél a Lambert-Gauss féle szögtartó kúpvetület alkalmazására tértek át.

Az 1 : 2 500 000 méretarányú nemzetközi világtérképmű vetülete

Az 1 : 2 500 000 méretarányú, elsősorban geokartográfiai célokra készült világtérképmű (7"DH" ;4D", World Map) gondolata a 60-as években merült fel a szocialista országokban, az 1 : 1 000 000 méretarányú nemzetközi világtérképmű kiadásának akadozása miatt. A 244 szelvény a szocialista országok együttműködésében készült el. A térképmű vetületét Ginzburg szovjet kartográfus dolgozta ki. Alapfelületként a nemzetközi Kraszovszkij ellipszoidot választotta.

Mindkét félgömb három-három gömbövre való felosztása után ezek külön-külön képeződnek síkba: a pólusoknak a ±60°-os szélességekig terjedő környezete ekvidisztáns síkvetülettel, az egyenlítőtől a ±24°-os szélességekig egy-egy meridiánban hossztartó kúpvetülettel, a ±24° és a ±64° közötti gömböveken pedig szintén meridiánban hossztartó kúpvetülettel (ld.???ábra). A vetületi egyenleteket a sík- és kúpvetületek szokásos (és a korábbiakban általunk is követett) tárgyalásától eltérően nem a B pólustávolság, hanem a F szélesség függvényében adják meg. A függőleges koordinátatengelyt x-szel, a vízszintest y-nal jelölik.

ahol a r sugárfüggvény:

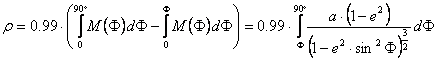
A térképen a kezdőmeridián a pólus x tengelyen elhelyezkedő képétől az origóig húzódik, az y koordinátatengely a határoló szélességi kört alul érinti.

A meridiánok mentén a hossztorzulás 0.99-szeres. A vetület hossztartó parallelköre a 76° szélesség közelében, pontosabban a 75.943202°º75°56’35.53” szélességen van, amely így torzulásmentes; ettől a pólus felé a parallelkörök mentén a hosszak rövidülnek, ezen kívül növekednek. A hossztorzulások 1-től való eltérése a sarkkörön belül nem haladja meg a 2%-ot; a területtorzulások gyakorlatilag az egész területen az egység ±2%-os környezetén belül maradnak.

A kúpvetület első sávjai, mint már említettük, a ±24° és a ±64° közé esnek. (±60° és ±64° között ezért átfedés van a síkvetületi és a kúpvetületi sávok között.) A vetületi egyenletek:

ahol az n sugárhajlást az

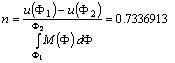
képlet adja, ahol F₁=±32°, F₂=±64° a két hossztartó parallelkör, u(F₁) és u(F₂) ezek alapfelületi sugara. A r sugárfüggvény:

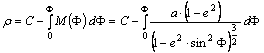
ahol C az egyenlítő térképi sugara:

A ±50°-os szélességen mintegy 4%-os hossz- és területcsökkenés, a ±24°-os parallelkörön 4%-os hossz- és területnagyobbodás lép fel.

A kúpvetület második sávjait az egyenlítő és a ±24°-os szélességi körök határolják. A vetületi egyenletek és a vetületi konstansok képletei megegyeznek az első sávnál látottakkal. A hossztartó parallelkörök: F₁=±4° és F₂=±21°. Innen kiszámítható, hogy

és

Ebben a sávban a hossz- és területtorzulás 1-től való eltérése csak az egyenlítőn haladja meg kis mértékben az 1%-ot.

Az w maximális iránytorzulás értéke a térképrendszer nagy részén 1° alatt marad, és csak az egyes vetületek határterületén emelkedi 2° fölé.