Valódi kúpvetületek
Valódi
kúpvetületeknek azokat a leképezéseket nevezzük, amelyek fokhálózata (vagy
segédfokhálózata) rendelkezik az alábbi tulajdonságokkal:
- a
(segéd-) parallelkörök képei koncentrikus
körívek,
- a
(segéd-) meridiánok képei egy pontba
összetartó egyenesek, és
- a
(segéd-) parallelkörök képei mindenütt merőlegesen
metszik a (segéd-) meridiánok képeit; - továbbá megköveteljük, hogy a
(segéd-) meridiánok által az alapfelületen bezárt Dl szög és az ennek megfelelő
képfelületi Dl’ szög legyen mindig arányos.
Ezt a kúpvetületet jellemző
![]()
arányt,
melynek értéke a gyakorlatban 0<n<1,
sugárhajlásnak nevezzük.
A
valódi kúpvetületeknél a fenti első tulajdonság miatt fennáll a zenitálisság. A térképi
polárkoordináta-rendszer origója a meridián-egyenesek közös pontja, tengelye a
középmeridián, amely az egyszerűség kedvéért legyen egyben kezdőmeridián. A
polártávolságot a parallelkörök térképi sugara, a r sugárfüggvény,
a polárszöget a l'=n×l szög adja meg. Ebből a derékszögű
síkkoordinátákat az
![]()
vetületi
egyenletekkel írhatjuk fel. A kezdőmeridián itt is az y tengely negatív felével esik egybe. (Ha az y
tengelyt a kezdőmeridiántól különböző l0 középmeridiánra akarjuk illeszteni, akkor a hosszúságkülönbség Dl=l-l0 jelölésével a vetületi
egyenletek
![]()
![]()
alakúak.)
A
sugárfüggvény és a sugárhajlás tehát lényegében meghatározza a valódi
kúpvetületet, ezekből a vetület minden tulajdonsága levezethető. Hasonlóan a
valódi síkvetületekhez, a r sugárfüggvényt itt is
a pólustávolság
függvényében adjuk meg: r=r(b), mely az egyrétűség miatt szigorúan monoton növő függvény.
Ha r(0)=0, vagyis a (segéd-)
meridiánok képei egy pontban találkoznak, amely a (segéd-) pólus képe, akkor póluspontos kúpvetületről beszélünk. A pólusvonalas kúpvetületeknél r(0)>0, vagyis a (segéd-) pólus
képe egy körív, melyben a meridiánképek végződnek; ekkor viszont ezek
meghosszabbításai találkoznak egy pontban. Egy pólus-középpontú gömbsüveg képe
kúpvetületben tehát vagy körcikk (póluspontosnál), vagy körgyűrű-cikk
(pólusvonalasnál). Jelöljük a körcikk vagy körgyűrű-cikk nyílásszögét w-val (??? ábra). Az n sugárhajlás felírható
![]() alakban;
alakban;
innen
következik, hogy
![]() ill.
ill. ![]() .
.
A
fokhálózat menti torzulások:
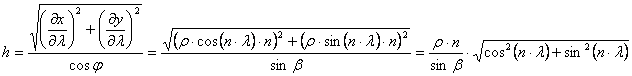
tehát
![]()
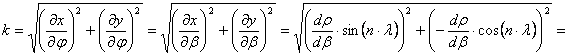
![]()
azaz
![]()
Látható,
hogy mindkét hossztorzulás független l-tól.
A térképi
fokhálózat merőleges (Q=90°), vagyis a fokhálózati
vonalak vetületi főirányok. Az a és b extremális hossztorzulások közül az
egyik h-val, a másik k-val fog megegyezni, amelyekből adódik
a területi modulus:
![]()
illetve
a térkép valamely pontjában fellépő 2×DImax maximális szögtorzulás.
Valódi
kúpvetületben ritkán ábrázolnak félgömbnyi vagy annál nagyobb területet. A
geokartográfiában többnyire a pólustól és az egyenlítőtől egyaránt távolabb
fekvő területek: kontinensek, kontinensrészek vagy országok ábrázolására
használják. Előfordul nagyobb méretarányú (topográfiai vagy navigációs)
térképek vetületeként, ellipszoid alapfelülettel is.
A
valódi kúpvetületek közül először a perspektív kúpvetületeket vesszük sorra.
Perspektív kúpvetület – metsző változat
Vegyünk
fel egy, a K csúcspontban 2×e nyílásszögű forgáskúp-palástot, amely két
parallelkörben metszi az alapfelületet. Jelöljük az O gömbközéppont és a Q
vetítési középpont távolságát f-fel,
a QK távolságot c-vel. (Az egyrétűség miatt legyen ½f ½£1.) Legyen S a b pólustávolságú alapfelületi
P pontból, T pedig a képfelületi P’ pontból a forgástengelyre bocsátott
merőleges talppontja; végül a KP’ távolság éppen a r sugárfüggvény (???ábra).
A
QTP’ és a QSP derékszögű háromszögek hasonlók, ezért a befogóikra teljesül:
![]()
Vegyük
észre, hogy TP’=r×sine, SP=sinb és QS=f+cosb, továbbá TK=r×cose. Elvégezve a behelyettesítéseket, kapjuk,
hogy
![]()
Bontsuk
fel a c=QK távolságot a T ponttal két részre:
![]()
Innen
kifejezhető a r sugárfüggvény:
![]()
Az n sugárhajlás meghatározásához terítsük
ki a P’ ponton átmenő parallelkör-kép által határolt kúppalástot egy körcikké,
melynek nyílásszögét jelöljük w-val (???ábra). A
sugárhajlás definíciójából:
![]()
(Felhasználtuk,
hogy a körcikket határoló – r sugarú – körív hossza egyrészt megegyezik a
kúppalást r×sine sugarú alapkörének
kerületével, másrészt a körív hossza úgy aránylik a r sugarú kör kerületéhez, mint ahogy w aránylik a teljes szöghöz.)
A
fokhálózat menti hossztorzulások:
![]()
![]()
Az
összevonások után
![]()
A
hossztorzulások a ???ábrán láthatók. Mivel h¹k és h¹1/k, vagyis a perspektív kúpvetület
általános torzulású. A h számlálójában ill. nevezőjében
szereplő tényezők megjelennek a k
számlálójában ill. nevezőjében is; ebből adódóan elsősorban a területtorzulások
megnövekedésével kell számolni, míg a szögtorzulások mérsékeltebbek. A metszési
parallelkörökön h¹1, de k¹1, ezért ezek bár hossztartók, de nem
torzulásmentesek. A t területtorzulási modulust
és a maximális w iránytorzulást jellemző
mutatószámot az ismert képletekből h és
k segítségével számíthatjuk ki.
Perspektív kúpvetület – érintő változat
Az
érintő perspektív kúpvetület a metsző változat határhelyzete, midőn a két
metszési parallelkör egybeesik; tehát az ott elmondottak az érintő változatra
is teljesülnek. Érintse a kúp a gömb alapfelületet a bn pólustávolságú
parallelkörön. A ???ábrán látható, hogy a
bn szög és a kúp e fél nyílásszöge egymás
pótszögei:
![]()
Az n sugárhajlás ennek felhasználásával:
![]()
A bn pólustávolságú érintő parallelkör rn sugárfüggvénye az ábra alapján:
![]()
A bn érintési parallelkörön nincs hossztorzulás (h=1); másrészt behelyettesítve a
fokhálózat menti hossztorzulásokba:
![]() ,
,
amiből
az érintési parallelkör torzulásmentessége következik.
Ezek
a tulajdonságok – más tartalommal – a nem-perspektív kúpvetületeknél is meg
fognak jelenni.
Parallelkörökben hossztartó (ortografikus)
kúpvetület
Vizsgáljuk
a perspektív kúpvetületet f®¥ esetén. Bontsuk fel ehhez a
c távolságot az O ponttal két részre:
![]()
A r sugárfüggvény:
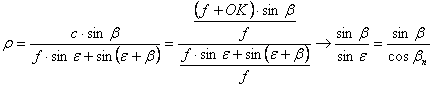
(Itt
felhasználtuk, hogy a végtelenből jövő párhuzamos vetítősugarak esetén a
kúppalást-képfelület önmagával párhuzamosan tetszőlegesen eltolható a térkép
változása nélkül; ekkor választhatjuk az érintő változatot, és jelöljük az
érintési parallelkört bn-nel, ami a fentiek szerint e pótszöge, ezért sine=cosbn.)
A
fokhálózat menti torzulások:
![]()
vagyis
ez a kúpvetület valóban parallelkörökben hossztartó.
![]()
A bn parallelkörön k=1, tehát az érintési parallelkör itt
is torzulásmentes.
Áttérünk
most a gyakorlati szempontból fontosabb nem-perspektív valódi kúpvetületek
tárgyalására.
Meridiánokban hossztartó valódi kúpvetületek
A
meridiánokban való hossztartásból k=1 következik, tehát
![]() , vagyis
, vagyis ![]()
A d integrációs konstans megválasztásától
függően három különböző valódi kúpvetületet kapunk.
a)
Póluspontos, meridiánban hossztartó
valódi kúpvetület
A
póluspontosság azt jelenti, hogy a pólus sugara zérus. Ez képletben: r(b=0)=0. Ez a r=arcb+d sugárfüggvény estén akkor
teljesül, ha d=0, vagyis
![]()
A h
parallelkör menti hossztorzulás ekkor
![]()
Ez b függvényében szigorúan monoton nő, b®180° esetén h®¥, és n<1
miatt a pólusban h<1 (???ábra).
A vetületnek emiatt mindig van egy és csak egy bn hossztartó parallelköre. Vezessük be a rn=r(bn)=arcbn jelölést. A hossztartás miatt e parallelkör
hossza az alapfelületen (és a képfelületen is): 2×p×sinbn. A képfelületen ez egy w középponti szöghöz tartozó, rn sugarú körív, mely úgy aránylik a rn sugarú kör kerületéhez, mint w a teljes szöghöz. Ebből megkapjuk az n
sugárhajlást:
![]()
Most
már felírhatók és grafikusan ábrázolhatók (ld. ábra) a fokhálózat menti
hossztorzulások:
![]()
és
![]() .
.
Vetületünk
tehát általános torzulású. A bn hossztartó parallelkör torzulásmentes.
Ez
a vetület a geokartográfiai gyakorlatban ritkán fordul elő.
b)
Pólusvonalas, meridiánban hossztartó
valódi kúpvetület egy hossztartó parallelkörrel (Ptolemaios 1. vetülete)
k=1 miatt r=arcb+d, és a pólusvonalasságból
adódóan d>0. Válasszuk a bn parallelkört
hossztartónak, ekkor rn=arcbn+d;
ebből d= rn-arcbn, vagyis
![]()
Másrészt
a hossztartás miatt a parallelkör képi hossza az w nyílásszögű körgyűrű-cikken
megegyezik az alapfelületi hosszal:
![]()
Ebből
felírható n:
![]()
majd
a parallelkör menti h hossztorzulás:
![]()
Hátra
van még a fenti egyenlőségekben szereplő, egyelőre ismeretlen rn konstans meghatározása. Ez
azon a megfontoláson alapszik, hogy a b=0° és b=180° esetén a ¥-hez tartó, ezek között
pedig egyetlen minimummal rendelkező h=h(b) függvénynek a hossztartó bn szélességnél kell legyen a
minimuma, ellenkező esetben ugyanis nem egy, hanem két hossztartó parallelkör
volna. A h=h(b) függvény minimuma a
derivált zérushelyénél található, tehát:
![]()
Deriváljuk a fenti h-t:
![]()
Ennek
a b=bn-ben vett helyettesítési
értéke tehát zérus:
![]()
A
számláló csak akkor lehet zérus, ha
![]()
azaz ![]()
(Ez
megegyezik az érintő perspektív kúpvetület normálparallelkörének sugarával.)
Ennek
felhasználásával a sugárfüggvény:
![]()
A
sugárhajlás:
![]()
Ez
az érték megegyezik az érintő perspektív kúpvetület sugárhajlásával.
Következésképpen ha egy pólus középpontú gömbsüveg képét (egy körgyűrű-cikket)
forgáskúp-palásttá hajtunk össze, akkor ez elhelyezhető
úgy az alapfelülethez képest, hogy éppen a normálparallelkör mentén
érintsék egymást.
A
parallelkör menti h hossztorzulás:
![]()
és
a meridián menti k hossztorzulás természetesen:
k=1
Ebből
adódóan ez a vetület általános torzulású. A bn hossztartó szélességi kör
torzulásmentes.
A
fokhálózat menti torzulások menetét a ???. ábra grafikusan mutatja be.
Ptolemaios
(Kr.u. II.sz.) "Geographika" c. művében adja meg e vetület szerkesztését,
és az ő térképeinél találkozunk e
vetület legkorábbi alkalmazásával. Egyszerű, könnyen szerkeszthető fokhálózatú
vetület, amelyet a geokartográfiában kontinensrészek, országok ábrázolásához
alkalmaznak.
c) Meridiánban és két
parallelkörben hossztartó valódi kúpvetület (de l'Isle vetülete)
k=1 miatt továbbra is r=arcb+d, ahol d>0 a pólusvonal sugara, vezessük tehát be a rp=d jelölést:
![]()
Határozzuk
meg most rp-t és n-et
a két hossztartó pólustávolság függvényében. Ha b1, b2 jelöli a hossztartó parallelköröket, akkor a
hossztartásból a
![]()
![]()
egyenletek
adódnak. Vonjuk ezeket ki egymásból, és vegyük figyelembe a meridián menti
hossztartást:
![]()
Ebből
az n sugárhajlás kifejezhető:
![]()
Fejezzük
ki most n-et a hossztartás fenti
egyenleteiből is:
![]()
vagyis
![]()
Az
utolsó egyenlőséget átrendezve:
![]()
Innen
rp kifejezhető:
![]()
A
parallelkör menti h hossztorzulás:
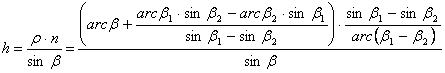
Ez
továbbra sem egyenlő 1-gyel, ezért ez a vetület is általános torzulású.
A
két normálparallelkör (b1 és b2) k=1 miatt torzulásmentes.
De
l'Isle vetületének alkotó függvényei más formában is felírhatóak, amelyek néha
előnyösebbek a fentieknél. Ehhez vezessük be a hossztartó parallelkörök
pólustávolságának középértékére a
![]() ,
,
továbbá
a
![]()
jelölést.
Jelöljük bk gömbi
távolságát a hossztartó parallelköröktől ek-val:
![]()
A meridián
menti hossztartás miatt
![]() és
és ![]() .
.
Írjuk
fel a hossztartó parallelkörök alap- és képfelületi hosszának egyenlőségét:
![]()
![]()
Az
összegezést és az egyszerűsítést elvégezve, majd az egyenleteket egymásból
kivonva kapjuk, hogy
![]()
ahonnan
![]()
Adjuk
most össze a parallelkörök hossztartásának fenti egyenleteit. Ebből kapjuk,
hogy
![]()
Kifejezzük
rk-t:
![]()
A r sugárfüggvény ekkor a
következő alakot ölti:
![]()
Ez
a vetület J. N. de l'Isle francia csillagásztól származik (1745), aki
Oroszország ábrázolásához készítette. A torzulási viszonyok egy, a hossztartó
parallelköröket is magába foglaló, széles sávban igen kedvezőek. Közepes
szélességen fekvő országok, kontinensrészek, kontinensek általános torzulású
ábrázolásához manapság ez a legelterjedtebben használt vetület.
Szögtartó kúpvetületek
A
szögtartás alapegyenlete: a=b=h=k, ami figyelembe véve, hogy a
valódi kúpvetületeknél
![]() és
és ![]() ,
,
az
alábbi egyenletet adja:
![]()
Ez
szétválasztható változójú, melyet a szokásos módon alakítunk át:
![]()
Ennek
a megoldása:
![]()
ahol
ln d-vel jelöltük az integrációs konstanst (d>0).
Mindkét
oldalt az exponenciális függvény kitevőjeként véve, kapjuk a sugárfüggvényt:
![]()
A
sugárfüggvény mutatja, hogy a szögtartó kúpvetület póluspontos, de a kúpvetület
alaptulajdonságából (0<n<1) adódik, hogy a póluspontban a szögtartás nem
áll fenn. A vetület további tulajdonságait az n sugárhajlás mellett a d(>0)
hasonlósági tényező határozza meg, melynek értéke éppen r(b=90°) -kal, vagyis az
egyenlítő térképi sugarával egyezik meg.
A
parallelkör menti h hossztorzulás
(mely az alapegyenlet miatt egyben k-val
is egyenlő):
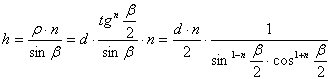
Az
utolsó alak mutatja, hogy b®0° és b®180° esetén h®¥, a kettő között pedig egy
minimuma van. A szögtartó kúpvetület tehát a gyakorlatban vagy egy, vagy két
hossztartó parallelkörrel rendelkezik. A hossztartó parallelkör(ök) viszont a
szögtartás miatt egyben torzulásmentes(ek) is.
A d és az n
meghatározása a vetületek további tulajdonságaiból lehetséges.
A
3000 km-nél nem hosszabb ortodróma-ívek képe az egyenestől alig tér el, ezért a
léginavigáció térképeihez a II. világháború óta leginkább ezt a vetületet
alkalmazzák.
A
szögtartó kúpvetület J. H. Lambert német matematikustól származik (1772).
a) Szögtartó kúpvetület egy hossztartó
parallelkörrel
Ha
egyetlen hossztartó bn parallekör
van, akkor annak éppen a h
minimumhelyének kell lennie. A h-nak
ott lehet minimuma, ahol a deriváltja zérus. Képletben:
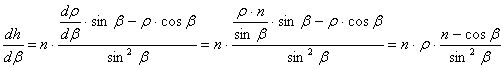
(itt
felhasználtuk az alapegyenletből adódó h=k
egyenlőséget.) Ezt a függvényt a b=bn helyen tegyük zérussál egyenlővé:
![]()
ami
akkor teljesül, ha
![]()
Ez
az egyenlőség azt mutatja, hogy egy
hossztartó parallelkör esetén a sugárhajlás megegyezik az ugyanott érintő
perspektív kúpvetület sugárhajlásával. Tehát, Ptolemaios kúpvetületéhez
hasonlóan, ha egy pólus-középpontú gömbsüveg képeként keletkező körgyűrűt
forgáskúp-palásttá hajtunk össze, akkor az elhelyezhető
úgy, hogy a két felület éppen a hossztartó parallelkör mentén érintse
egymást.
Ezen
tulajdonság alapján tudjuk meghatározni a d
konstans értékét, ugyanis a bn hossztartó
és egyben érintési parallelkör sugárfüggvénye: r(bn)=tgbn., amely meg kell egyezzen a sugárfüggvény bn-ben felvett értékével:
![]()
azaz
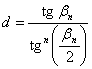
A
hossztartó parallelkör a szögtartás miatt egyben torzulásmentes is. Ettől a
parallelkörtől távolodva mind a hossztorzulás, mind a területtorzulás nő.
Herschel
angol csillagász a szögtartó kúpvetületet a szögtartó (sztereografikus)
síkvetület általánosításaként fogta fel, ahol a
![]()
sugárfüggvény
n=1 esetén éppen az egyenlítőn metsző
sztereografikus síkvetületet adja. A sugárhajlást 240°-nak választva és a
póluskörnyéki területeket eltávolítva, a vetületet térképes lámpaernyő
készítéséhez ajánlotta.
b) Szögtartó kúpvetület két hossztartó
parallelkörrel
Jelöljük
b1.-gyel és b2-vel a hossztartó
parallelköröket. Ezek térképi hossza úgy aránylik egymáshoz, mint az
alapfelületi hosszuk:
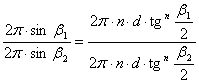
Az
egyszerűsítések és az egyenlet logaritmálása után kapjuk, hogy
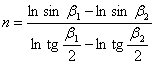
A d konstans meghatározása a hossztartás
egyenleteiből következik:
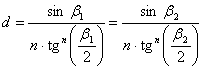
A
hossztartó parallelkörök a szögtartás miatt egyben torzulásmentesek is. A két
normálparallekör között a hosszak és területek csökkennek, ezeken kívül pedig a
távolodással együtt növekednek; a torzulási modulusok 1-től való eltérése egy
sokkal szélesebb övezetben tartható egy küszöbérték alatt, mint az egy
parallelkörben hossztartó változatnál.
Minden
két parallelkörben hossztartó szögtartó kúpvetület egy arányos nagyítással
átvihető egy ugyanolyan sugárhajlású, egy parallelkörben hossztartó változatba;
ugyanez - arányos kicsinyítéssel - fordítva is igaz.
A
vetületet – általában „Lambert féle kúpvetület”, helyenként „Lambert-Gauss
vetület” néven – előnyös torzulási tulajdonságai miatt a mind a geokartográfiában,
mind a topokartográfiában (ellipszoid alapfelülettel) elterjedten használják.
Területtartó kúpvetületek
A
területtartás alapegyenlete: a×b=h×k=1. Ezt alkalmazva a
![]() és
és ![]()
fokhálózat
menti tirzulásokra, kapjuk a
![]()
egyenletet.
Ez is szétválasztható változójú, melyet átalakítva és integrálva:
![]()
Ennek
a megoldása:
![]()
vagyis
![]()
Fejezzük
ki innen a d integrációs konstanst
értelmezés céljából:
![]()
(Itt
használtuk a pólusvonal sugarára a rp=r(b=0) jelölést.) Ezt
visszahelyettesítve r2 képletébe:
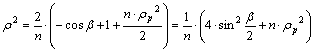
A r sugárfüggvény tehát:
![]()
A rp megválasztásától függően kapjuk a területtartó
kúpvetület különböző változatait.
Vizsgáljuk
meg a parallelkör menti hossztorzulást:
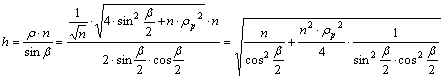
A
gyökjel alatti második tag b®0° esetén, az első és a második tag b®180° esetén ¥-hez tart, a két tag
összegének 0° és 180° között van egy minimuma. A területtartó kúpvetület tehát
vagy egy, vagy két hossztartó parallelkörrel rendelkezhet.
a)
Póluspontos területtartó kúpvetület
A rp pólusvonal hossza most zérus, tehát a
sugárfüggvény:
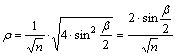
Válasszuk
bn -et hossztartónak, és használjuk a rn=r(bn) jelölést:
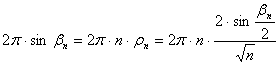
Innen
kifejezhető ![]() :
:
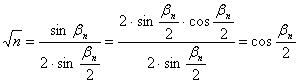
tehát
a sugárhajlás:
![]()
(Ez
nem egyezik meg az érintő perspektív kúpvetület n=cosbn sugárhajlásával, tehát a forgáskúp-palásttá
összetekert körcikk alakú térkép nem helyezhető el úgy, hogy éppen a hossztartó
parallelkörnél érintse az alapfelületet.)
n-et behelyettesítve a sugárfüggvénybe,
kapjuk:
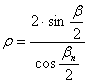
A
fokhálózat menti hossztorzulások:
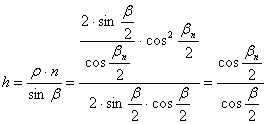
és
a területtartásból
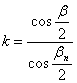
A bn normálparallelkör ezek szerint torzulásmentes.
A
parallelkör menti hossztorzulás szigorúan monoton növő, ezért nincsen két
parallelkörben hossztartó változata.
Ezt
a vetületet is J. H. Lambert készítette.
b) Pólusvonalas területtartó kúpvetület
egy hossztartó parallelkörrel
A
területtartásból adódóan itt is
![]()
Az n sugárhajlás kiszámításához
emlékeztetünk feltételezésünkre, mely szerint egyetlen hossztartó bn parallelkör van. Ez a h általánosabb alakjánál elmondottak miatt akkor állhat elő, ha a
parallelkör menti h hossztorzulás
éppen bn-nél veszi fel a minimumát. Ehhez számoljuk ki a h b szerinti deriváltját :
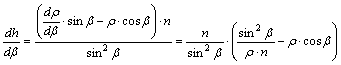
(Itt
felhasználtuk a területtartás alapegyenletét.) Ezt kell a bn helyen zérussá tenni (rn=r(bn) jelöléssel):
![]()
Ez
az egyenlőség akkor teljesül, ha
![]()
vagyis
a minimumfeltétel következménye:
![]()
A bn parallelkör hossztartásából
![]()
Innen
rn-et a fenti egyenletbe behelyettesítve
![]()
az
egyszerűsítések után megkapjuk a sugárhajlást:
![]()
Ez
itt is azt jelenti, hogy a pólus-középpontú gömbsüveg képeként előálló
körgyűrű-cikket forgáskúp-palásttá összehajtva, hozzáérinthető az
alapfelülethez úgy, hogy éppen a normálparallelkörnél érintsék egymást.
A
pólusvonal rp sugarának meghatározásához a fenti
minimumfeltételből adódó egyenletet használjuk fel, a rn2 behelyettesítésével:
![]()
n×rp2-et kifejezve:
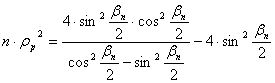
közös
nevezőre hozás után:
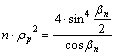
A r sugárfüggvény tehát explicit
alakban
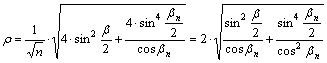
E
vetület fokhálózat menti torzulásai:
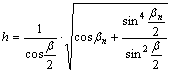
és
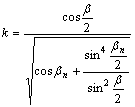
A bn normálparallelkör tehát torzulásmentes.
c) Pólusvonalas területtartó kúpvetület
két hossztartó parallelkörrel
A
sugárfüggvény a területtartásból következőleg továbbra is
![]()
ahol
az n
és a rp konstansokat a b1 és b2 parallelkörök hossztartása determinálja.
Írjuk
fel n kiszámításához a hossztartást
képletben:
![]()
![]()
Fejezzük
ki ezekből a gyököket:
![]()
![]()
Négyzetreemelés
és az alsó egyenlet felsőből történő kivonása után:
![]()
Innen
n kifejezhető:
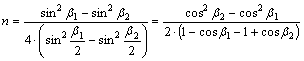
Egyszerűsítve
cosb2-cosb1 -gyel, kapjuk n
végleges alakját:
![]()
Az n×rp2 értéke a
fenti négyzetre emelt egyenletek közül bármelyikből kijön. Vegyük pl. az elsőt:
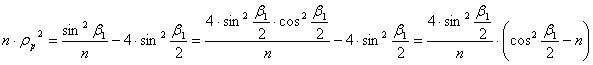
Alakítsuk
át a zárójelben lévő kifejezést:
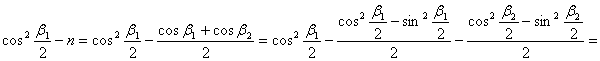
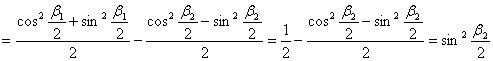
Ezt
visszahelyettesítve n×rp2 –be:
![]()
(Látható,
hogy mind n-ben, mind n×rp2-ben a b1 és b2 helyére bn -et helyettesítve, az egy
parallelkörben hossztartó változat képleteit kapjuk.)
Helyettesítsük
ezt vissza a r sugárfüggvény eredeti
egyenletébe:
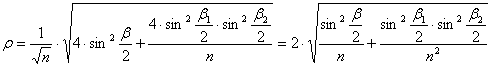
A
fokhálózat menti torzulások:
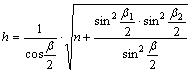
és
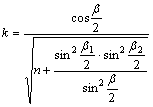
Ez
a vetület Albers német matematikustól származik (1805). Az utóbbi évtizedekben
széles körben használják foktrapéz alakú, K-Ny-i irányban kiterjedt területek
ábrázolásához. Ellipszoid alapfelületű változata az Egyesült Államok nemzeti és
tematikus atlaszainak kedvelt vetülete.