Valódi síkvetületek

Valódi síkvetületeknek azokat a leképezéseket nevezzük, amelyek fokhálózata (vagy segédfokhálózata) rendelkezik az alábbi tulajdonságokkal:

- a (segéd-) parallelkörök képei koncentrikus körök,

- a (segéd-) meridiánok képei egy ponton (a közös középponton) áthaladó egyenesek, és

- a (segéd-) parallelkörök képei mindenütt merőlegesen metszik a (segéd-) meridiánok képeit; - továbbá megköveteljük a (segéd-) pólusban a (segéd-) meridiánok azimutálisságát, vagyis a (segéd-) meridiánok alap- és képfelületi szögeinek azonosságát. A valódi vetületeket ezért szokás azimutális vetületeknek is nevezni.

Ha az alapfelületen egy bizonyos pont mint középpont körüli gömbi körök képei a térképen körívként jelennek meg, zenitálisságról beszélünk. A valódi síkvetületeknél a fenti első tulajdonság miatt tehát fennáll a zenitálisság. Ekkor célszerű a térképen egy polárkoordinátarendszert bevezetni. Egy tetszőleges (j,l) koordinátájú alapfelületi pont képfelületi megfelelőjének polárkoordinátáit a j szélességi kör képének r térképi sugara (az ún. sugárfüggvény) és a l hosszúság mint polárszög adja meg (???ábra). Ebből a derékszögű síkkoordinátákat az

vetületi egyenletek szolgáltatják. A kezdőmeridián itt az y tengely negatív felével esik egybe. Ha az y tengelyt nem a kezdőmeridiánra, hanem a l₀ középmeridiánra akarjuk illeszteni, akkor a hosszúságkülönbség Dl=l-l₀ jelölésével a vetületi egyenletek:

A negatív koordinátaértékek elkerülése céljából a vetületi kezdőpontot a (segéd-) pólusból néha eltolják.

Látható a fentiekből, hogy a valódi síkvetületek vetületi egyenleteit a sugárfüggvény teljes mértékben meghatározza, következésképpen elegendő a sugárfüggvényt ismernünk, ebből a vetület minden tulajdonsága levezethető. Célszerűségi szempontból a r sugárfüggvényt nem a szélesség, hanem a pólustávolság függvényében szokás megadni: r=r(b). Az egyértékű leképezéshez kikötjük r-ról egyrészt, hogy legyen szigorúan monoton növő függvény, másrészt gyakorlati szempontból teljesüljön r(0)=0. Ez utóbbi feltétel miatt a pólus képe egyetlen pont lesz, tehát a pólus környéke a térképen összefüggően jelenik meg.

A fokhálózat menti torzulások:

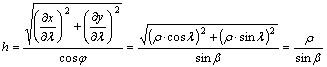
A térképi fokhálózat merőlegessége (Q=90°) miatt a fokhálózati vonalak vetületi főirányok, ezért az a és b extremális hossztorzulások közül az egyik h-val, a másik k-val fog megegyezni. Ezekből kapható meg a területi modulus:

illetve a térkép valamely pontjában fellépő 2×D^I_max maximális szögtorzulás.

Megjegyezzük, hogy ha bármely síkvetületnél a pólusban a k meridián menti hossztorzulás egységnyi, akkor e vetületnek a pólusban nincsen torzulása. Ha ugyanis b®0 esetén

akkor itt a póluspontosság követelménye miatt r®arcb. Ebben az esetben viszont

.

(Az utolsó konvergenciánál felhasználtuk azt az ismert határértékrelációt, hogy x®0 esetén

.)

A pólusban tehát h is tart 1-hez, következésképpen itt t=h×k®1 és 2×D^I_max®0 , ami a lokális területtartást és szögtartást jelenti.

A valódi síkvetületek közül először a perspektív síkvetületeket tárgyaljuk.

Perspektív síkvetületek

A perspektív síkvetület sugárfüggvényét, ezen keresztül pedig a tulajdonságait lényegében az szabja meg, hogy milyen a vetítési középpontnak az alapfelülethez és a képsíkhoz való viszonya. Jelöljük az alapfelület forgástengelyén elhelyezkedő Q vetítési középpont és az alapfelület (jelen esetben a gömb) O középpontjának távolságát f-fel, a vetítési középpont és a képsík távolságát c-vel (???ábra). Világos, hogy önmagában a c változtatása a képsík hasonlósági transzformációját eredményezi, tehát a vetületi torzulások eloszlását elsősorban az f nagysága befolyásolja.

A K vetületi kezdőpont – a térképi síkkoordináta-rendszer origója – kerüljön a képsík és a forgástengely metszéspontjába. Jelöljük a b pólustávolságú alapfelületi P pont képét P’-vel, a P-ből a forgástengelyre bocsátott merőleges talppontját T-vel. Ekkor az ezek által alkotott QTP és QKP’ hasonló háromszögek megfelelő befogóinak arányára kapjuk, hogy:

ahol a fentiek miatt QK=c, QT=f+cosb, TP=sinb .

Jelöljük a két háromszög Q-nál lévő közös szögét e-nal, és a KP’ távolságot r-val. A QKP’ háromszögből:

,

másrészt a QTP háromszögből

Elvégezve a behelyettesítést, kapjuk a r sugárfüggvényre:

Irányítsuk úgy a képfelületen a derékszögű síkkoordinátarendszert, hogy a kezdőmeridián képe az y tengely negatív felével essen egybe. Ekkor a perspektív vetületek általános vetületi egyenletei:

A fokhálózat menti hossztorzulások:

Az f és c paraméterek végtelen sokféleképpen választhatók meg, ezek közül a gyakorlatban három vetület: a sztereografikus, a gnomonikus és az ortografikus bír jelentőséggel.

Perspektív síkvetület nem lehet meridiánban hossztartó, mert a

egyenlőséghez c és f nem választható meg úgy, hogy az egyenlőség b-tól független azonosság legyen. Hasonlóképpen látható, hogy perspektív síkvetület területtartó sem lehet, mert a

vagyis a

egyenlethez szintén nem létezik olyan c és f, amelynél az egyenlőség tetszőleges b-ra fennállna.

Ferdetengelyű és transzverzális perspektív síkvetületek

Vizsgáljunk egy ferdetengelyű perspektív síkvetületet. (???ábra). A normális esethez hasonlóan kapjuk a r sugárfüggvényt a b^* függvényében:

Irányítsuk úgy a képfelületen a derékszögű síkkoordinátarendszert, hogy a kezdő-segédmeridián képe az y tengely negatív felével essen egybe. Ekkor a ferdetengelyű perspektív vetületek általános vetületi egyenletei:

Az NN^* P polárgömbháromszögből az oldal-koszinusztétel szerint

(b₀ az N^* segédpólus – a vetületi kezdőpont – pólustávolsága.)˝A szinusztétel szerint

,

ezt átrendezve:

Behelyettesítve x-be:

A második alapformából és a szinusztételből kapható, hogy

Behelyettesítve y-ba:

Így megkaptuk a ferdetengelyű perspektív síkvetület vetületi egyenleteit a b és l függvényében.

Ezekből b₀ helyére 90°-ot helyettesítve kijönnek a transzverzális elhelyezés vetületi egyenletei:

a) Sztereografikus síkvetület (érintő változat) (f=1, c=2)

A vetítés középpontja tehát a gömb felületén van, a képsík az ezzel átellenes felületi pontban érinti a gömböt (?ábra). A r sugárfüggvény:

Az egyenlítő térképi sugara: r(90°)=2. A teljes Föld egyidejűleg nem képezhető le, mert a vetítési centrumnak választott pólus (b=180°) és környezete a térképen nem ábrázolható.

A fokhálózat menti hossztorzulások:

A hossztorzulásokat szemléltető ???ábra mutatja, hogy hºk, tehát a sztereografikus vetület szögtartó. A grafikonon az is látható, hogy a vetületi kezdőpont torzulásmentes; a pólustól távolodva a hossztorzulási modulusok nőnek, emiatt a szomszédos parallelkörök távolsága is növekszik. A területtorzulási modulus:

Az egyenlítőn (b=90°) a hossztorzulás kétszeres, a területtorzulás négyszeres, ezért e vetületben félgömbnél nagyobb területet ritkán ábrázolnak.

A sztereografikus vetület másik fontos tulajdonsága a körtartás: minden alapfelületi körív képe a térképen is körív lesz (kivéve az egyenesre leképeződő meridiánokat). A síkbeli polárkoordinátarendszerben egy origócentrikus, d sugarú körvonal egyenlete:

és

(ahol r a polártávolság és d a polárszög). Ha a d sugarú kör középpontja valahol a polártengelyen fekszik az origótól r₀ távolságra, akkor a síkháromszögekre vonatkozó koszinusz-tétel alapján

Ebből felírható a kör síkbeli polárkoordinátás egyenlete:

ahol E=-2×r₀ és F=r₀²-d² konstans. A körtartáshoz azt kell belátnunk, hogy az alapfelületi kör sztereografikus vetülete ilyen alakra hozható.

Írjuk fel először a P₀(b₀,l ₀) középpontú gömbi kiskör felületi polárkoordinátás egyenletét (???ábra). Tekintsük ehhez a kör kerületének tetszőleges P(b,l) pontját. Az NP₀P polárgömbháromszög r =P₀P oldala tehát a kör gömbfelületi sugara, az NP oldal a polártávolság, a P₀NP a polárszög. A P₀P oldalra felírva az oldal-koszinusztételt:

A kör középpontjának b₀ koordinátája rögzített. Vezessük be a fenti egyenlet konstansaira az A=cosb₀, B=sinb₀, D=cosr jelöléseket.

Vezessük be b helyett a b/2 szögfüggvényeit:

Osszuk végig az egyenletet cos²(b/2)-lel:

Felhasználva a

egyenlőséget, kapjuk a gömbi kiskör felületi polárkoordinátás egyenletét:

Képezzük le most a síkra ezt a kört normális sztereografikus vetülettel. Az NP₀P polárgömbháromszög képe az N’P₀’P’ idom, melynek N’P’ és N’P₀’ oldala meridián képe, így rendre

és

hosszúságú egyenesek, amelyek által bezárt szög az azimutálisság miatt (l-l₀). A leképezést a

helyettesítéssel végrehajtva:

Elvégezve az összevonásokat:

Osszunk végig a másodfokú tag együtthatójával:

Egy olyan síkbeli polárkoordinátarendszerben, amelyben r a polártávolság és l-l₀ a polárszög, továbbá

,

ez éppen egy síkbeli kör polárkoordinátás egyenlete, amivel a sztereografikus leképezés körtartó voltát beláttuk.

A körtartási tulajdonság a fokhálózat szerkesztését megkönnyíti; ennek főleg transzverzális és ferdetengelyű elhelyezésnél van – illetve volt a számítógépes rajzoltatás elterjedése előtt – jelentősége.

A sztereografikus vetület metsző (és külső elhelyezésű) változatai

A c paraméter értékének megváltoztatásával az érintő elhelyezésű sztereografikus vetületből c<2 esetén metsző, c>2 esetén külső elhelyezésű variánst kapunk. A c paraméter megváltoztatása ugyanakkor a sztereografikus vetület szögtartását és körtartását nem befolyásolja.

A metsző variánst példázza az Országos Meteorológiai Szolgálat által 1983 óta rendszeresített, a 60°-os szélességi körön metsző sztereografikus vetület. A metszési parallelkör szélességének megfelelően c=1+sin60°, tehát a r sugárfüggvény:

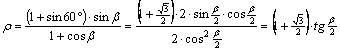
A hossztorzulás:

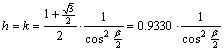
A 60°-os szélességi kör torzulásmentes. Ezen kívül a hosszak és a területek növekednek, ezen belül csökkennek. A vetületi kezdőpontban a hossztorzulás: h=k=0.9330.

Az iménti állítás meg is fordítható: a szögtartó síkvetületek mind azonosíthatók egy megfelelő c-hez tartozó sztereografikus vetülettel. Vegyünk ugyanis egy tetszőleges szögtartó síkvetületet. Ennek r sugárfüggvényére teljesülnie kell a

vagyis a

egyenletnek. Átrendezve és integrálva:

Elvégezve az integrálást:

Kifejezve a r sugárfüggvényt:

ahol a c=exp(d) szám bármilyen pozitív értéket felvehet. Ezzel beláttuk, hogy a sztereografikus síkvetületeken kívül nincsen más szögtartó síkvetület, vagyis a sztereografikus síkvetületek halmaza megegyezik a szögtartó síkvetületek halmazával.

A sztereografikus síkvetületet normális elhelyezésben elsősorban a pólus környékének ábrázolására használják; félgömbnél nagyobb terület ábrázolása a gyorsan növekvő torzulások miatt a gyakorlatban ritkán fordul elő.

Ezt a vetületet már az egyiptomiak ismerték. A Kr.e. 2.században Hipparchosz görög csillagász használta csillagtérkép vetületeként. Földi térképekhez először Gemma Frisius németalföldi térképész alkalmazta 1540-ben. A sztereografikus leképezés alapelveit d’Aguillon németalföldi matematikus írta le, az elnevezés is tőle származik.

Szögtartó síkvetület ellipszoid alapfelülettel

A topokartográfiában – például a Gauss-Krüger és az UTM vetületi rendszereknél – a pólus környékének ábrázolására is használják a szögtartó síkvetület normális elhelyezésű változatát, de ellipszoid alapfelülettel. Ennek a B ellipszoidi pólustávolságtól függő sugárfüggvénye az ellipszoid alapfelületre érvényes szögtartási alapegyenletből vezethető le. A parallelkör menti h hossztorzulás:

A meridián menti k hossztorzulás:

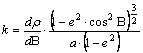
Ezeket egyenlővé téve és a differenciálegyenletet megoldva kapjuk a r sugárfüggvényt:

ahol e az ellipszoid első excentricitása, d pedig az a konstans, amely kijelöli a hossztartó (és így torzulásmentes) parallelkört.

Ha a pólus torzulásmentes, akkor

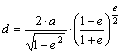
A NATO topokartográfiai világtérképműjénél alkalmazott UTM vetület a Földet csak a D-i szélesség 80°-tól az É-i szélesség 84°-ig ábrázolja; a pólusok környéke viszont a fenti szögtartó síkvetületben készül, a

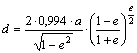
választással. Ez az UPS (Universe Polar Stereographic) elnevezésű vetület (Hayford 1924 alapfelület esetén) a ±81°6’52.2588” szélességen torzulásmentes, a pólusokban 0.994-szeres hossztorzulás lép fel (d=12637636.654785).

Ugyancsak a poláris sztereografikus vetületet használják 1962 óta az 1:1 000 000 geokartográfiai világtérképmű pólus ábrázolásához (az É.sz. 84°-tól az északi, illetve a D.sz. 80°-tól a déli pólusig terjedően). A Hayford 1924 ellipszoid alapfelület választással (d=12621895.458099) a ±80°14’19” szélességi kör torzulásmentes, a pólusban fellépő hossztorzulás: 0.99276189.

Transzverzális és ferdetengelyű sztereografikus síkvetületek

A sztereografikus (érintő) síkvetület transzverzális elhelyezésű változatának vetületi egyenletei megkaphatók a transzverzális perspektív síkvetület vetületi egyenleteiből

c=2 és f=1 helyettesítéssel:

A XVIII. századtól kezdve az atlaszokban előszeretettel ábrázolták a keleti és/vagy a nyugati féltekét ebben a vetületben.

A ferdetengelyű sztereografikus síkvetület egyenleteit hasonlóan kaphatjuk a perspektív síkvetület egyenleteiből c=2 és f=1 mellett (a geodéziai alkalmazás miatt itt kivételesen R sugarú gömbre):

ahol (j₀,l₀) jelöli a vetületi kezdőpont szerepét játszó segédpólus koordinátáit, Dl=l-l₀ pedig a segédpóluson átmenő középmeridiántól mért hosszúságkülönbséget. Lényegében ezt a vetületet használta a magyarországi felsőrendű háromszögelés 1857-től, majd erre tért át az országos felmérés 1863-tól. A felmérés alapfelülete a Bessel-ellipszoid volt; erről a Gauss féle szögtartó gömbvetülettel képeztek le az ún. első magyarországi Gauss-simulógömbre (R=6378512.966m); a második lépésben történt a képsíkra vetítés ferdetengelyű sztereografikus vetülettel. (Ezt nevezték „kettős vetítésnek.”) A koordinátarendszer DNy-i tájolású volt: a D-i irányba mutató tengelyt jelölték x-szel, a Ny-it y-nal. Az akkori országterületen a hossztorzulások csökkentése érdekében két képsíkot vettek fel: az ún.”budapesti rendszer” vetületi kezdőpontját a gellérthegyi háromszögelési pont gömbi képében (j₀=47°6’21.1372”), a Királyhágón túli területek felmérésére szolgáló „marosvásárhelyi rendszerét” a Marosvásárhelytől ÉNy-ra fekvő Kesztej-hegyi pont gömbi képében (j₀= 46° 30’ 22.9804”; l₀= + 5° 20’ 41,8290” a gellérthegyi meridiántól K-re) választották. A katonai térképezés 1927-ben tért át a budapesti sztereografikus rendszer alkalmazására. 1936-tól vezették be az ún. „katonai sztereografikus rendszert”: ennek origóját eltolták a gellérthegyi pontból Ny-ra és D-re 500-500 km-rel, és a koordinátatengelyek irányának felcserélésével a tájolását ÉK-ivé tették.

A ferdetengelyű sztereografikus síkvetület inverz vetületi egyenleteinek meghatározásához induljunk ki a síkkoordináták négyzetösszegéből, ami a sugárfüggvény négyzetét adja meg:

A 4×R²-tel való átosztás után vezessük be az alábbi jelölést:

Ekkor az átszorzás után az egyenlet alakja:

Innen kifejezhető cosj ×cosDl:

Helyettesítsük most a fenti y vetületi egyenletbe a cosj ×cosDl kifejezését:

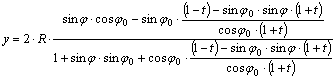
A jobb oldal nevezőjével átszorozva és közös nevezőre hozva:

Elvégezve a kijelölt műveleteket:

Összevonások után kifejezzük sinj-t:

Végül

Hasonlóan helyettesítsük az x vetületi egyenletbe a fenti cosj ×cosDl -t, miután a számlálót cosDl -val bővítettük:

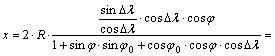
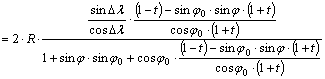
Átszorzás és közös nevezőre hozás után:

A kijelölt műveletek elvégzése és sinj imént kapott képletének behelyettesítése után:

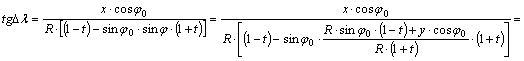
Ebből kapjuk a Dl szöget:

(A magyarországi topokartográfiában használt ferdetengelyű sztereografikus vetületnél ebben a képletben a DNy-i tájolás miatt az y helyére –x, az x helyére –y írandó.)

b) Gnomonikus síkvetület (f=0,c=1)

A vetítés középpontja ebben az esetben egybeesik a gömb középpontjával, a képsík pedig érinti a gömböt (?ábra). A r sugárfüggvény:

Csak félgömbnél kisebb terület ábrázolható, az egyenlítő (b=90°) a végtelenbe távolodik. A fokhálózat menti hossztorzulások:

A hossztorzulásokat a ???ábra szemlélteti. Mivel h¹k és h¹1/k, ezért a gnomonikus vetület általános torzulású. A vetületi kezdőpont torzulásmentes; a pólustól távolodva a hossztorzulási modulusok egyre gyorsabban nőnek, emiatt a szomszédos parallelkörök távolsága rohamosan növekszik. A területtorzulási modulus:

Az w maximális iránytorzulást jellemző mutatószám értékét az alábbi képlet adja:

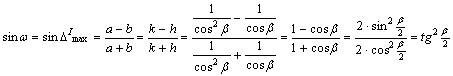
A gnomonikus vetület legfontosabb tulajdonsága, hogy az ortodrómák képe egyenes. A gömbi főkörök síkja ugyanis tartalmazza a gömb középpontját, emiatt a gömbközéppontból kiinduló és az ortodróma pontjain végigfutó vetítősugarak benne maradnak a gömbi főkörív síkjában. Az ortodróma képe tehát e síknak a képsíkkal való metszésvonala lesz, ami egyenes.

A gnomonikus síkvetület transzverzális és ferdetengelyű elhelyezésben is használható, és az ortodrómák képe ezeknél is egyenes lesz. Transzverzális esetben a meridiánok (gömbi főkörök) képei párhuzamos egyenesek lesznek, amelyek az egyenlítő képére merőlegesek; a parallelkörök képei forgáskúpoknak a képsíkkal alkotott metszetei, nevezetesen hiperbolák. Ferdetengelyű esetben a meridiánok (gömbi főkörök) képei a pólus képében összefutó egyenesek, a parallelkörök képei pedig forgáskúpoknak a képsíkkal alkotott metszetei, nevezetesen ellipszisek, hiperbolák illetve egy parabola.

A gnomonikus síkvetületet Thales alkotta meg Kr.e. 580-ban. Alkalmazására akkor kerülhet sor, ha a hátrányos torzulási tulajdonságokra való tekintet nélkül az ortodrómák (pl. útvonalak) egyenesként való megjelenése a cél.

Ortografikus síkvetület (f=¥,c=¥)

A vetítés középpontja a végtelenben van, vagyis a vetítősugarak a képsíkra merőlegesek. (A képsík érintő ill. metsző elhelyezésének emiatt itt nincs jelentősége.) A ???ábrából láthatóan a r sugárfüggvény:

Egyidejűleg egy félgömbnyi terület ábrázolható. A fokhálózat menti hossztorzulások:

A hossztorzulásokat a ???ábra mutatja. Mivel h¹k és h¹1/k, ezért az ortografikus vetület általános torzulású. A vetületi kezdőpont torzulásmentes; a pólustól távolodva a hossztorzulási modulusok a (segéd-) egyenlítőhöz közeledve gyorsan csökkennek, emiatt a szomszédos parallelkörök távolsága is rohamosan csökken. A területtorzulási modulus:

A maximális iránytorzulást (w) jellemző mutatószám értékének kiszámítására szolgáló képlet:

Transzverzális elhelyezésben az ábrázolt féltekén a parallelkörök képei párhuzamos egyenesek, a meridiánok képei ellipszisívek. Ferdetengelyű elhelyezésnél mind a meridiánok, mind a parallelkörök képei ellipszisívek. (Kivételt képez a kezdőmeridián bimeridiánja, amely egyenesként jelenik meg.)

Az ortografikus vetület a Kr. előtti III. században alkotott Apollóniusig vezethető vissza. Elsősorban a Föld távlati képének bemutatására alkalmazzák.

Nem-perspektív valódi síkvetületek

Nem-perspektívek azok a valódi síkvetületek, amelyeket nem lehet előállítani centrális vetítéssel, másként: a sugárfüggvényük nem írható fel a perspektív vetületek sugárfüggvényével megegyező alakban.

A nem-perspektív valódí síkvetületek transzverzális vagy ferdetengelyű elhelyezését a következőképpen értelmezzük. Kijelöljük a segédpólust és egy abból kiinduló, valamely eredeti póluson áthaladó segédmeridiánt.

A vetületi egyenleteket most az így létrehozott b^*,l^* segédföldrajzi koordinátákra vonatkoztatjuk:

A tetszőleges alapfelületi pont b,l koordinátáiból ekkor első lépésben gömbháromszögtani úton kiszámítjuk e pont b^*,l^* segédkoordinátáit, majd ezekből a fenti vetületi egyenletek adják a térképi síkkoordinátákat.

Ha a segédpólus az egyenlítőn van, akkor transzverzális; ha a póluson és az egyenlítőn kívül valahol máshol helyezkedik el, akkor ferdetengelyű síkvetületről beszélünk.

Meridiánban hossztartó valódi síkvetület (Postel féle vetület)

A meridiánok hossztartása valódi síkvetületeknél a

vagyis a

egyenlettel adható meg. Ebből következik, hogy a sugárfüggvény:

ahol a d integrációs konstans a póluspontosság követelménye miatt zérus.

Elméletileg a teljes Föld ábrázolható egy p sugarú körben. (Az egyik pólus a vetületi kezdőpontban van, a másik a kör kerületére képeződik le.) Félgömbnél nagyobb területet azonban a gyorsan növekedő torzulások miatt nem szoktak ábrázolni.

A fokhálózat menti hossztorzulások:

A vetület tehát általános torzulású. A hossztorzulásokat szemléltető ???ábra mutatja, hogy h³k, tehát

és

A vetületi kezdőpont torzulásmentes. k=1 miatt a szomszédos parallelkörök távolsága egyenlő. Emiatt előfordul az „ekvidisztáns (egyenközű) síkvetület” elnevezés is. A területtorzulási modulus:

Az w maximális iránytorzulást jellemző mutatószám értéke:

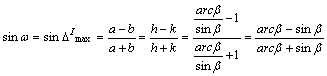
Elsősorban a pólusok környékét ábrázoló térképeknél használják. Más területek ábrázolásánál a központi irányok menti hossztartási tulajdonságát használják ki, nevezetesen: hogy ferdetengelyű változatainál a vetületi kezdőpontba kerülő ponttól egyenlő gömbi távolságra elhelyezkedő pontok a térképen egy kör mentén helyezkednek el. Ezért központi objektumok (híradástechnikai adók, repülőterek, stb.) hatósugarai, vagy valamely településtől való távolságok ábrázolására alkalmazzák. Előfordul csillagtérképek vetületeként is. Transzverzális változata a XVIII. századtól főként atlaszokban fordul elő a féltekék ábrázolásához.

A vetület a nevét egyik alkalmazójáról, Guillaume Postel francia matematikusról kapta (1581), bár előtte a XVI. században a vetületet többen használták, így Mercator is (1569), sőt már az ókori egyiptomiak csillagtérképein is előfordul.

Területtartó síkvetület (Lambert féle síkvetület)

Induljunk ki a területtartás alapegyenletéből:

,

ami esetünkben a r sugárfüggvényére vonatkozólag a

egyenletet jelenti. Ezt rendezzük át és integráljuk:

Elvégezve az integrálást:

A r(0)=0 követelmény miatt d=1. Átalakítva:

Végeredményben kapjuk a r sugárfüggvényt:

E vetületben lehetséges az egész Föld ábrázolása, de a gyorsan növekvő szögtorzulások miatt félgömbnél nagyobb területet ritkán ábrázolnak. A fokhálózat menti hossztorzulások:

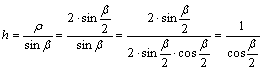
melyeket a ???ábra szemléltet, egyben mutatja, hogy h³k, tehát itt is

és

A szomszédos parallelkörök távolsága a pólustól távolodva fokozatosan csökken.

A területtartással szemben szögtorzulással számolnunk kell, amelynek mértékét az w maximális iránytorzulás adja meg:

Ezt a vetületet a geokartográfiában gyakran használják a pólusok környékének ábrázolására. Ferdetengelyű változata kedvelt bizonyos kontinensek, így Európa, Ázsia, É-Amerika és Ausztrália területtartó megjelenítéséhez. A transzverzális változat a K-i és Ny-i féltekék ábrázolásánál fordul elő, leginkább az atlaszkartográfiában.

A síkvetületek besorolása a Ginzburg féle sémába

Ginzburg orosz kartográfus ajánlott a valódi síkvetületek közelítésére egy általános képletet. Ennek sugárfüggvénye

alakú, ahol L₁, L₂, c₁>0 és c₂>0 konstansok.

a) L₂=0 és L₁= c₁ esetén

.

A meridián menti hossztorzulás:

,

ami a vetületi kezdőpontban egységnyi, onnan távolodva pedig k értéke csökken, ami a parallelkörök távolságának csökkenésében is megmutatkozik.

Ehhez a vetületcsoporthoz tartozik c₁=1 választásnál az ortografikus, c₁=2 esetén pedig a Lambert féle területtartó síkvetület. Ha c₁ 3 és 7 közé esik, akkor a vetület területtorzulása csekély; 1.2 és 1.5 közé eső értékeknél a térképezett terület gömbhöz hasonló megjelenést ad. Ginzburg nyomán használják időnként a c₁=3-hoz tartozó – általános torzulású – síkvetületet.

b) L₁=0 és L₂= c₂ esetén

A meridián menti hossztorzulás:

,

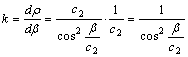ami b=0-nál 1-gyel egyenlő. A pólustól távolodva k értéke növekszik, ami a parallelkörök távolságának növekedését eredményezi.

Ebben a vetületcsoportban találjuk c₂=1 esetén a gnomonikus, c₂=2 esetén pedig a sztereografikus vetületet.

Az a) vetületcsoportnál c₁®¥ esetén, a b) vetületcsoportnál c₂®¥ esetén minden b-ra k®1, vagyis határhelyzetben mindkét vetületcsoport meridiánban hossztartó. Így a Postel féle síkvetület, mint a két vetületcsoport közös határértéke is besorolható ebbe a sémába.