A VETÜLETTAN TÁRGYA

Leképezés az alap- és a képfelület között

A térkép a görbült földfelület tárgyainak, jelenségeinek és folyamatainak alaprajzszerű ill. egyezményes jelszerű ábrázolásából adódó geometriai objektumokat (pontokat, vonalakat vagy felületdarabokat) síkban jeleníti meg, lehetőleg olymódon, hogy a síkbeli méretviszonyok (hosszak, irányok ill. szögek, területek nagysága) a földfelületi méretviszonyoktól kevéssé térjenek el, és így azokra térképi mérések alapján vissza lehessen következtetni. Mind a földfelületi pontok geodéziai helyzetének meghatározásánál, mind az objektumok térképi (tehát síkbeli) ábrázolásánál fontos szerepet játszanak azok a leképezések ("vetületek"), amelyek a görbült földfelületet síkra képezik le. Ezekkel és ezek tulajdonságaival foglalkozik a vetülettan, más néven matematikai kartográfia.

A vetület, mint leképezés tehát egy görbült geometriai felület (az ún. alapfelület) pontjait egy másik geometriai felületre (az ún. képfelületre) képezi le, vagyis az alapfelület minden pontjához a képfelület egy pontját rendeli hozzá. (???ábra) A leképezés matematikai megadásához alapfeltétel, hogy mind az alap-, mind a képfelület lehetőleg folytonos, szabályos, továbbá zárt képlettel leírható legyen. E feltételek sem a topográfiai földfelületre, sem a geoidra (a nehézségi erőtér azon szintfelületére, mely egybeesik a világóceánok közepes szintjével, és képzeletben a kontinensek alatt is folytatódik) nem teljesülnek maradéktalanul. A szabálytalan alakú geoid viszont jól közelíthető egy, a pólusoknál kissé lapult forgási ellipszoiddal, más néven szferoiddal. (Ez egy olyan forgásfelület, amely egy ellipszisnek a kistengelye körüli forgatásából keletkezik.) A csekély lapultság miatt a földi ellipszoid csak kis mértékben különbözik a gömbfelülettől. A vetület alapfelülete ezért (a kívánt pontosságtól függően) forgási ellipszoid vagy gömb. Képfelületként a sík mellett számításba jönnek még az ún. síkba fejthető felületek, amelyek lehetőleg szabályosak, és amelyeket úgy lehet síkká alakítani, hogy eközben a felületen belüli méretviszonyok nem változnak meg (tehát a síkba fejtés során mind a felületi görbék ívhossza, mind az egymást metsző felületi görbék metszéspontbeli érintőinek szöge, mind pedig a felületdarabok felszíne változatlan marad). Ilyen síkba fejthető felület pl. a forgáshenger és a forgáskúp palástja.

Felületek többféle módon is megadhatók zárt képlettel. Mutassuk be ezeket a sík, a gömbfelület és a forgási ellipszoid példáján.

Legelőnyösebb a (Gauss-féle) ún. paraméteres alak, amelyben a felület pontjainak x, y, z térbeli koordinátáit az u,v valós paraméterek folytonos függvényeként adjuk meg:

A v paraméter rögzített értékeinél a felületen a folytonos u-vonalak seregét, az u paraméter rögzített értékeinél a folytonos v-vonalak seregét kapjuk, amelyek a felületet egyrétűen fedik le (??? ábra). A felület minden pontján áthalad egy u- és egy vele nem párhuzamos v-vonal. Sem az u-vonalak, sem a v-vonalak nem metszhetik egymást.

Például a sík paraméteres alakja:

Az R sugarú, origó-centrikus gömb is megadható paraméteres alakban (ennek részleteit ld. a következő fejezetben):

Ebből z irányú, P/R arányú merőleges affinitással előáll a forgási ellipszoid egyik lehetséges paraméteres alakja:

A felületeket másrészt meg lehet adni

egyenlet alakjában is, ami egy skalár-vektor függvény szintfelületét jelenti, és gyakran egyszerűbb a paraméteres alaknál. A sík egyenlete pl.:

Az r sugarú, origó-centrikus gömb egyenlete:

Az r nagy-féltengelyű, p kis-féltengelyű, origó-centrikus és z forgástengelyű forgási ellipszoid egyenlete:

A felületek x, y, z koordinátájú pontjainak egy további megadási módja a kétváltozós

(Euler-Monge féle) függvény-alak, amely az egyenlet-alak speciális esetének tekinthető. Hátránya, hogy egyes felületek csak többértékű függvénnyel írhatók le. A síkot ebben az esetben a

,

a gömbfelületet a

,

a forgási ellipszoid felületet pedig a

függvény adja meg.

A vetülettan tehát elsősorban a geodéziában és a térképészetben előforduló földi vetületekkel foglalkozik, melyek a gömböt vagy forgási ellipszoidot síkra vagy síkba fejthető felületre képezik le. (Kivételt képeznek az ún. gömbvetületek, amelyek a forgási ellipszoid felületének pontjaihoz gömbfelületi pontokat rendelnek hozzá.)

A vetületek megadása

A vetületek elnevezése (más nyelveken is) azt sugallja, mintha a vetületeknek közvetlen köze volna a centrális vetítésnek nevezett geometriai transzformációhoz. Valójában a korszerű vetület-fogalom egy felület pontjainak egy másik felület pontjaira történő matematikai leképezésén alapul. A vetületek között azonban speciális helyet foglalnak el az ún. "perspektív vetületekek", amelyeket az alap- és képfelület megfelelő elhelyezése útján centrális geometriai vetítéssel elő lehet állítani (???ábra). Ezek fontos szerepet játszottak a vetülettan elméletének kifejlődésében, és közülük néhány ma is használatban van. A perspektív vetületek képfelülete egyaránt lehet sík, forgáshenger-palást vagy forgáskúp-palást. A vetületek többségét képező nem-perspektív vetületek képfelülete viszont kizárólag sík.

A vetületeket úgy kell megadni, hogy az alapfelület pontjairól a képfelület pontjaira történő leképezés illetve átszámítás minden ábrázolandó pontra nézve lehetséges és egyértelmű legyen. Ez perspektív vetületek esetén geometriailag is megvalósítható volna, de a nem-perspektív vetületekre tekintettel más megoldást kell választani, ami a "vetületi egyenleteknek" nevezett leképezési függvények alkalmazásával válik lehetővé. Ezek a térképi síkkoordinátákat a (következő fejezetben értelmezendő) földrajzi szélesség és hosszúság függvényében adják meg:

és

A vetületi egyenletekkel szemben az alábbi követelményeket támasztjuk:

1. Létesítsenek kölcsönösen egyértelmű (injektív) megfeleltetést az ábrázolandó területre vonatkozólag az alap- és a képfelület pontjai között.

2. Lehetőleg egyetlen zárt matematikai képlettel vagy sorral leírhatók legyenek.

3. Legyenek az ábrázolandó terület minden pontjában kétszer folytonosan differenciálhatók.

Ezeknek a követelményeknek a gyakorlati térképkészítés vetületei nem tesznek mindig tökéletesen eleget.

- A kölcsönös egyértelműség pl. nem teljesül a világtérképek két határoló meridiánképére, amelyek az alapfelület egyetlen meridiánjának felelnek meg. A pólus képe gyakran egy vonal, ilyenkor egyetlen alapfelületi pontnak végtelen sok képfelületi pont felel meg.

- Vannak olyan vetületek, amelyeknek nincsenek egységes vetületi egyenletei, hanem bizonyos szélességi körök által elhatárolt övezetenként más és más vetületi egyenlet érvényes.

- E vetületek között vannak olyanok, ahol a vetületi egyenletek mint függvények az elhatároló fokhálózati vonalakon nem tesznek eleget a differenciálhatósági feltételeknek, emiatt a térképen fellépő vetületi torzulások e vonalon ugrásszerűen változhatnak.

Bizonyos esetekben a vetületi egyenletek inverzei is felírhatók explicit alakban, ekkor a

és

függvények segítségével valamely térképi pont síkkoordinátáiból az alapfelületi őskép földrajzi koordinátáit tudjuk kiszámítani.

A vetületi torzulásokról általában

A görbült földet modellező szabályos alapfelületről a síkra, vagy síkba fejthető más képfelületre történő leképezés során az alapfelületi objektumok bizonyos méretviszonyai megváltozhatnak, ezeket a változásokat vetületi torzulásoknak nevezzük. Lássuk be először, hogy bizonyos hosszak minden vetületben torzulnak.

Egy adott felület görbeívei közül azt nevezzük geodéziai vonalnak vagy ortodrómának, amely a két végpontot összekötő felületi görbeívek közül a legrövidebb. Sík esetén a geodéziai vonal a két végpontot összekötő egyenes szakasz, gömbfelület esetén pedig a két végponton áthaladó gömbi főkör ívek közül a rövidebbik. (Bonyolultabb a helyzet a forgási ellipszoid felületénél, mert ott a geodéziai vonal általában nem síkgörbe.)

Tételezzük fel most, hogy létezik olyan "hossztartó" vetület, amelynél a gömbnek választott alapfelületi ívek hosszai mindig megegyeznek ezek képfelületi megfelelőinek ívhosszával. Ha volna ilyen leképezés, annál az alapfelület geodéziai vonalainak képe szükségszerűen a képfelület geodéziai vonala kellene legyen. Földi vetület esetén tehát a gömb-alapfelületi ortodróma-íveknek egyenes szakaszokra kellene leképeződniük.

Tekintsünk most a gömb alapfelületen egy olyan gömbháromszöget, amelynek egyik csúcsa a pólusban, a másik két csúcsa az Egyenlítőn helyezkedik el egymástól 90°-nyira. Ennek a (szabályos) gömbháromszögnek mindhárom oldala és szöge 90°-os. A fentiek szerint a feltételezett "hossztartó" vetületünknek ezt egy olyan szabályos síkháromszögre kellene leképeznie, amelynek oldalhossza megegyezik a gömbháromszög oldalhosszával. Vegyünk most egy olyan ortodróma-ívet, amely a pólustól a gömbháromszög szemközti oldalának egy belső pontjához vezet (??? ábra). Ennek alapfelületi hossza megegyezik a gömbháromszög oldalhosszával (90°), azonban a képfelületen egy olyan egyenes szakaszra képeződik le, amely a síkháromszögekre vonatkozó ismert tétel miatt a háromszögünk oldalánál kisebb. Ez ellentmond a kezdeti "hossztartósági" feltételünknek, következésképpen kimondhatjuk, hogy "hossztartó" vetület nincs. (Hasonló gondolatmenet forgási ellipszoid alapfelület esetén is érvényes.) A szükségszerűen fellépő hossztorzulások mellett a térképen az irányok ill. a szögek, valamint a területek is torzulhatnak.

A vetületek legfontosabb tulajdonságai a torzulási viszonyaikra vonatkoznak. Egy vetület alkalmazása előtt tudnunk kell, hogy milyen alapfelületi objektumok torzulnak és milyen mértékben, hol helyezkednek el a torzulásmentes helyek. A vetület torzulási tulajdonságai és a térkép bármely pontjában fellépő torzulási viszonyok a vetületi egyenletekből levezethetők.

A térkép méretaránya

A mindennapi életben a műszaki tervekre, helyszínrajzokra, stb. használt méretarány-fogalom a rajzi távolságnak és a megfelelő valódi távolságnak a hányadosa. Ettől eltér a térképi méretarány fogalma. Ehhez gondoljuk végig a térképkészítés elvi folyamatát.

Első lépésben a görbült földfelületet vagy egy részét síkra képezzük le. A leképezés egy földi méretű képzeletbeli síkra történik, amelyen aztán a gyakorlati használhatóság céljából egy arányos kicsinyítést hajtunk végre; ez eredményezi a kézben tartható térképet (??? ábra). A térkép tehát egy vetület és egy hasonlósági transzformáció egymás utáni alkalmazásából keletkezik. Ennek a hasonlósági transzformációnak az arányát nevezzük a térkép (névleges v. elméleti) méretarányának. Vagyis képletben:

A térkép méretaránya tehát egyetlen, az adott térképre jellemző szám (arány). Viszont a térképi hossznak a megfelelő alapfelületi valódi hosszhoz való aránya - ahogyan a köztudatban a méretarány fogalma él - a vetületi torzulások miatt attól függ, hogy a vizsgált vonal, amelynek a hosszáról itt szó van, a térkép melyik részén helyezkedik el. Ha van a térképünknek hossztartó vonala, akkor az e mentén vett ívek térképi és valódi hosszának aránya megegyezik a térkép névleges méretarányával. A torzulásmentes vonalat izodeformációs vonalnak hívjuk. Izodeformációs övnek azon térképi pontok összességét nevezzük, ahol a névleges méretarány a térkép és a valóság közötti hossz-átszámításhoz gyakorlati szempontból használható. Ennek kiterjedése egy adott vetület esetén természetesen függ az elvárt pontosságtól: ennek növelésével az izodeformációs öv keskenyebbé válik.

A térkép vetületének grafikus előállítása

A vetületi egyenletek és a névleges méretarány ismeretében az ábrázolandó területnek adott vetületben való megjelenítésére több gyakorlati módszer szolgál:

- Az ismert koordinátájú, ábrázolandó alapfelületi pontok koordinátáit a vetületi egyenletek és a méretarány segítségével képfelületi koordinátákká alakítjuk át, és ez alapján a pontot a képsíkon elhelyezzük: ez az ún. koordináta-módszer. Ezen az elven dolgoznak a számítógépes megjelenítő eszközök: a képernyő, a rajzgép, a nyomtató.

- Az alapfelületi pontokat összekötő geodéziai vonalak hosszát a hossztorzulási arány segítségével képfelületi távolságra számítjuk át, az alapfelületi szögeket pedig az irányredukciókkal korrigáljuk. Az így kapott távolságok és szögek segítségével és a méretarány figyelembevételével a pontokat a képsíkra rajzeszközzel felvisszük. Ezt nevezzük redukciós módszernek.

- A görbeseregek módszerénél az alapfelületen felveszünk két, egymást metsző görbesereget (többnyire valamilyen kerek fokértékű hosszúsági és szélességi köröket), majd a képfelületen – koordináta-módszer, esetleg a redukciós módszer segítségével –megjelenítjük legalábbis ezek metszéspontjait, de lehetőség szerint e fokhálózati vonalak képeit. Végül interpolációval határozzuk meg a köztük lévő ábrázolandó pontok helyét. Az újonnan szerkesztett kis méretarányú térképek többnyire így készülnek.

ALAPFOGALMAK AZ ALAP- ÉS KÉPFELÜLETEN

Az alapfelület paraméterezése

Állítsuk elő alkalmas paraméteres alakban az alapfelületként használt geometriai felületeket: tehát a gömböt és a forgási ellipszoidot.

Gömb alapfelület esetén a paraméterezés a gömbközéppontban felvett origójú térbeli polárkoordináta-rendszeren alapul, melynek polártengelye kijelöli az (É-i) pólust (???ábra). Vegyünk fel egy tetszőleges P pontot a gömb felületén. Az origótól a P-hez vezető rádiuszvektornak (egyúttal a gömbfelület normálisának) – a polártengellyel bezárt b szöge (a pólustávolság), illetve ennek pótszöge, a j(=90°-b) földrajzi szélesség adja az egyik paramétert. A koordinátarendszer kezdő-félsíkja (melynek határa a polártengelyre esik) a gömbfelületen kijelöli a kezdőmeridiánt. Most az alapfelületi P pontot tartalmazó, a polártengely által határolt félsíknak a kezdő-félsíkkal bezárt szöge adja a másik paramétert, a l földrajzi hosszúságot. (A harmadik polárkoordináta, a rádiuszvektor r hossza , amely megegyezik a gömb sugarával, minden P pontra azonos, így ez a P pont megadásánál figyelmen kívül hagyható.)

(A kezdőmeridiánnal nem keverendő össze a középmeridián, amely az ábrázolt terület középvonalában haladó, többnyire kerek értékű hosszúsági kör. Ez általában a fokhálózat képének szimmetriatengelye, így a képfelületen egyenesként jelenik meg, és rendszerint kijelöli az egyik koordinátatengelyt vagy annak irányát.)

A paramétervonalakat a j ill. l paraméterek rögzítésével kapjuk. Az azonos j földrajzi szélességű (egyben azonos pólustávolságú) pontok által meghatározott gömbi körök a szélességi körök vagy parallelkörök. (Ezek között kitüntetett szerepet játszik a 0°-os szélességi kör, az egyenlítő.) Az R sugarú gömbön a j szélességi kör r sugara:

,

az egyenlítő sugara így R. A földrajzi szélességet előjellel is ellátjuk, amelyet az É-i félgömbön tekintünk pozitívnak (vagyis –90°£j£90°, és 0°£b£180°). A l földrajzi hosszúságot a K-i féltekén tekintjük pozitívnak (vagyis -180°£l£180°). Az azonos földrajzi hosszúságú pontok által meghatározott gömbi főkörívek (félkörök) a hosszúsági körök vagy meridiánok. A hosszúsági kör sugara mindig R.

A gömb paraméteres alakja az előző fejezetben megadott módon az u=j és v=l helyettesítéssel adódik:

Forgási ellipszoid alapfelület esetén ugyancsak térbeli polárkoordinátarendszerből indulunk ki, melynek origója az ellipszoid centrumával, polártengelye az ellipszoidfelület forgástengelyével esik egybe. A pólustávolságnak megfelelő B paramétert most az ellipszoidfelület P pontbeli normálisának a polártengellyel bezárt szöge adja meg, ennek pótszöge a F(=90°-B) (ellipszoidi) földrajzi szélesség, amelyet a gömbnél elmondott módon előjelezünk (???ábra). A L (ellipszoidi) földrajzi hosszúságot a gömbhöz hasonlóan, a P pontot tartalmazó félsíknak a kezdő félsíkkal alkotott (előjeles) szöge segítségével definiáljuk.

A F paramétervonalak, vagyis az azonos földrajzi szélességű illetve azonos pólustávolságú pontok itt is egy szélességi kör vagy parallelkör mentén helyezkednek el, melyek az ellipszoidfelület forgástengelyre merőleges körmetszeteként is előállíthatók. Jelöljük a-val illetve b-vel a forgási ellipszoid nagyobb illetve kisebb féltengelyét. A szélességi kör r sugarát és síkjának az egyenlítő síkjától mért z távolságát az alábbi képletek adják meg:

és

(Az egyenlítő sugara tehát a.) A L paramétervonalak, vagyis az azonos földrajzi hosszúságú pontok most egy fél-ellipszis alakú meridiánt határoznak meg, melynek az egyenlítő síkjában fekvő nagy féltengelye a, a forgástengelyen lévő kis féltengelye b (???ábra).

Ezekkel a paraméterekkel – bevezetve az és az jelöléseket –

– a forgási ellipszoid az alábbi módon írható fel:

A F ellipszoidi szélességet geodéziai szélességnek is hívjuk. Ez különbözik az ellipszoid középpontjától a P ponthoz vezető rádiuszvektornak az ellipszoidi egyenlítő síkjával bezárt szögétől, amelyet (Y-vel jelölve) geocentrikus szélességnek nevezünk (???ábra). (Az ellipszoidon a geodéziai szélesség a geocentrikus szélességgel csak a pólusban és az egyenlítőn egyezik meg; gömb alapfelület esetén ez a két szélesség mindenütt azonos, mivel a P ponthoz vezető rádiuszvektor egyben merőleges a gömb felületére.) Tekintsük most azt a gömböt, amelynek középpontja a földi ellipszoid centruma, sugara pedig annak fél nagytengelye. Ekkor az ellipszoidi pontnak a forgástengellyel párhuzamos gömbfelületi vetületéhez vezető rádiuszvektor egyenlítősíkkal bezárt szöge a (z-val jelölt) ún. redukált szélesség, mely a pólusban és az egyenlítőn szintén egybeesik a geodéziai szélességgel.

A forgási ellipszoid paraméteres alakja az előző fejezetben megadott módon az u=z és v=L helyettesítéssel adódik:

Felmerül a kérdés, hogy milyen kapcsolat van a forgási ellipszoid paraméterei és a geoidon mérhető koordináták között. A geoidon elhelyezkedő P pont koordinátáit meghatározhatjuk pl. csillagászati módszerekkel: a pont pólustávolságának a helyi függőleges és a sarkcsillag iránya által bezárt szöget tekintjük; e szög pótszöge az ún. csillagászati (asztronómiai) szélesség (???ábra); a hosszúság pedig a pontbeli és a Greenwich-i delelés időpontjának különbségéből számítható. A geoidfelület normálisa (a nehézségi erő irányát megadó függővonal) és a geoidhoz illesztett forgási ellipszoid mint elméleti referenciafelület normálisa kis mértékben különbözhet egymástól, ez az ún. függővonal-elhajlás, ami előidézi az asztronómiai és a geodéziai szélesség eltérését.

Ha gömb- és ellipszoidfelületi pontokat, mint térbeli objektum pontjait a fentiek szerint x,y,z derékszögű koordinátákkal adjuk meg, akkor a koordinátarendszer origója értelemszerűen a gömb illetve ellipszoid középpontjába kerül. A z tengely a polártengellyel esik egybe, az x tengelyt pedig rendszerint a kezdőfélsík iránya jelöli ki. Az xy sík ekkor az egyenlítő síkjára esik. Az ellipszoidfelületi pontok derékszögű koordinátáit a műholdas helymeghatározás használja.

A (gömbi vagy ellipszoidi) hosszúság méréséhez szükség van a kezdőfélsík, vagyis a kezdőmeridián kijelölésére. A geokartográfiában és a topográfiai térképműveknél manapság általában Greenwich-i kezdőmeridiánt használják. Régebben - főleg Európában - elterjedt volt a Ferro-i (ma Hierro, Kanári-szigetek) kezdőmeridián használata, amely Greenwich-től mintegy 17°40'-re Ny-ra fekszik. K-Európa több országában Pulkovo-i kezdőmeridiánnal dolgoztak, amely Greenwich-től mintegy 30°20'-re K-re helyezkedik el. A magyarországi térképezéseknél a gellérthegyi meridián játszik fontos szerepet, amelynek a ferroi kezdőmeridiántól való eltérését a Bessel-ellipszoidon 36°42'51.69"-nek tekintették, míg a greenwichi hosszúsága az IUGG'67-es ellipszoidon 19°2'54.856"-nek van megállapítva.

Az alapfelület paraméterezése lehetséges egy, a felületen értelmezett polárkoordinátarendszer segítségével is. Vegyük fel ehhez az O origót valahol a pólustól különböző pontban, valamint egy kezdőirányt, amely rendszerint a pólus felé mutat és így egy meridián irányával esik egybe. A tetszőleges alapfelületi P ponthoz tartozó polártávolságot az OP ortodrómaív hossza adja, míg a polárszög - az ún. azimut - az OP iránynak a kezdőiránnyal bezárt szöge, az óramutató járásával megegyező irányban mérve, melyet 0° és 360° közé esőnek tekintünk (???ábra). A polárkoordinátákkal adott P pont földrajzi koordinátáinak kiszámítását első geodéziai alapfeladatnak nevezzük. Ha a földrajzi koordinátákkal adott P pont polárkoordinátáit számítjuk ki, akkor a második geodéziai alapfeladatot oldjuk meg. Gömb alapfelület esetén mind az első, mind a második geodéziai alapfeladat gömbháromszögtani összefüggésekkel oldható meg.

Gömb alapfelület esetén értelmezhető a segédföldrajzi koordinátarendszer. Ehhez először is ki kell jelölni a gömbön a segédpólust és ezzel együtt a segédpoláris tengelyt. A segédpólustól egyenlő gömbi távolságra (segédpólustávolságra) lévő pontok képezik a segédparallelköröket, 90°-os gömbi távolság esetén a segédegyenlítőt. A segédpólustávolság pótszöge a j* segédszélesség. A két segédpólust összekötő gömbi főkörívek a segédmeridiánok. Ezek közül egyet segédkezdőmeridiánnak választva, ennek félsíkja bármely segédmeridián félsíkjával a segédhosszúságnak nevezett l* szöget zárja be. A segédhosszúságot a segéd-É-i pólus felől nézve az óramutató járásával ellentétesen irányítjuk, és nagyságára: -180°£l*£180°. (Megjegyezzük, hogy az esetek túlnyomó többségében a segédkezdőmeridián tartalmazza az egyik pólust, ugyanis a pólusokon és a segédpólusokon áthaladó gömbi főkör - bimeridián - egy-egy szakasza meridián és egyben segédmeridián is.) A segédföldrajzi koordinátarendszer bevezetésének fő előnye abban áll, hogy segítségükkel bizonyos rokonvetületek egységesen tárgyalhatók, és ezek vetületi egyenletei egyszerű, egységes alakban adhatók meg.

Tetszőleges gömbfelületi (j,l) koordinátákkal megadott pont segédföldrajzi (j*,l*) koordinátáinak meghatározása a második geodéziai alapfeladatra vezethető vissza, míg a segédföldrajzi (j*,l*) koordináták ismeretében az első geodéziai alapfeladat megoldása alapján kapjuk a (j,l) földrajzi koordinátákat, mindkét esetben gömbháromszögtani összefüggések segítségével.

A képfelület paraméterezése

A képfelületet (az esetleges síkbafejtés után) paraméterezhetjük síkbeli derékszögű x,y koordinátarendszer segítségével. Az egyik koordinátatengelynek célszerűen a fokhálózat szimmetriatengelyét vagy egy azzal párhuzamos egyenest választjuk. Ennek irányát szokás hálózati északi iránynak is nevezni. A geodéziában előszeretettel tekintik a hálózati északi irányt x-nek, szemben a matematikában és a vetülettanban inkább szokásos y-nal.

A vetületek egy részénél, különösen kúppalást-képfelületnél, de általában körív alakú parallelkör-képek esetén előnyös a polárkoordinátarendszer bevezetése. A koordinátarendszer origója a körív középpontjába kerül, a polártengely többnyire a középmeridiánnal esik egybe. (Nem-koncentrikus körívek esetében az origó helyzete így a szélesség függvényében akár változhat is.)

A képfelületi síkkoordinátarendszer origóját szokás vetületi kezdőpontnak nevezni.

Nevezetes alapfelületi vonalak és felület-darabok

Most áttekintjük az alapfelületen előforduló nevezetes vonalfajtákat, a paramétervonalakat is beleértve. A vetülettanban az alapfelületi vonalak három fajtája: az ortodróma, a gömbi (ellipszoidi) körív és a loxodróma játszik központi szerepet.

Az ortodróma – mint már említettük – a geodéziai vonal szokásos elnevezése. Gömb alapfelület esetén tehát minden 180°-nál nem nagyobb középponti szöghöz tartozó főkörív ortodróma, így a (segéd-)meridiánok és a (segéd-)egyenlítő is. A meridiánokkal és az egyenlítővel egybe nem eső gömbi főköröket szokás harántköröknek is nevezni. Az ortodróma ívhosszát gömbön a radiánban megadott középponti szögnek az R sugárral való szorzata adja. A Dj szélességkülönséghez tartozó meridiánív mint speciális ortodróma s hossza így:

A forgásfelületek (így a gömb- és a forgási ellipszoid-felületek) ortodrómáinak fontos tulajdonságát fogalmazza meg a Clairaut-tétel. Eszerint a forgásfelület parallelköre és a geodéziai vonal által bezárt szög koszinuszának és a parallelkör sugarának a szorzata – a geodéziai vonal mentén haladva – nem változik. A minden parallelkört merőlegesen metsző felületi görbék – a meridiánok – esetén ez a szorzat zérus, emiatt a meridiánok geodéziai vonalak. Tetszőleges felületi görbe meridiánnal bezárt szögét azimutnak nevezzük. Jelölje a az azimutot, és r a geodéziai vonal pontjának a forgástengelytől mért távolságát (másként a ponton áthaladó parallelkör sugarát); ekkor Clairaut tétele képletben az alábbi alakot ölti:

A fentiek miatt a forgási ellipszoid alapfelület speciális ortodrómái a meridiánok (ellipszisek), míg az összes többi ortodróma térgörbe. A F₁ és F₂ szélességek közötti meridiánívhosszat az ellipszisív simulókör-sugarának (az M-mel jelölt ún meridiángörbületi sugárnak) a földrajzi szélesség szerinti integráljaként kapjuk:

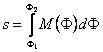, ahol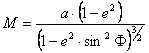

A parallelkörök mind gömbön, mind forgási ellipszoidon a poláris tengelyre nézve forgásszimmetrikus körök, amelyek gömb alapfelület esetén (az egyelítőt kivéve) gömbi kiskörök. E j szélességű parallelkörön egy Dl hosszúságkülönbséghez tartozó ív s hossza:

.

A gömbfelületen a parallelkörökön kívül további felületi kiskörök is felvehetők. Egy ilyen kiskörön az ívhosszat – alkalmasan felvett segédföldrajzi koordinátarendszerben – az

képlet adja.

Forgási ellipszoid alapfelület F szélességű parallelkörén a DL hosszúságkülönbséghez tartozó s ívhossz a parallelkör

képlettel megadott sugarának a DL hosszúságkülönbséggel való beszorzásából adódik, vagyis:

Az egyenlítő, mint speciális a sugarú parallelkör mentén ez

-vá egyszerűsödik.

A F szélességű parallelkör síkjának az egyenlítő síkjától mért z távolsága:

Loxodrómának azokat az alapfelületi vonalakat nevezzük, amelyeknek minden pontjában az a azimut állandó. A meridiánok az a=0° és a=180° azimuthoz tartozó speciális loxodrómák, a parallelkörök pedig az a=90° és a=270° azimuthoz tartozó speciális loxodrómák. A többi loxodróma olyan csavarvonal, amely az egyik pólusból a másik pólusba vezet. Írjuk fel gömb alapfelületre egy ilyen loxodróma egyenletét az egyértékűség miatt l=l(j) alakban. Ehhez változtassuk meg a j,l koordinátájú pontot Dj,Dl-val, ami egy kis foktrapézt hoz létre a gömbön, melynek oldalai arcDj és arcDl×cosj ; átellenes csúcsait kössük össze egy Ds hosszúságú loxodróma-ívvel (???ábra). A kicsiny foktrapéz oldalai és "átlója" közelítőleg síkban lévőnek tekinthetők, amelyben

; ezt egyszerűsítve és átrendezve:

Ha most a loxodrómát kis darabokra bontjuk, akkor az összegzés, majd a minden határon túli finomítás után az integrálás az alábbi eredményre vezet:

;

innen

A C integrációs konstans megadható, ha a loxodróma pl. a j₀ ,l₀ koordinátájú ponton halad át, ekkor az egyenlet az alábbi alakú:

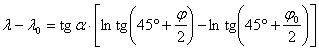
Egyenletünk szerint minden j-hez egyetlen l tartozik, és j®±90° esetén l®±¥. Egy l-hoz viszont (a¹90° esetén) végtelen sok j is tartozhat.

A j₁,l₁ és j₂,l₂ koordinátájú pontokon áthaladó loxodróma azimutja:

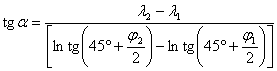
Az a azimuthoz tartozó loxodróma j₁ és j₂ szélességek közé eső darabjának ívhossza szintén az iménti ábra alapján adható meg, ugyanis:

, ahonnan

A loxodróma-ívet kis részekre felosztva, a képletet az egyes részekre alkalmazva összegzünk, ami a minden határon túli finomítás után integrálásba megy át:

innen ,

vagyis a loxodróma-ív hossza az íven fellépő szélességmegváltozás lineáris függvénye.

Említsünk meg néhány, alapfelületi vonalak által határolt nevezetes felületdarabot.

A térgeometriából ismert, hogy egy gömbfelületet egy sík két gömbsüvegre bont fel. Két párhuzamos síkkal elmetszve a gömbfelületet, a két gömbsüveg között egy gömbövet kapunk. A j₁ és j₂ (j₁£j₂) szélességek közé eső gömböv F felszíne:

(j₁ =-90° vagy j₂ =+90° esetén ugyanez a képlet megadja az egy parallelkör által határolt gömbsüveg felszínét.)

A forgási ellipszoidon az egyenlítő (F₀ =0°) és F szélességi kör közé eső ellipszoid-öv F felszíne:

Ugyanez sor alakjában felírva:

A F -be 90°-ot helyettesítve kapjuk a fél-ellipszoid felszínét, ennek kétszereséből pedig az F_e ellipszoidi felszínt:

A fentiek alapján a F₁ és F₂ szélességi körök közé eső ellipszoid-öv F felszíne:

illetve ugyanez sor-alakban:

Kössük össze a gömbfelület egyik átmérőjének végpontjait két gömbi főkörívvel (félkörrel); ezek a gömbfelületet két gömbkétszögre bontják. A l₁ és l₂ meridián által közrezárt gömbkétszög a teljes gömbfelszín (4×R²×p) arányos része, F felszíne tehát:

A forgási ellipszoidon is kijelölhető a határoló L₁ és L₂ meridiánokkal egy ellipszoidi kétszög (zóna); ennek F felszíne a forgási ellipszoid teljes felszínének arányos része:

A térképészetben jelentős szerepet játszik a j₁ és j₂ (j₁£j₂) parallelkör, valamint a l₁ és l₂ (l₁£l₂) meridián által határolt felületdarab, az ún. foktrapéz. Ennek F felszíne gömb alapfelületen:

Forgási ellipszoid alapfelületen a F₁ és F₂ (F₁£F₂) parallelkör, valamint a L₁ és L₂ (L₁£L₂) meridián által határolt foktrapéz felszíne:

A gömb alapfelületen végzett számítások fontos eszköze a gömbháromszög, amelyet három gömbi főkörív határol. A gömbháromszögnek három oldala és három szöge van, amelyek közül általános esetben három mennyiség független, a többi a gömbháromszögtani tételek segítségével kiszámolható. Ha a gömbháromszög szögeit a, b és g jelöli, akkor a gömbháromszög F felszíne:

.

A gömháromszög felszíne negatív nem lehet, így a+b+g ³180°. Az e=a+b+g –180° mennyiséget gömbi szögfölöslegnek nevezzük. Ennek felhasználásával:

.

Másrészt a konvex gömbháromszög szögeinek összege 540°-nál kisebb.

A térképészeti számításokban gyakran használnak olyan gömbháromszögeket, amelyeknek egyik csúcsa a pólusban van. Az ilyen gömbháromszögeket szokás polárgömbháromszögnek nevezni.

A síkháromszögek sok tulajdonsága a gömbháromszögekre is átvihető. Így pl. két oldal összege nagyobb a harmadik oldalnál. A gömbháromszögben nagyobb oldallal szemben nagyobb szög, egyenlő oldalakkal szemben egyenlő szög helyezkedik el. Ezek alapján az általános gömbháromszögek mellett beszélhetünk az egyenlő szárú (szimmetrikus) és az egyenlő oldalú (szabályos) gömbháromszögekről.

A gömbháromszögekre vonatkozó tulajdonságok egy részénél előnyös, ha egységsugarú gömbön vizsgáljuk ezeket. Ekkor a gömbháromszög oldalai megadhatók a hozzájuk tartozó középponti szögekkel. A továbbiakban tehát a gömbháromszög oldalait is szögekkel adjuk meg. Az általános gömbháromszögek oldalai és szögei közül három tetszőleges adat független, a többi adat az alábbi összefüggésekkel határozható meg.

A gömbháromszög szögeire és a velük szemközti oldalak arányaira vonatkozik az ún. gömbháromszögtani szinusztétel:

A gömbháromszög oldalai és egyik szöge között teremti meg a kapcsolatot az ún. gömbháromszögtani oldal-koszinusztétel, pl. az a szögre és a vele szemközti a oldalra felírva:

A gömbháromszög szögei és egyik oldala közötti összefüggést az ún. gömbháromszögtani szög-koszinusztétel adja meg, pl. az a oldalra és a vele szemközti a szögre felírva:

Ha adott a három oldal, vagy két oldal és a közbezárt szög, akkor az oldal-koszinusztétellel; ha a három szög, vagy egy oldal és a rajta fekvő két szög, akkor a szög-koszinusztétellel lehet elindulni a megoldásban.

A fenti tételek kombinálásával minden ismeretlen adat kiszámítható, de gyakran jól hasznosítható az ún. második alapforma is, amely két oldal, a közbezárt szög és valamelyik másik szög között létesít összefüggést:

(A baloldalon szereplő oldalak kiválasztása és sorrendje szerint összesen 6 alakja írható fel.) Mint látható, az a oldal és az a szög ebből kifejezhető, azonban a b oldal és a g szög kiszámítása másodfokú egyenletre vezet.

A polárgömbháromszögekhez kapcsolódik egy további fogalom, a meridiánkonvergencia. A meridiánok a pólus felé összetartanak, ennek mértékét fejezi ki a valódi alapfelületi meridiánkonvergencia. Vegyünk két pontot (P₁ és P₂) az alapfelületen, aztán kössük össze ezeket egymással és a pólussal ortodrómaívek segítségével. A két pontbeli azimut különbségének 180° feletti része a g-val jelölt valódi alapfelületi meridiánkonvergencia. Képletben:

Gömb alapfelület esetén a P₁, a P₂ és pólus által meghatározott polárgömbháromszög szögeire (???ábra) teljesül, hogy

ahol Dl a két pont hosszúságkülönbsége és e a gömbi szögfölösleg. Átrendezve az egyenletet:

Innen kapjuk a g valódi gömbi meridiánkonvergencia és az e gömbi szögfölösleg közötti összefüggést:

.

A vetületi meridiánkonvergencia az a m -vel jelölt szög (???ábra), amelyet a képfelületi P' ponton áthaladó meridiánkép érintője a képfelületi derékszögű koordinátarendszer hálózati északi irányt kijelölő tengelyével bezár, és amelyet az óramutató járásával ellentétesen irányítunk. A vetületi meridiánkonvergenciának a vetületek geodéziai alkalmazásánál van szerepe.

A VETÜLETI TORZULÁSOK

A bevezetőben láttuk, hogy a térképen a hosszak torzulásával mindenképpen számolnunk kell. A térképhasználat során a hosszak mérésén kívül szükség lehet a szögek és a területek mérésére is. A térképi mérésekből csak a torzulások mértéke és eloszlása ismeretében tudunk megbízhatóan következtetni az alapfelületi mértékekre, ezért a torzulások meghatározása a vetülettanban központi szerepet játszik. Ehhez először pontosan definiálnunk kell a vetületi torzulások fogalmát.

A torzulási arányok

Torzulási arány alatt a véges nagyságú objektumok térképi és alapfelületi méretének arányát értjük. A hossztorzulási arány definiálásához vegyük egy mérhető hosszúságú alapfelületi vonal ívhosszát (s) és pontonként vetített képfelületi megfelelőjének s' ívhosszát. (A vetületi egyenletek tulajdonságaiból adódóan s' általában létezik.) Ekkor az l hossztorzulási arány:

A szögtorzulási arányhoz tekintsünk két, egymást metsző sima (törésmentes) görbét, és ezeknek képfelületi megfelelőit, amelyek a vetületi egyenletek tulajdonságaiból következőleg szintén egymást metszők és simák lesznek. Az egymást metsző vonalak által bezárt szög alatt a metszéspontbeli érintőik által bezárt szöget értjük. Legyen az érintők szöge az alapfelületen d, a képfelületen d'. Ekkor az i szögtorzulási arány:

Első irányredukciónak nevezzük az érintők alapfelületi és képfelületi szögének D=d-d' különbségét.

A második irányredukció fogalmához szükség van a vizsgált O pontban egy kezdőirány megadására mind az alap-, mind pedig a képfelületen; ez rendszerint a pólus iránya, amelyet a meridián illetve a meridiánkép érintője ad meg. Vegyünk fel most a vizsgált ponton kívül egy tetszőleges P pontot az alapfelületen, melynek képe P’ (???ábra). Az O-t és P-t összekötő geodéziai vonal O’P’ képének az O’-beli érintője általában nem esik egybe az O’P’ egyenessel; az általuk bezárt szöget második irányredukciónak nevezzük. Ennek nagysága a vizsgált O pontban az O’-beli érintőn kívül függ a P helyétől is.

A területtorzulási arányt az alapfelületi idom F felszínének és a képe F’ területének alapján számíthatjuk az alábbi képlettel:

A torzulási modulusok

A torzulási modulusok a torzulásokat a térkép egyes pontjaiban jellemzik, melyeket ezért határértékként definiálunk. Ezt szokás úgy is kifejezni, hogy nem véges nagyságú, hanem „végtelen kicsiny” mennyiségekre vonatkoznak.

Tekintsünk az alapfelület P pontján áthaladó sima görbét és azon egy másik Q pontot, valamint ennek a P’-n és Q’-n áthaladó képét. Ha a Q pont a görbe mentén minden határon túl megközelíti P-t, akkor az Ds-sel jelölt PQ ívből és a Ds’-vel jelölt P’Q’ ívből a

képlet adja az l hossztorzulási modulust vagy lineármodulust.

A vetületi egyenletek tulajdonságaiból következőleg a P pontban fellépő hossztorzulási modulus nem függ attól, hogy a Q pont a P-t milyen görbe mentén közelíti meg, hanem csak a görbe P-beli érintőjének irányától. Ezt úgy is fogalmazhatjuk, hogy a hossztorzulási modulus általában a hely és az irány függvénye. Ha a hossztorzulási modulus a térkép egy pontjából kiinduló minden irányban egységnyi, vagy egy vonal mentén egységnyi, akkor hossztartó pontról vagy vonalról beszélünk.

A szögtorzulási modulus definíciója megegyezik a szögtorzulási arányéval, vagyis az egymást metsző görbék érintője által bezárt alapfelületi d és képfelületi d' szögekre vonatkozólag:

(A határátmenetet itt az érintők mint a szelők határhelyzetei képviselik.) Ha a térkép egy pontjában bármely irányok különbségére i=1 –nek adódik, akkor a térkép e pontban szögtartó. Ha a térkép minden pontjában szögtartás áll fent, akkor szögtartó vetületről beszélünk.

Vegyünk most egy P pontot tartalmazó, Df felszínű felületdarabot az alapfelületen, melynek képe egy Df’ területű idom lesz a képfelületen. Zsugorítsuk rá a P pontra az alapfelületi idomot úgy, hogy minden pontja egyenletesen konvergáljon P-hez, miközben Df®0. Ha a

határérték létezik, akkor ezt nevezzük a területtorzulási vagy területi modulusnak. Ha a térkép egy pontjában t=1, akkor a térkép e pontban területtartó. Ha a térkép minden pontjában területtartás áll fent, akkor a vetületet területtartónak nevezzük.

A vetületek tehát a torzulásaik alapján lehetnek, szögtartók, lehetnek területtartók, de – amint azt a későbbiekben látni fogjuk – nem lehetnek egyidejűleg szögtartók és területtartók is. E két nagy torzulási csoporton kívül vannak még olyan vetületek, amelyeknél mind a szögek, mind a területek torzulhatnak; ezeket általános torzulásúaknak nevezzük.

Torzulásmentességről akkor beszélünk, ha a térkép valamely pontjában vagy valamely vonala mentén semmilyen torzulás sem lép fel, vagyis mind a hossztartás, mind a szög- és területtartás fennáll.

A vetületi torzulások kiszámítása

A következőkben egy adott vetületű térkép vetületi torzulásait kívánjuk kiszámítani valamely j,l koordinátákkal adott pontban. Tudjuk, hogy a hossz-, szög- és területtorzulásokat a torzulási ellipszis adatai szabják meg (???). Célunk tehát, hogy a vetületi egyenletek segítségével meghatározzuk az adott pontbeli torzulási ellipszis adatait. Ehhez szükségünk van közbeiktatott mennyiségekre, nevezetesen a fokhálózat menti torzulásokra.

Fokhálózat menti torzulások

A térkép egy pontjában a fokhálózat legfontosabb torzulási jellemzőit a fokhálózat menti torzulásokkal adjuk meg. Ezek:

- h parallelkör menti hossztorzulás

, ahol Dp a vizsgált pontot tartalmazó parallelkör menti ívdarab hossza, Dl a hozzá tartozó hosszúságmegváltozás, Dp’ pedig a megfelelő térképi ívdarab hossza;

- k meridián menti hossztorzulás

, ahol Dm a vizsgált pontot tartalmazó meridián menti ívdarab hossza, Dj a hozzá tartozó hosszúságmegváltozás, Dm’ pedig a megfelelő térképi ívdarab hossza;

- a fokhálózati vonalak képe által a térképen bezárt Q szög

(Megjegyezzük, hogy torzulási szempontból valójában nem a Q szög értéke, hanem ennek 90°-tól való eltérése lényeges. Ezt jobban kifejezi a ctgQ értéke, amelynek értéke annál jobban eltér 0-tól, minél jobban eltér Q a derékszögtől.)

E mennyiségek – mint majd az alábbiakban látjuk – közvetlenül kiszámíthatók a vetületi egyenletek segítségével, másrészről belőlük közvetlenül kiszámíthatók a torzulási ellipszis adatai.

A vetületi egyenletek és a fokhálózat menti torzulások összefüggései

Tekintsünk az alapfelületen egy P(j,l) pontot, és változtassuk meg ennek szélességét Dj-vel, hosszúságát pedig Dl-val, így kapjuk a P₁(j+Dj,l+Dl) pontot. Az eredeti és a megváltoztatott szélességek és hosszúságok egy kis foktrapézt határolnak (???ábra). Képezzük le ezt a foktrapézt a képfelületre; a vetületi egyenletek tulajdonságai miatt a foktrapéz oldalai közelítőleg egyenes szakaszokra képeződnek le, így eredményként közelítőleg négyszöget kapunk. Írjuk fel a Dj szélességmegváltozás és a Dl hosszúságmegváltozás eredményeként bekövetkezett Dx és Dy térképi koordinátaváltozásokat:

(Felhasználtuk a vetületi egyenletek folytonos differenciálhatóságát.) Hasonlóan kapjuk:

Az (???) ábráról látható tehát, hogy mind Dx, mind Dy egy (előjellel rendelkező) parallelkör irányú és egy meridián irányú megváltozásból adódik össze, amelyek a négyszög egy-egy oldalának a koordinátatengelyeken jelentkező merőleges vetületei. A szemközti oldalak merőleges vetületei mindkét tengelyen egyenlőnek tekinthetők, következésképpen egyenlő hosszúságúak, emiatt a foktrapéz képe közelítőleg parallelogramma.

Pythagoras tételét alkalmazva a parallelogramma oldalainak meghatározására kapjuk, hogy

Innen felírható a h parallelkör menti és a k meridián menti hossztorzulás:

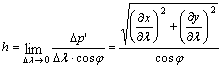
A fokhálózati vonalak által bezárt Q szöget írjuk fel azon és irányszögek különbségeként, amelyek a parallelogramma két oldala és az x tengellyel párhuzamos egyenes között keletkeznek (???ábra). Ekkor

Az ábra alapján a parallelogramma oldalairól és ezek x és y tengely irányú összetevőiről leolvashatók az alábbi összefüggések:

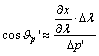
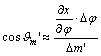
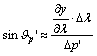
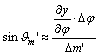
Ezeket behelyettesítve kapjuk ctgQ-ra Dj®0, Dl®0 esetén:

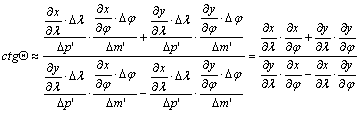
A fenti mennyiségekkel – az alapfelületi kis foktrapéz DF felszíne és a képfelületi kis parallelogramma DT területe segítségével – felírható a t területtorzulási modulus.

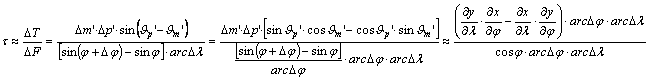(Itt felhasználtuk, hogy

.)

Egyszerűsítés után kapjuk a t területtorzulási modulusra, hogy Dj®0, Dl®0 esetén

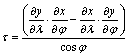
A vetületek jellemzése, osztályozása és elnevezése

A vetületek jellemzésének és osztályozásának főbb szempontjai:

- A leképezés alapfelülete lehet:

gömb, vagy

forgási ellipszoid;

- A vetület a perspektívitás azaz a centrális vetítéssel való előállíthatóság szerint lehet

perspektív;

nem perspektív;

- A perspektív leképezések képfelülete lehet

sík;

hengerpalást (többnyire forgáshenger-palást);

kúppalást (többnyire forgáskúp-palást);

- A térképi fokhálózat jellege szerint

valódi a vetület, ha

a) a parallelkörök képei vagy koncentrikus körök ill. körívek, vagy párhuzamos egyenesek, a meridiánok képei egy pontba összefutó vagy párhuzamos egyenesek, és a parallelkörök mindenütt merőlegesen metszik a meridiánok képeit; vagy

b) létezik olyan segédföldrajzi koordinátarendszer, amelyben a fenti három tulajdonság a segédparallelkörökre és a segédmeridiánokra teljesül.

képzetes a vetület, ha nem valódi, vagyis ha a fokhálózatra ill. a segédfokhálózatra a fenti három tulajdonság közül legalább az egyik nem teljesül.

- Az alkalmazott fokhálózat-elforgatás szögétől függően a vetület lehet transzverzális vagy ferdetengelyű, ha nem történt elforgatás, akkor normális; a perspektív vetületek esetén ezek az alap- és képfelület forgástengelye által bezárt szög szerinti elhelyezéseknek felelnek meg.

- A vetület torzulási besorolása (hogy t.i. szögtartó, területtartó vagy általános torzulású-e);

- A torzulásmentes hely vagy helyek megadása;

- a maximális torzulás (ha van ilyen) mértéke és helyének megadása;

A rendszeres vetülettanban a vetületeket elsődlegesen a fokhálózat jellege szerint szokás csoportosítani. További alapvető csoportosítási szempontot képeznek a torzulási tulajdonságok.

A térképek felhasználási területe is jelentősen befolyásolja a csoportosítást. A geokartográfiai (kis méretarányú) térképeknél kevés kivétellel gömb alapfelületet használnak, míg a topokartográfiában (a nagy méretarányú térképeknél) gyakorlatilag mindig forgási ellipszoid az alapfelület.

A vetületek elnevezése a csoportosítás és egyéb tulajdonságai alapján általában megadható (pl. „meridiánban és egyenlítőben hossztartó valódi hengervetület”, vagy „a ferdetengelyű, 30° és 60° segédszélességeken hossztartó, területtartó valódi kúpvetület a 45° szélességű és 0° hosszúságú segédpólussal”). Hogy ne kelljen ezeket a hosszú neveket használni, sok vetület megjelölésére használják a vetület megalkotójának vagy első alkalmazójának a nevét, vagy más rövid elnevezést (amely esetünkben a „négyzetes hengervetület”, vagy az „Albers féle kúpvetület”).