Számítási módszerek a térképészetben

Nem-lineáris egyenletek gyökének meghatározása

Nem-lineáris egyenletekkel gyakran találkozhatunk a térképészeti és a geodéziai számítások során. Egy ilyen egyenlet általánosságban

alakú, ahol h₁(x) és h₂(x) nem-lineáris függvények. Az egyenlet megoldása olyan gyök meghatározását jelenti, amelyet az egyenletbe helyettesítve, az egyenlőség teljesül:

Grafikusan az gyök a közös koordinátarendszerben ábrázolt

és az

függvények grafikonja metszéspontjának x koordinátájaként állítható elő (???ábra).

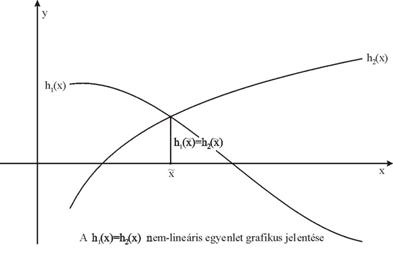
Célunk az egyenlet gyökének kívánt pontosságú numerikus előállítása.

Tekintsünk egy példát a nem-lineáris egyenletre. Ismert, hogy a forgási ellipszoidról gömbre történő szögtartó leképezésben (az ún. szögtartó gömbvetületben) az ellipszoidi F,L és a gömbi j, l koordináták között az alábbi egyenletek adják meg az összefüggést:

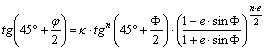
és

A szélességekre vonatkozó egyenletből a j gömbi szélesség kifejezhető:

,

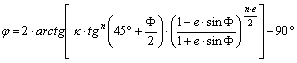a F ellipszoidi szélesség azonban nem írható fel explicit alakban a j gömbi szélesség függvényében. Ha adott j -ből kell F-t kiszámítanunk, akkor a geodéziai szakirodalom az egyenlet átrendezését ajánlja:

,

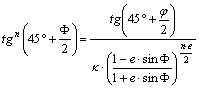majd a baloldali képletből a F kifejezését:

.

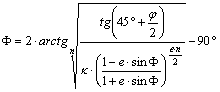Rögzített j gömbi szélesség mellett – a jobb oldali kifejezésbe a F ellipszoidi szélesség egy közelítését behelyettesítve – ez a képlet a F javított értékét eredményezi. Ezt az eljárást többször megismételve, az ellipszoidi szélesség egyre pontosabb közelítéseit kapjuk. Felmerül a kérdés, hogy mi biztosítja a fenti eljárás konvergenciáját (azaz hogy valóban egyre pontosabb és pontosabb közelítéseket kapunk), továbbá hogy más átrendezés esetén mikor várható hasonló eredmény.

Példa-egyenletünk bármely alakjában a F ismeretlen helyére x-et írva és j -t konstansnak tekintve, visszatérhetünk a bevezetőben alkalmazott jelölésre. A legutóbbi alaknál pl.:

,

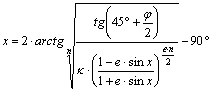vagyis ebben a

alakú egyenletben

és

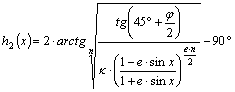
Visszatérve az általános alakhoz, a továbbiakban a

egyenletet rendezzük 0-ra:

A kiindulási egyenletünk megoldását tehát az f(x) nem-lineáris függvény zérushelyének meghatározására vezetjük vissza (???ábra).

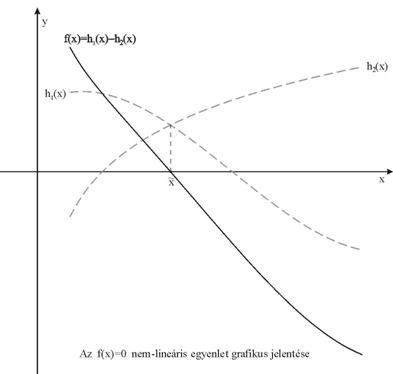
Az

egyenlet közelítő megoldására több módszer ismeretes. Ezek közül tekintünk át néhányat az alábbiakban.

A fokozatos közelítések módszere

Alakítsuk át az

egyenletet oly módon, hogy kifejezzük az egyenletből az x ismeretlent, ami többnyire megtehető. Az átalakított egyenletünk ekkor az alábbi alakú:

ahol g(x) 6nem-lineáris függvény. Képezzük ennek segítségével az x_i sorozatot az

képlet alapján. Ha ez a sorozat konvergens, akkor az -mal jelölt határértéke lesz az egyenlet gyöke, vagyis

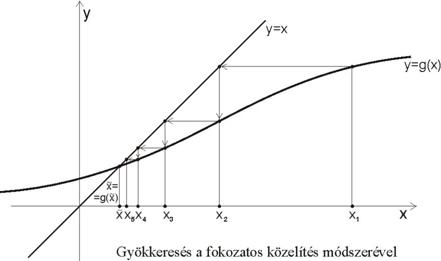
A konvergenciához elégséges feltételre van szükségünk. Tegyük fel, hogy az egyenletünk jobb oldalán álló g(x) függvény x₁ és között differenciálható, és

Ekkor – felhasználva a Lagrange féle középértéktételt:

,

ahol u az x_i és közé esik. Hasonlóan látható, hogy

.

Az eljárást -ig folytatva, teljes indukcióval látható, hogy

.

K<1 miatt Kⁱ®0, és ez a jobboldali kifejezés 0-hoz tartása miatt biztosítja a konvergenciát, vagyis:

.

Adjunk meg még egy korlátot az hibához a fenti elégséges feltétel fennállása esetére.

Induljunk ki ehhez a háromszög-egyenlőtlenségből:

A Lagrange-középértéktétel fenti következményéből adódik, hogy

A két egyenlőtlenség együttes alkalmazásából átrendezéssel következik, hogy

Kiemelés és átszorzás után:

Eszerint ha két egymást követő közelítés eltérése kicsi, akkor a közelítésünknek a gyöktől való eltérése is kicsi.

A fokozatos közelítések módszere nem mindig előnyös, mert egyrészt bonyolultabb egyenletek esetén x kifejezése az egyenletből hosszabb számolást igényelhet, másrészt a konvergencia elégséges feltételének biztosítása, illetve fennállásának ellenőrzése sem mindig egyszerű. A továbbiakban egyszerűbb módszert igyekszünk találni.

Gyökkeresés az intervallumfelezés módszerével

Ha egy intervallumon értelmezett folytonos f(x) függvényhez van olyan x₁ és x₂ pont, melyekben ellenkező előjelű értékeket vesz fel, vagyis

,

akkor Bolzano tétele miatt a függvénynek x₁ és x₂ között van zérushelye, amely gyöke az egyenletünknek:

Határozzuk meg az [x₁, x₂] intervallum x₃ felezőpontját:

Kivételesen előfordulhat, hogy éppen

,

és ezzel találtunk egy gyököt. Amennyiben viszont f(x₃)¹0, akkor vagy f(x₃)>0, vagy f(x₃)<0. A két fél-intervallum közül az egyikben biztosan kell lennie gyöknek, éspedig abban, amelynek végpontjaiban a függvényértékek különböző előjelűek. Ezt tovább felezve kapjuk az x₄ pontot (???ábra), stb.

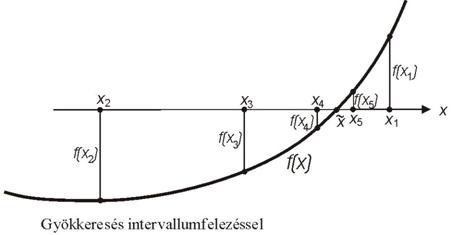
A gyököt biztosan tartalmazó intervallum hossza az i-edik felezés után:

Ez biztosítja az eljárás konvergens voltát. Az eljárást akkor tekinthetjük befejezettnek, ha az i-edik felezés eredményeképpen kapott intervallum hossza a megkívánt pontosságnál kisebb; a gyököt ekkor pl. ezen intervallum felezőpontjával közelíthetjük. Az eljárás azonban nincs tekintettel az f(x) függvény menetére, ezért konvergenciája lassú lehet.

A húrmódszer

Tekintsük ismét az

egyenletet, ahol f(x) folytonos. Az x₁, x₂ kezdőértékekre vonatkozólag itt is kikötjük, hogy álljon fenn az

egyenlőtlenség. A húrmódszer az intervallumfelezéses módszer javításának tekinthető annyiban, hogy az f(x) függvény görbéjének x₁, f(x₁) és x₂, f(x₂) koordinátájú pontjait összekötő egyenes metszi ki az x tengelyen az x₃ pontot (???ábra). A két ponton áthaladó egyenes egyenlete:

Ez egy lineáris függvény, melynek zérushelyét jelöljük x₃ –mal:

Az egyenletből x₃ kifejezhető:

Ez után x₁ és x₂ pontok közül azt tartjuk meg, amelyre igaz, hogy

(i=1,2) ,

a másik pontba x₃ értékét visszahelyettesítve, az eljárást a szükséges pontosság eléréséig ismételgetjük (???ábra).

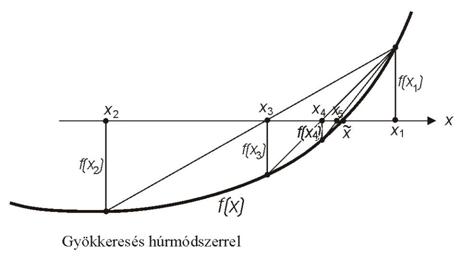
A konvergencia megfelelő feltételek mellett felgyorsítható. Ha ugyanis az [x₁, x₂] intervallumon teljesülnek az első és második derivált abszolút értékére az alábbi korlátossági feltételek:

(az f(x) szigorúan monoton), és

,

továbbá a

jelölés mellett feltesszük, hogy

,

akkor

,

tehát i®¥ esetén xi®.

A tétel belátásához vegyük az f(x) függvény másodfokú közelítését az [x₁, x₂] intervallumban. Ezt a másodfokú közelítést írjuk fel a lineáris l(x) függvény és egy másodfokú p(x) függvény összegeként (ahol l(x) az x₁, f(x₁) és x₂, f(x₂) koordinátájú pontokon áthaladó egyenes, p(x) pedig az x₁, x₂ végpontokban 0 értéket felvevő függvény):

ahol v0[x₁, x₂]. Ekkor az l(x) lineáris függvénynek az -mal jelölt gyökben felvett értéke egyrészt:

,

ahol w0[x₁, x₂], másrészt:

(Felhasználtuk itt Lagrange középérték-tétele mellett azt, hogy l(x₃)=0 és .)

A fenti két egyenletből kapjuk, hogy

A feltételek miatt

,

amiből adódik, hogy

Ehhez hasonlóan látható, hogy

(ahol i=1 vagy 2). Innen következik

Ennek analógiájára

(ahol j=i, azaz 1 és 2 közül valamelyik, vagy 3). Innen

stb., és ezzel a tételünket beláttuk.

A szelőmódszer

A húrmódszer kezdőpontjaiban a függvényértékek különböző előjelűeknek kell lenniük. A szelőmódszer a húrmódszer olyan módosítása, amely ezt kikerüli, és csak a kezdőpontokban felvett függvényértékek különbözőségét írja elő, továbbá a húrmódszernél általában gyorsabb konvergenciát biztosít.

Messe az x₁, f(x₁) és x₂, f(x₂) koordinátájú pontokat összekötő egyenes az x tengelyt az x₃ pontban (???ábra). Ezt – feltéve, hogy f(x₁)¹ f(x₂) – a húrmódszernél megismert képlettel kapjuk meg,:

Ez után – tekintet nélkül f(x₃) előjelére, de kikötve, hogy f(x₂) ¹ f(x₃) – hasonlóan kapjuk

f(x₄) –et. Általánosságban

ahol f(x_i-1) ¹ f(x_i) (???ábra).

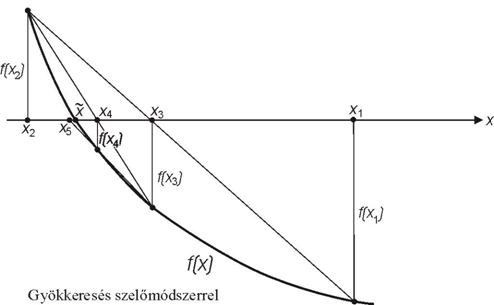
A szelőmódszer tehát – bár a konvergencia nincs mindig garantálva – általánosabb feltételek között alkalmazható, mint a húrmódszer. Emellett ha fennáll a konvergencia, akkor az a húrmódszerénél gyorsabb. Ennek belátásához induljunk ki a húrmódszernél kikötött feltételekből, vagyis mellett az [x₁, x₂] intervallumon legyen

és

,

továbbá

.

A kezdőértékre vonatkozó feltételünk miatt f(x₁)¹ f(x₂), ezért a fenti képletből kiszámítható x₃, amely megegyezik a húrmódszerből származó értékkel, és a szigorú monotonitás következményeként különbözik mind x₁-től, mind x₂-től. Továbbra is -mal jelölve a gyököt, a húrmódszernél látottak alapján kapjuk, hogy

és

,

innen pedig

.

f ’(x₃)¹0 miatt f(x₃) ¹ f(x₂), tehát a fenti képletből x₄ is képezhető. Az előbbiekhez hasonlóan látható, hogy

és ,

ezért x₃ ¹ x₄ , és a szigorú monotonitás miatt f(x₃) ¹ f(x₄) , tehát a fenti képlet alapján x₅ is képezhető. Továbbá

,

majd ugyanígy

.

(Megjegyezzük, hogy a húrmódszer konvergenciájának bizonyításában ezen a ponton x₃ helyett x_j áll, ahol j értéke lehet 1 vagy 2 is, és ebben az esetben csak annyit tudunk, hogy

.)

Ezt folytatva kapjuk, hogy

, stb.

Általában

,

ahol k₁=1, k₂=1, és k_i=k_i-2+ k_i-1 , ha i>2. Emiatt i>4 esetén k_i>i–1, q hatványai tehát i növelésével gyorsabban növekednek, ami biztosítja a gyorsabb konvergenciát.

Numerikus differenciálás és integrálás

Legyen példaként egy térképi vonalunk, és tekintsük ezt egy y=f(x) függvény grafikonjának. Ismeretes, hogy a differenciálható f(x) függvény-görbe xÎ[a,b] intervallumhoz tartozó s ívének a hosszát az

képlet adja meg. Ha tehát ismerjük az f(x) függvényt, akkor e képlet alapján határozhatjuk meg az s ívhosszat. A térképészeti gyakorlatban inkább az fordul elő, hogy az egyébként ismeretlen f(x) függvény értékeit bizonyos pontokban (például hosszméréssel) meg tudjuk állapítani, és ezekből az értékekből kell – közelítőleg – kiszámítani s értékét (???ábra).

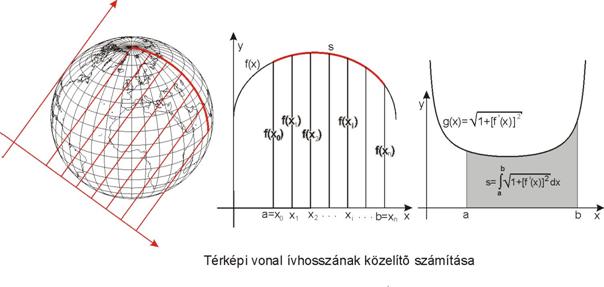
Általában adottnak tételezzük fel az ismeretlen f(x) függvény értékeit azon a=x₀, x₁, x₂, … , b=x_n pontokban, amelyek az [a,b] intervallum n részre (éspedig rendszerint egyenlő részekre) való felosztásából adódnak. Az s ívhossz mint integrál közelítőleg meghatározandó ezen x_i, f(x_i) (i=0,1, …, n) értékekből (???ábra).

A térképhasználat során a térképi hosszakon kívül egyéb térképi mennyiségek, pl. vetületi torzulások pontos kiszámításánál is szükségünk lehet függvények differenciálhányadosára és határozott integráljára, legalábbis ezek közelítő értékeire. A közelítő, másként numerikus differenciáláshoz és integráláshoz viszont a polinomos interpoláció alapjaiból indulunk ki.

Interpoláció alatt bonyolultabb függvényeknek egyszerűbb függvényekkel való közelítését értjük. Erre többnyire polinomokat használnak, de trigonometrikus függvények és racionális törtfüggvények felhasználása is előfordul. Tekintsük a polinomos interpoláció azon alkalmazását, amelynél az x₀, x₁, …, x_n pontokban adott f(x₀), f(x₁), …, f(x_n) függvényértékekhez keresünk a megfelelő pontokban ugyanazt az értékeket felvevő n-edfokú

polinomot (???ábra), vagyis:

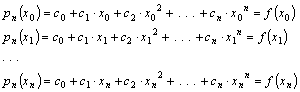
Ez egy n+1 egyenletből álló, n+1 ismeretlent tartalmazó lineáris egyenletrendszer a c₀, c₁, …, c_n együtthatókra mint ismeretlenekre nézve. Az egyenletrendszer determinánsa:

Ez egy ún. Vandermonde determináns, amely nem nulla, ha minden x_i különböző; az egyenletrendszer tehát egyértelműen megoldható. A c_i együtthatókat ki lehet számítani például a Cramer szabály alapján, de a gyakorlatban inkább más megoldásokat alkalmaznak.

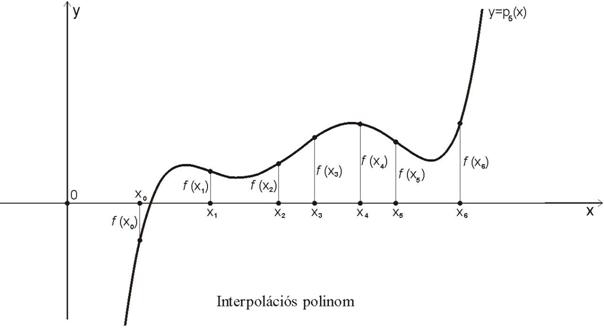
Állítsuk elő a szóbanforgó interpolációs polinomot Lagrange képletével, mely olyan n-edfokú a_i(x) -szel jelölt (i=0,1,2,…,n) polinomokból (az úgynevezett alappolinomokból) indul ki, amelyek az x_i pontban 1 értéket, az összes többi x_k pontban 0 értéket vesznek fel. Könnyen meggyőződhetünk róla, hogy az

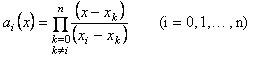
polinomok rendelkeznek mindezekkel a tulajdonságokkal. Az alappolinomok segítségével most már előállítható a p_n(x) interpolációs polinom, amely valóban átmegy az x_i, f(x_i)

(i=0, 1, …, n) koordinátájú pontokon:

Tekintsük pl. az x_i-1, f (x_i-1), az x_i, f(x_i) és az x_i+1, f(x_i+1) pontokon áthaladó másodfokú p₂(x) interpolációs polinomot:

A továbbiakban olyan interpolációs polinomokat fogunk használni, amelyeknél az x₀, x₁, …, x_n alappontok ekvidisztánsak, azaz egymástól egyenlő, h –val jelölt távolságra vannak (???ábra):

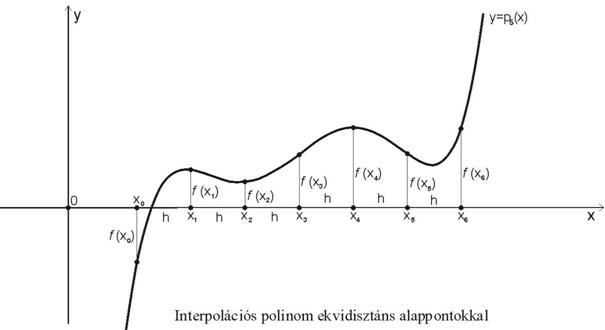
ahol

Ekkor az x_i-h, x_i, x_i+h pontokon átmenő másodfokú p₂(x) polinom az alábbi alakú:

illetve ugyanez a

vagyis az

helyettesítéssel:

(ahol x_i-h £ x £ x_i+h esetén -1 £ t £ 1) .

Ez utóbbi változatban a negyedfokú polinom a következőképpen néz ki:

Megjegyezzük, hogy az egymáshoz törésmentesen csatlakozó, legfeljebb harmadfokú interpolációs polinomokat, az ún. spline-okat a számítógépes grafikában is alkalmazzák.

Numerikus differenciálás

Célunk egy olyan, differenciálhatónak feltételezett f(x) függvény x_i pontbeli differenciálhányadosának közelítő meghatározása, amelynek f(x₀), f(x₁), …, f(x_n) értékeit csak egyes x₀, x₁, …, x_n pontokban ismerjük (???ábra). Ilyenkor a keresett differenciálhányadost az interpolációs polionom differenciálhányadosával közelítjük. Tételezzük fel, hogy a függvényérték az x_i-h, x_i, x_i+h helyeken sorra f(x_i-h), f(x_i), f(x_i+h). A három ponton áthaladó másodfokú polinom deriváltja a fentiek alapján:

A polinom deriváltja az x=x_i helyen:

Tehát a differenciálhányados közelítő értéke:

Többször differenciálható függvény esetén pontosíthatjuk ezt az eredményt pl. negyedfokú polinom alkalmazásával, amelyet az f(x_i-2h), f(x_i-h), f(x_i), f(x_i+h), f(x_i+2h) függvényértékekből számolunk a fenti képletből hasonló gondolatmenettel:

Végül a derivált az x=x_i helyen:

Kiemelés után innen kapjuk a differenciálhányados pontosabb közelítését:

Numerikus integrálás

Az f(x) függvény [a,b] intervallumon vett

határozott integrálját (ami szemléletesen a függvénygörbe alatti - előjeles - területtel egyenlő, ld. ???ábra):

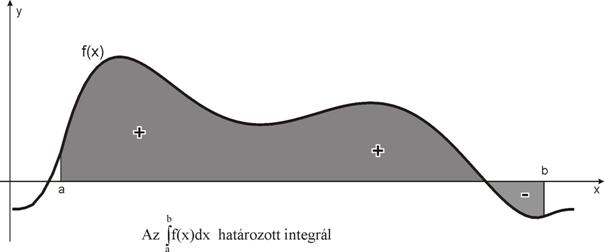
elméletileg pontosan ki lehet számítani a Newton-Leibnitz szabály segítségével:

ahol a F(x) függvény az integrálandó f(x) primitív függvénye:

.

Ha azonban a primitív függvény nem írható fel elemi függvények segítségével, vagy nem ismerjük, akkor numerikus integrálásra kerül sor.

Osszuk fel az [a,b] intervallumot n egyenlő részre, és jelöljük az osztásközök hosszát h-val:

.

Helyettesítsük az f(x) függvényt minden [x_i-1, x_i] (i=1, 2, …, n) osztásközben a lineáris interpolációs polinommal, vagyis az x_{i-1, f}(x_i-1) és az x_i, f(x_i) koordinátájú pontokat összekötő egyenes szakasszal (???ábra).

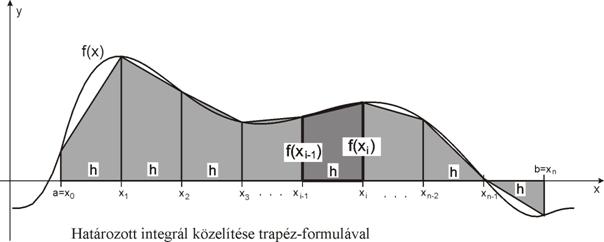
Ekkor függvény görbéje alatti terület a vizsgált osztásközben közelítőleg megegyezik egy olyan trapézzal, amelynél az alapok hossza f(x_i-1) és f(x_i), a trapéz magassága h=x_i-x_i-1. Az osztásközben számított határozott integrált a trapéz területével közelítjük:

A teljes integrált az így kapott rész-integrálok összegezésével kapjuk:

A megfelelő tagok összevonásából adódik, hogy

Ez az ún. trapéz-formula.

A határozott integrál definíciója alapján könnyen belátható, hogy az osztásközök n számának növelésével a trapéz-formula a határozott integrálhoz tart, ezzel együtt természetesen a képlet számítás-igénye is növekszik. Az [a,b] intervallumban kétszer folytonosan differenciálható f(x) esetén az adott n-hez megállapítható, hogy a

trapéz-összeg eléggé megközelíti-e az integrált. Bebizonyítható ugyanis a következő hibabecslő formula:

A jobb oldalon álló képletben az n kivételével minden konstans, így n értékének megfelelő megválasztásával a szükséges pontosság elérhető. A gyakorlatban azonban az f ’’(x) függvény [a,b] intervallumbeli maximumának meghatározása hosszadalmas lehet, ezért páros n esetén kiváltható az egyszerűbb

hibabecslő képlettel, ahol a minden második osztáspont elhagyásával kapott trapéz-összeg.

A trapéz-formula hátránya főleg akkor mutatkozik meg, ha a függvény az integrálási tartományban végig konvex vagy konkáv; ebben az esetben az egyes trapézokon keletkezett hibák halmozódnak.

Hatékonyabb integrál-közelítő összeget kapunk, ha az integrálandó f(x) függvény görbéjét az [a,b] intervallumon parabola-ívekkel közelítjük. Ennek alapfeltétele, hogy az [a,b] intervallum felosztásánál a rész-intervallumok n száma páros. Kettesével összepárosítva a rész-intervallumokat, az így kapott x_i-h, f(x_i–h), x_i, f(x_i), x_i+h, f(x_i+h) pontokhoz (az i páratlan) egy másodfokú interpolációs polinomot illesztünk (???ábra):

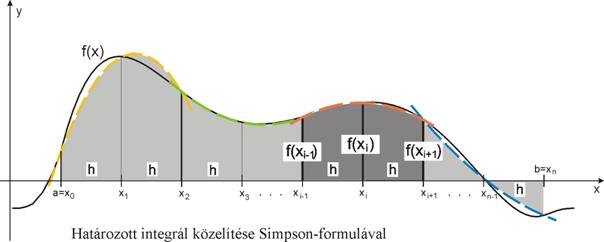
és ennek integráljával közelítjük az f(x) függvény integrálját az [x_i–h, x_i+h] rész-intervallumon:

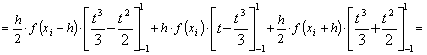
(Az helyettesítés következtében az integrandus -val szorzódott.)

A teljes [a,b] intervallumon vett integrál a rész-intervallumon vett integrálok összege, tehát

Az összevonások után kapjuk a Simpson-féle integrál-közelítő összeget:

Az előzőekhez hasonlóan a Simpson-formulából adódó s_n közelítő összegre is kapható hibabecslő formula. Négyszer folytonosan differenciálható f(x) függvény esetén belátható ugyanis, hogy

.

Ez a képlet a nevezőben álló n⁴ miatt azt mutatja, hogy – a feltételnek eleget tevő függvény esetén – a felosztás finomításával a közelítő összeg a trapéz-összegnél gyorsabban tart a határozott integrálhoz. Más szóval: megegyező számú osztáspont esetén a Simpson-formula jobb közelítést ad, mint a trapéz-formula. Az f ⁽⁴⁾(x) függvény [a,b] intervallumbeli maximumának meghatározási nehézségei miatt itt is előnyösebb egy közelítő hibabecslő képlet:

A Simpson-formula tehát kis mértékben bonyolultabb a trapéz-formulánál, de annál lényegesen hatékonyabb a határozott integrálok közelítő kiszámításában.