KARTOMETRIA A VETÜLETANALÍZISBEN

A térkép vetületének kiderítéséhez, a vetületi paraméterek vagy a névleges méretarány meghatározásához gyakran mérések elvégzésére is szükség van. Ezek többnyire hosszmérések, de szög- és területmérésekre is sor kerülhet. A kartometria általános megállapításai szerint legpontosabban a hosszakat tudjuk mérni, ezt követik pontosságban a szögmérések, míg a legnagyobb hiba a területmérésnél várható. Ezért minden mérést hosszmérésre célszerű visszavezetni, esetleg a területmérést hossz- és szögmérések kombinációjára. Végül közvetett módon a torzulások mérésére is sor kerülhet; ezt szintén hossz- és szögmérésre vezetjük vissza.

Hosszmérések

Hosszakat rendszerint fokhálózati vonalak mentén mérünk. E vonalak lehetnek egyenesek, körívek vagy egyéb görbék. A hosszmérés eredményeként kapott vetületi hossz és az alapfelületi hossz megfeleltetéséhez a vetület ismeretén kívül szükség van a névleges méretarányra, valamint a földgömb sugarára is. (Ez utóbbit általában 6371.1 km-nek vesszük.)

Egyenes mentén elvégzett hosszmérés

Egyenes szakasz hosszát elegendően pontos vonalzóval tizedmilliméter pontosságra olvashatjuk le. Ha a szakasz egyik végpontja nincs feltüntetve, vagy a térképszelvényen kívülre esik - pl. körív alakú fokhálózati vonalak sugarának meghatározásakor - akkor közvetett hosszmérésre kerülhet sor.

Valódi sík- vagy kúpvetületben egy szélességi kör képének r₁ sugarát a térképen teljes egészében ábrázolt (síktrapézra leképeződő) legnagyobb foktrapéz h₁ és h₂ húrjainak, valamint a szélességi körök m térképi távolságának segítségével állapíthatjuk meg (???. ábra). A határoló meridiánok és a húrok által képzett háromszögek hasonlóságából:

ahonnan átrendezés után:

Görbeív azonosítása

Az ívhossz-számítás módszere függhet a görbeív jellegétől, ezért azt megelőzően sor kerülhet a körív azonosítására. Más okokból a kúpszeletek azonosítására is szükségünk lehet. Mindkét esetben a görbe viszonylag távoli pontjai között kell húrt húznunk.

A körív esetében a húr felező merőlegese a görbét - a szimmetria miatt - mindig merőlegesen metszi. Ha a görbe különböző helyeken felvett húrjaira ez mindenütt teljesül, akkor feltételezhetjük, hogy körívvel van dolgunk. (A merőlegesség ellenőrzése helyett lehetséges a húrhoz a metszésponton keresztül párhuzamost húzni, és azt vizsgálni, hogy ez a metszéspontban érinti-e a görbeívet.)

A kúpszeletek azonosításához húzzuk meg egy görbeív A és B pontjait összekötő húr két végpontjában az érintőket, és ezek E metszéspontját kössük össze az AB egyenes H felezőpontjával. A HE egyenesnek a görbével való metszéspontját jelöljük C-vel (???. ábra). Az ellipszis minden húrjára HC<CE, a parabola minden húrjára HC=CE, a hiperbola minden húrjára HC>CE teljesül.

Ha egy görbeív minden húrjánál a HC<CE relációt tapasztaljuk, akkor a görbeívet elliptikusnak, HC=CE esetén parabolikusnak, HC>CE esetén hiperbolikusnak nevezzük. Ez önmagában még nem biztosítja, csak valószínűsíti, hogy éppen a megfelelő kúpszelettel van dolgunk, azonban a vetületeknél előforduló nem kúpszelet jellegű görbeívek (pl. a szinuszív) általában egyik csoportba sem sorolhatók be.

Körív mentén elvégzett hosszmérés

Ismert r sugarú és w középponti szögű körív s hossza:

Az w középponti szög nélkül is megadható az s ívhossz a húr h hosszának segítségével (???. ábra):

Ha sem r, sem w nem ismert, akkor a húr h hosszán kívül le kell mérjük annak a körívtől való maximális m távolságát is (???. ábra). Az ívnek a húrtól mért legtávolabbi pontját a húr végpontjával összekötő d hosszúságú szakaszra felező merőlegest állítva, két hasonló derékszögű háromszöget kapunk, innen:

; ezt átrendezve és Pythagoras tételét alkalmazva:

, ahonnan , végül

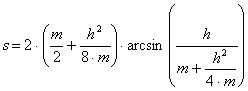
Ugyanez a képlet jó közelítéssel alkalmazható olyan kis görbületű görbeívek hosszának megadására, amelyeknél a húr h hossza az m maximális távolságnál sokkal nagyobb, és a görbeív nagyjából szimmetrikus alakú.

Az ábrázolt fokhálózati vonalak között elhelyezkedő pontokra vonatkozó mérések

A térképhasználati gyakorlatban mind a térképen ábrázolt fokhálózati vonalak között, valamely foktrapéz belsejében elhelyezkedő pont földrajzi koordinátáinak meghatározása, mind ismert koordinátájú pont térképre való felvitele előfordul. Normális elhelyezésű valódi vetületek esetében ez a feladat visszavezethető egyenes vagy körív mentén történő hosszmérésre. Ekkor ugyanis a meridiánok képe mindenképpen egyenes vonal, a parallelkörök képe pedig vagy egyenes vonal, vagy körív.

Legyen adott egy pont a térképen; keressük a földrajzi koordinátáit. Jelöljük a legkisebb tartalmazó foktrapéz közelebbi és távolabbi határoló szélességét j₀-lal és j₁-gyel, a határoló hosszúságait l₁-gyel és l₂-vel. Húzzuk meg a ponton áthaladó hosszúsági kör képét; ennek l hosszúságát a parallelkörök képeivel való metszéspontok helyzete adja lineáris interpoláció segítségével. A j szélesség első közelítését szintén lineáris interpolációból kapjuk.

Pontosabb értéket kaphatunk a j szélesség értékére, ha a többi szélességi kör helyzetét is figyelembe vesszük (ld. Érdi-Krausz megoldását [???]).

Azonosítatlan jellegű görbe vonal mentén történő hosszmérés

A fentiekben felsoroltakhoz nem tartozó görbék ívhosszának mérésénél a kartometria szokásos (körzős, fonalaslas, papírcsíkos, kurveométeres) módszerei a vetületanalízis során felmerült feladatokban nem elegendően pontosak. Ilyenkor a legpontosabb, de leghosszadalmasabb eljárásban a görbét egy alkalmilag felvett x,y koordinátarendszerben egy függvény grafikonjának tekintjük. Ismeretes, hogy az függvény [a,b] intervallumon vett grafikonjának s ívhosszát az

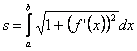
képlet adja meg.

Vegyünk fel egy x tengelyt, mégpedig úgy, hogy minden x értékhez a görbeívnek csak egy pontja tartozzon. (Ha ezt nem tudjuk megcsinálni, akkor a görbét ívdarabokra kell bontani.) A görbeív végpontjait merőlegesen rávetítve az x tengelyre, kapjuk az a és b pontot. Osszuk fel az [a,b] intervallumot (páros) n számú egyenlő részre, így kapjuk az x₀=a, x₁, x₂, …, x_n=b osztáspontokat. Mérjük le az x tengelyre merőlegesen adódó függvényértékeket, (lehetőleg az [a,b] intervallumon kívül még egy x_-1 és egy x_n+1 értéket hozzávéve). Közelítsük az x_i pontokban a differenciálhányadosokat a különbségi hányadosokkal:

Jelöljük a közelítő differenciálhányadosokból számított függvényértékeket p_i-vel:

Az integrál közelítését lehet pl. a Simpson-formula segítségével végezni:

ahol

Az ívhossz egy másik, a p_i értékek első és második differenciáin alapuló képletét Érdi-Krausz idézett művében találjuk.

Szögmérés

A térképeken végzett mérések során szükségessé válhat egymást metsző egyenesek vagy görbék által bezárt szögek nagyságának meghatározása.

Egyenes szögszárak esetén a legpontosabb eredményt akkor várhatjuk, ha a szögmérést - a szögszárak hosszának és végpontjaik távolságának megállapításával és a síkháromszögekre vonatkozó koszinusz-tétel alkalmazásával - hosszmérésre vezetjük vissza. Kevésbé pontos eredményt ad a szögmérő használata.

Gyakran előfordul, hogy olyan egyenesek (pl. meridiánok) szögét keressük, amelyek metszéspontja a térképlapon kívül van. Hosszmérés segítségével meghatározzuk a térképen ábrázolt legnagyobb foktrapéz határoló szélességi köríveihez tartozó húrok s₁ és s₂ hosszát, valamint az m oldalhosszat (???. ábra). Hasonló háromszögekből adódik, hogy a keresett Dl szöget a

képlet szolgáltatja.

Kisebb pontossági igény esetén egy háromszögvonalzót egyik élével az egyik meridián mellé helyezve és egy másik vonalzó mentén a másik meridiánnal való metszésig eltolva párhuzamost húzhatunk, így a szög már megmérhető.

Görbe vonalak metszéspontjában a szöget az érintők által bezárt szöggel definiáljuk. Az érintő szemmértékkel történő felszerkesztése nem elég pontos, ezért inkább normálist célszerű szerkeszteni. Ehhez szükségünk van egy fényes felületű fém vagy műanyag vonalzóra, amelyen a görbe tükörképe jól látható. Helyezzük a vonalzót a metszéspontban élével közelítőleg merőlegesen a görbére (!!!. ábra). Ha a vonalzó pontosan merőleges, akkor a görbe és a tükörképe simán megy át egymásba, ellenkező esetben a vonalzó szélén töréspont keletkezik. A vonalzó elforgatásával a sima átmenetet létrehozva, a normális meghúzható. A keletkező törésszögnél a derékszögtől való eltérés kétszerese látszik, így a normálist fele akkora hibával tudjuk felszerkeszteni, mint az érintőt.

Területmérés

A területmérés adja a legkevésbé pontos eredményt, ezért erre a gyakorlatban viszonylag ritkán kerül rá sor. Egy térképi idom területének nagyságát igyekszünk inkább hosszméréssel, vagy hossz- és szögmérés kombinációjával meghatározni. Ha ez nem lehetséges, vagy gyorsabban akarunk eredményt elérni, akkor más módszer után kell néznünk.

A legegyszerűbb, bár hosszadalmas a négyzethálóval (pl. milliméterpapírral) való leborítás és a határon belülre eső négyzetek leszámolása. Itt a határra eső négyzetek figyelembevétele okozhat gondot. Ha egy négyzet területének több mint a fele az idomhoz tartozik, akkor belső négyzetnek, fordított esetben küldő négyzetnek célszerű tekinteni.

Végső soron hosszmérésre vezet vissza az Alder-hárfa vagy ehhez hasonló elvű más eszköz alkalmazása. Ekkor a lemérendő területű idomot egymástól egyenlő távolságra húzódó párhuzamos vonalak rendszerével borítjuk, és így azonos magasságú, közelítőleg trapéz alakú részekre bontjuk. Valamilyen hosszmérési módszerrel lemérjük a közelítő trapézok középvonalát, majd e hosszakat összeadva és a magassággal beszorozva, kapjuk a területet.

Mind a négyzethálós, mind a hárfás módszer pontosságát javíthatjuk, ha a párhuzamos vonalrendszerünket egy hegyesszöggel elforgatva az eljárást megismételjük, és az így kapott területeket átlagoljuk.

Viszonylag gyors, ugyanakkor aránylag pontos eredményt ad a polárplaniméter használata. Egy zárt görbe által határolt területet tudunk meghatározni oly módon, hogy az eszközzel a kontúrja mentén körüljárjuk.

A polárplaniméter két, forgástengellyel összekötött fémlécből áll: a térképen rögzített végű p lécből és a kontúron körbevezetett végű r lécből. A p léc egyik végén lévő O-tű, az ún. pólus a műszer rögzítésére szolgál, a másik vége az A forgástengely, amely az r léccel kapcsolja össze (???. ábra). A műszer legfontosabb része az r léccel összekötött C görgő, mely egy, az r léc tengelyével párhuzamos tengely körül foroghat. Tengelyirányú elmozdulásnál C nem forog, csak csúszik.

A mérés alapja az az állítás, hogy a kontúr egyszeri körüljárásakor a megmérendő területe lineáris függvénye a C görgő u elfordulásának. Ennek belátásához először tegyük fel, hogy az O pólus a kontúron kívül helyezkedik el (???. ábra). A kontúr B pontjában van a vezetőcsúcs. Jelölje p₀ az OA távolságot, r₁ az AB távolságot, r₀ az AQ távolságot, ahol a Q pont a C görgő merőleges vetülete az r lécen.

Toljuk el a vezetőcsúcsot a kontúr mentén a közeli B₁ pontba. Eközben az r léc helyzete úgy változik meg, hogy egyenese az eredeti helyzet egyenesét a Q pontban metszi, az A pont az A₁ pontba, a Q pont a Q₁ pontba kerül át. Jelöljük az AOA₁ szöget Da-val, a B₁QB szöget Dj-vel, a QQ távolságot x-vel.

Számítsuk ki azt a DT területet, amelyet az OAB töröttvonal súrol, amíg a B pont B₁-be kerül. DT közelítőleg három részre bontható: az AOA₁ háromszögre (DT₁), az AA₁B₁D trapézra (DT₂), és az ADB háromszögre (DT₃). Figyelembe véve, hogy B₁ (és ezzel együtt D is) közel van B-hez, ezért Da és Dj kicsi. A háromszögeket így körcikkel, a trapézt parallelogrammával helyettesíthetjük:

, és

Tehát

ahol a ívdarab a C görgő elfordulása.

Ha teljesen körüljárjuk a kontúrt, akkor - elévégezve a részterületek összegezését és egy határátmenetet - az OAB töröttvonal által súrolt egész T terület (előjelhelyesen):

ahol a C görgő teljes (előjelhelyes) elfordulása.

A teljes körüljárás után , tehát , azaz T arányos a C görgő u elfordulásával.

Most már csak azt kell belátni, hogy T a megmérendő idom területe. Ez nyilvánvaló, hiszen egy körüljárásnál az OAB töröttvonal egy bizonyos területet súrol. Ebben a területben a kontúron kívül szereplő rész kétszer szerepel. Egyik irányban való elmozdulásnál pozitívnak (Da>0, Dj>0), ellenkező irányban való elmozdulásnál negatívnak (Da>0, Dj>0) adódik, azaz ezek egymás ellentettjei, így az összegezésnél kiesnek.

Hasonló meggondolással látható, hogy ha az O pólus a kontúron belül van, akkor

és

A lemérendő idom T területe tehát valóban lineáris függvénye a C görgő u elfordulásának.

Megjegyezzük, hogy a planiméterre jellemző állandókat valamilyen ismert terület lemérésével lehet meghatározni.

A torzulások mérése

Ismeretlen vetületű térképen, amelyen van fokhálózat, a torzulások közelítőleg meghatározhatók mérések segítségével, mégpedig a torzulási ellipszis adatain keresztül. Érdi Krausz eljárását követve [???], válasszunk ehhez egy olyan fokhálózati metszéspontot, amelyet tartalmazó legkisebb foktrapéz, de legalábbis a pontból kiinduló négy fokhálózati ívnek a foktrapézba eső része a térképen teljes egészében rajta van (???. ábra). A P₀ (j₀,l₀) pontot tartalmazó legkisebb foktrapézt határolja délről a j₁, északról a j₂ szélesség, nyugatról a l₁, keletről pedig a l₂ hosszúság. A j₀ szélességi körön a l₀ hosszúságtól a l₁ illetve a l₂ hosszúságig terjedő parallelkör-ívet jelöljük e₁-gyel illetve e₂-vel; a l₀ hosszúsági körön a j₀ szélességtől a j₁ illetve a j₂ szélességig terjedő meridiánívet jelöljük t₁-gyel illetve t₂-vel. Az e₁, e₂, t₁ és t₂ hosszakat a görbületük mértékétől függően általában körívként vagy egyenesként mérjük le. Jelöljük e₁ és e₂ átlagát De -vel, t₁ és t₂ átlagát pedig Dt -vel:

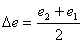és .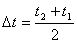

Legyen továbbá

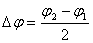és .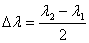

Ha R a földgömb sugara, M pedig a névleges méretarány-szám, akkor a fokhálózat menti hossztorzulásokat az alábbi módon becsülhetjük:

és

.

A (j₀,l₀) pontban a fokhálózati vonalak érintője által bezárt Q szög a fentiekben leírt módon megmérhető, így már rendelkezésünkre állnak a fokhálózati torzulások közelítő értékei. A következő lépésben kapjuk a torzulási ellipszis nagy- és kis-féltengelyeit:

és

.

Végül számítjuk az első vetületi főirány és a meridián illetve a parallelkör érintője által az alapfelületen bezárt u illetve v szöget, valamint ezeknek térképi megfelelőjét, a torzulási ellipszisnek a meridián- illetve parallelkör-kép érintője által bezárt u’ illetve v’ szöget:

és

,

valamint

és

.

Az eredményeket az és képletek alapján ellenőrizhetjük.

A kiszámolt mennyiségekből a torzulási ellipszis a térképre felszerkeszthető.

A t területtorzulási modulust a képletből kapjuk meg. Ahol t»1 (3-4%-os eltéréssel), ott területtartást feltételezhetünk. Ha a térképünkön mindenütt t»1, akkor valószínűleg területtartó vetülettel van dolgunk.

A szögtorzulást leginkább a második irányredukció maximumának kétszeresével jellemezzük:

Ahol a»b (3-4%-nál kisebb eltérés megengedhető), ott alighanem szögtartás áll fent. Ha a térképünkön mindenütt a»b, akkor a vetület nyilván szögtartó.

a és b értékei a maximális és a minimális hossztorzulást adják meg, melyek a vetületi főirányok irányában lépnek fel. Ha más irányú hossztorzulásra van szükségünk, akkor tudnunk kell, hogy ez a J’ irány milyen szöget zár be az első vetületi főiránnyal. Tudjuk, hogy ekkor a megfelelő alapfelületi J irány a

képletből adódik. Ebben az irányban a hossztorzulási modulust a

képlet adja (1-2%-os eltérés pontossággal).

Ha a<1<b , akkor van olyan irány, amelyben nincs hossztorzulás. Ennek az iránynak a kiderítése (pl. a hossztartó vonal meghatározásának céljából) a

egyenlet J-ra való megoldásával lehetséges.