Mind a geo-, mind a topokartográfiai térképek vetületével szemben alapvető elvárás, hogy az ábrázolás témájára nézve leghátrányosabb torzulások ne lépjenek fel, vagy a lehetőség szerinti legkisebbek legyenek. Ennek elbírálása céljából egyértelmű összehasonlíthatósági módszert kell találnunk az ugyanazon területet több különböző vetületben ábrázoló térképekhez: el kell tudnunk dönteni, hogy a torzultság vonatkozásában melyik vetület a legelőnyösebb. A torzultság fogalmát itt nem lokálisan, hanem globálisan, nagyobb térségre kiterjedően értjük.

• ki kell jelölni a számunkra lényeges, vagyis a tematika szempontjából különösen hátrányos torzulást (pl. hossz-, szög-, terület-, stb.);
• ennek alapján a torzultságot (vagyis a torzulásmentes állapottól való eltérés nagyságát) meg kell határozni az ábrázolt terület minden részére kiterjedő, minél több pontban;
• ezeket a torzulási mennyiségeket ki kell értékelni oly módon, hogy minden egyes vetülethez egyetlen (nem-negatív) számérték legyen hozzárendelhető, amely a torzultságot összességében jellemzi.

A térkép pontjaiban fellépő lokális torzultsági értékek együttes figyelembevételére a szakirodalom két lehetőséget kínál:

• A minimax elv szerint - a leggyengébb láncszemhez hasonlóan - a térkép torzultságát a rajta fellépő legnagyobb torzultsággal jellemezzük; azt a vetületet tekintjük tehát legjobbnak, amelynél a torzultsági értékek maximuma a legkisebb. Ennek alkalmazására akkor kerül sor, ha a térképen egy bizonyos korlát alatt maradó torzulásokat figyelmen kívül kívánjuk hagyni. A nagyméretarányú, közvetlen mérésekre is használt térképeknél a mérési eredményeket a névleges méretarány segítségével számítjuk át valódi méretekre, a vetületi torzulásokról nem veszünk tudomást. A torzultság globális megítélése a topokartográfiai térképek körében tehát célszerűen a minimax eljáráson alapul.
• A variációs elv szerint az a vetület tekintendő a legelőnyösebbnek, amelynél a torzultsági értékek átlaga a legalacsonyabb. A kisméretarányú, kiterjedt térségeket ábrázoló térképeknél számolni kell azzal, hogy a torzultságok erősen megnövekednek, helyenként a végtelenhez tartanak. A torzultságok maximumának vizsgálata itt értelmetlen; elvárhatjuk viszont, hogy a torzultságok átlaga legyen minél kisebb. A geokartográfiai térképek globális torzultságát tehát a variációs eljárás segítségével hasonlítjuk össze. (A “variációs” elnevezés onnan ered, hogy a torzultság átlagának minimalizálása matematikailag variációszámítási feladat megoldására vezet.)

Ha nem véges számú vetület torzultságát hasonlítjuk össze egy rögzített T ábrázolási tartományon, hanem egy végtelen sok elemből álló vetülethalmaz legelőnyösebb globális torzultságú vetületét keressük ugyanitt, akkor optimális torzulású vetületről beszélünk. Ha az összes elméletileg létező vetület közül választjuk ki a minimális torzultságút, akkor kapjuk az ún. ideális vetületet; ha egy körülhatárolt vetületcsoportból választjuk ki a minimumot, akkor kapjuk az ún. legjobb kartográfiai vetületet. A geokartográfia körében a vetületválasztásnál általában előzetes elvárásokat fogalmazunk meg a vetületi jelleggel és a torzulásokkal szemben; ezek leszűkítik a számításba jövő vetületek körét. A gyakorlatban tehát az egyébként is bonyolultan meghatározható ideális vetület helyett inkább a legjobb kartográfiai vetületeket keressük.

Az ábrázolandó T tartományon az átlagos torzultságot az e ² lokális torzultsági mutatószám felületi integráljával számítjuk ki:

ahol m ( T ) a T tartomány felszínét jelöli, mely elvileg bármilyen szabálytalan alakú terület is lehet, azonban a számítások egyszerűsítése érdekében előnyben részesítjük a szabályos tartományokat, ezek között is gömböveket, gömbsüvegeket, illetve általános helyzetű foktrapézokat.

A valódi vetületeknél - normális elhelyezés esetén - a fokhálózati vonalak vetületi főirányok, ezért a h és k fokhálózat menti hossztorzulások megegyeznek az a maximális és b minimális hossztorzulással. Ebből adódóan e ²(a,b)=e ²(h,k).

A valódi hengervetületeknél és . Emiatt az átlagos torzultság a j _D, j _É szélességi körökkel és a l _Ny,l _K hosszúsági körökkel határolt foktrapézon:

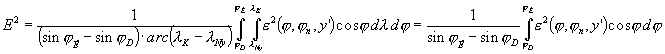(Figyelembe vettük, hogy az integrandus nem függ l -tól.)

Keressük azt az y vetületi egyenletet és azt a j _n normálszélességet, amely mellett az átlagos torzultság a legkisebb lesz. (A másik vetületi egyenlet mindig alakú.)

Szögtorzultság vizsgálata esetén az egyenlettel megadott szögtartó hengervetület lesz a legjobb, mert torzultsága zérus. Az optimális j _n normálszélességet egyéb szempontok alapján választhatjuk ki.

Területtorzultság vizsgálata esetén az egyenlettel megadott területtartó hengervetület lesz a legjobb, mert torzultsága zérus. Az optimális j _n normálszélességet itt is egyéb szempontok alapján választhatjuk ki.

A valódi síkvetületeknél és , ahol q=q(b ) a sugárfüggvény, az ábrázolandó területet a pólustól a b _H pólústávolságú határoló szélességig terjedő gömbsüveg. Innen az átlagos torzultság:

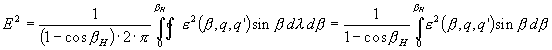
(Figyelembe vettük, hogy az integrandus itt sem függ l -tól.)

Keressük azt a q sugárfüggvényt, amely mellett az átlagos torzultság a legkisebb lesz.

Szögtorzultság vizsgálata esetén a sugárfüggvénnyel megadott szögtartó (sztereografikus) síkvetület lesz a legjobb, mert torzultsága zérus. (b _n itt a metszési parallelkört jelöli, amelynek optimális értéke egyéb szempontok alapján választható ki.)

Területtorzultság vizsgálata esetén az sugárfüggvénnyel jellemzett területtartó síkvetület lesz a legjobb, mert torzultsága zérus.

Teljes torzultság vizsgálata esetén - minden kritériumra - a legjobb vetületnél a vetületi kezdőpontban a meridián mentén hosszrövidülés lép fel (h< 1 ), innen kifelé haladva a parallelkörök ritkulnak, és a meridián menti hossztorzulás a határoló parallelkörnél éri el az egységnyi értéket.

A valódi kúpvetületeknél és , ahol p=p(b ) a sugárfüggvény, n a sugárhajlás, az ábrázolandó terület pedig a b _É és b _D pólustávolságú parallelkörök, valamint a l _Ny és l _K meridiánok által határolt foktrapéz. Innen az átlagos torzultság:

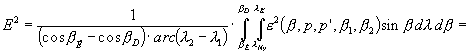
ahol b ₁ és b ₂ a két normálparallelkör; határhelyzetben b ₁=b ₂=b _n . (Figyelembe vettük, hogy az integrandus itt sem függ l -tól.)

Keressük azt a p sugárfüggvényt és n sugárhajlást, amely mellett az átlagos torzultság a legkisebb lesz.

Szögtorzultság vizsgálata esetén a sugárfüggvénnyel megadott szögtartó kúpvetület lesz a legjobb, mert torzultsága zérus. Ha egyetlen b _n normálparallekört írunk elő, akkor

és n=cosb _n .

és .

Ekkor b ₁ és b ₂ optimális értéke egyéb szempontok alapján választható ki.

Területtorzultság vizsgálata esetén a

sugárfüggvénnyel megadott területtartó kúpvetület lesz a legjobb, mert torzultsága zérus.

Ha (Lambert féle) póluspontos vetületet akarunk, akkor p_p=0 és

, ahol a b _n optimális értéke egyéb szempontok alapján választható ki.

Ha pólusvonalas vetületre van szükségünk, akkor

és .

Ehhez a b ₁ és b ₂ optimális értéke egyéb szempontok alapján választható ki, amelyek egybe is eshetnek: b ₁=b ₂=b _n . Ekkor b ₁ és b ₂ , illetve b _n optimális értéke egyéb szempontok alapján választható ki.

Átlagos hossz- és teljes torzultság vizsgálata esetén – tekintetbe véve, hogy kúpvetületet ritkán használunk nagyobb terület ábrázolására – a legjobb vetület csak csekély mértékben különbözik a meridiánban hossztartó kúpvetülettől. Ezért a gyakorlatban a de l’Isle féle vetület megfelelő közelítést ad a legjobb kúpvetületre:

Ha egyetlen b _n normálparallekört írunk elő, akkor

és n=cosb _n ;

és .

Ilyenkor csak b ₁ és b ₂ , illetve b _n optimális kiválasztása a feladat.

A képzetes vetületek torzulási képletei bonyolultabbak, ezért a legjobb képzetes henger-, kúp- és síkvetületek egzakt meghatározása hosszadalmas számításokat igényel. A vizsgálat egyik lehetséges leegyszerűsítése, hogy nagy számú képzetes vetületnek ugyanazon ábrázolási tartományra vonatkozó átlagos torzultságát kiszámítjuk, és ezek alapján hasonlítjuk össze illetve rangsoroljuk őket.

Amikor az ábrázolási tartomány az egész Földre kiterjed, akkor a pólusoknál fellépő végtelenhez tartó torzultságok miatt T-t úgy választjuk meg, hogy a két pólusnál egy-egy 5°-os sugarú gömbsüveg torzultsági értékeit nem vesszük figyelembe; vagyis T ilyenkor a 85° D-i és a 85° É-i szélességi körök közé eső gömböv. Az egész Földet ábrázoló, a gyakorlatban előforduló fontosabb képzetes vetületeket az átlagos teljes torzultságuk alapján vizsgálva, az egyes kritériumok a számításba vett vetületek különböző rangsorait adják. A rangsorok alapján az alábbi általános észrevételek tehetők:

• A rangsorok elejére inkább általános torzulású vetületek kerültek, megelőzve a területtartó vetületeket és különösen a néhány szögtartó vetületet;
• A rangsorok elejére az elsődleges vetületekkel szemben azok megfelelően átszámozott változatai kerültek, Aitoff átszámozott vetületei több kritérium szerint is a legjobbnak bizonyultak;
• Az elsődleges vetületek közül Winkel vetülete, a CNIIGAiK pszeudopolikónikus vetülete, Baranyi IV. és Kavrajszkij II. (elliptikus) vetülete minden rangsorban a legjobbak között szerepel;
• A polikónikus vetületek, Bonne és Van der Grinten vetülete minden rangsorban a leggyengébbek között szerepel.

A kiszámított viszonylag nagy számú torzultsági mérőszám lehetővé teszi a statisztikai elemzést. Az egyes kritériumok közötti korrelációs együtthatók azt mutatják, hogy igen szoros korreláció áll fent a Jordan féle és az Airy-James-Clarke kritérium, valamint – magától értetődően - az eredeti és a módosított Airy kritérium értékei értékei között. Valamivel gyengébb, de még mindig szoros a korrelációs összefüggés utal a Jordan-Kavrajszkij és az Airy-Kavrajszkij kritérium rokonságára.

Az egyéb képzetes vetületeknél nincsen a vetület jellegére, matematikai sajátosságaira vonatkozó kikötés, ezért ebben a körben a legjobb kartográfiai vetület már megegyezik az ideális vetülettel.