TORZULÁSI ARÁNYOK, TORZULTSÁGI KRITÉRIUMOK

A torzulási arányok

A torzulási modulusok egy pontra vonatkozólag, határérték formájában adtak a torzulási viszonyokról információt. A térképek használata során azonban inkább véges kiterjedésű idomok torzulását szeretnénk ismerni. Meghatározott nagyságú térképi idomok méretét elosztva a megfelelő alapfelületi idom méretével, kapjuk az ún. torzulási arányt. Ezek kiszámítása végső soron visszavezethető a torzulási modulusokra. A következőkben a hossztorzulási arány és a területtorzulási arány meghatározásával fogunk foglalkozni. A szögtorzulási modulus maga is véges idomokra vonatkozik, így a torzulási arány fogalmát rá nem szükséges külön értelmezni.

Hossztorzulási arány

Egy egydimenziós alapfelületi objektumnak tekintett véges hosszúságú vonal l hossztorzulási arányát úgy kapjuk meg, hogy az S’ vetületi ívhosszat osztjuk az S alapfelületi ívhosszal:

Az alapfelületi vonal pontjait megadhatjuk pl. [j(t),l(t)] paraméteres alakban, ahol j(t) és l(t) legyen a t paraméter differenciálható függvénye, és jelöljük P‑vel a kezdőpontot. Minthogy az alapfelületi vonal ívhosszának kiszámítási módja nem befolyásolja a hossztorzulást, választhatjuk egyszerűség kedvéért az ún. természetes paraméterezést, vagyis t legyen a kezdőponttól a . [j(t),l(t)] koordinátájú pontig terjedő görbeszakasz ívhossza. Osszuk fel most az S hosszúságú alapfelületi vonalunkat kis darabokra, Dt_i-vel jelölve a paraméter megváltozását. Ez a térképi vonalon is generál egy felosztást (???ábra). Egy kis alapfelületi ívdarabhoz a térképen - x=x(j,l) és y=y(j,l) vetületi egyenletek mellett - Dx_i , Dy_i koordinátamegváltozások tartoznak. A térképi osztáspontokat egyenes szakaszokkal összekötve egy töröttvonalat kapunk, amelynek hossza alulról közelíti az S’ térképi ívhosszat:

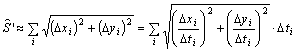
Az alapfelületi vonal felosztásának minden határon túli finomítása esetén egyrészt a töröttvonal hossza a térképi S’ ívhosszhoz tart, másrészt a fenti összeg egy integrálba megy át, tehát:

(Itt figyelembe vettük, hogy x és y t-nek közvetett függvénye, és felhasználtuk a többváltozós függvényekre vonatkozó láncszabályt.)

Ebben a képletben a gyökös kifejezés az alapfelületi vonal minden pontjához éppen az érintő irányában fellépő hossztorzulási modulust adja meg. Látható tehát, hogy a vonal vetületi hossza a hossztorzulási modulus vonalintegrálja.

Az S’ vetületi hossz ismeretében a vonal l hossztorzulása elméletileg:

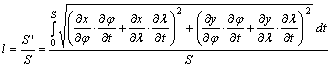
A hossztorzulási arány ezek szerint a vonal mentén fellépő hossztorzulási modulusok átlaga.

A gyakorlatban ezt a legáltalánosabb formulát nemigen használjuk, mert a bonyolultan haladó alapfelületi vonalak torzulását nem számítjuk ki közvetlenül. Viszont ahogyan egy síkgörbe tetszőleges pontossággal megközelíthető töröttvonallal, úgy bármely (rektifikálható) alapfelületi vonal megközelíthető egymáshoz csatlakozó ortodrómaívekkel. Ezért elegendő a két végpontot az alapfelületen összekötő legrövidebb vonal (esetünkben gömbi főkörív) hossztorzulását vizsgálni. A gömbháromszögtan tételei alapján ekkor a vonal S hossza:

ahol j₁ és j₂ a végpontok szélességei, Dl pedig a hosszúságkülönbségük. Pontosabban: l₁, l₂ -vel jelölve a végpontok hosszúságait, ha az ortodróma nem metszi a 180°‑os meridiánt, akkor

Dl=l₁-l₂ , ellenkező esetben pedig Dl=(360°-|l₁-l₂|)×sign(l₁-l₂) . Ezt felhasználva:

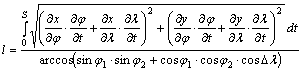
A számlálóban az alapfelületi ortodróma j(t), l(t) alakban felírt paraméteres egyenletének deriváltjai szerepelnek. Lényegesen leegyszerűsíthető lenne ez a képlet, ha az alapfelületi ortodróma a térképre egyenes szakaszként képeződne le. Tudjuk, hogy ez csak a gnomonikus síkvetület esetén teljesül, azonban nagyméretarányú térképeken a görbültség gyakorlatilag nem észlelhető. (Az utóbbi évtizedekben közepes és kisebb méretarányokban is közkedveltté vált Lambert‑Gauss féle szögtartó kúpvetületben nagyjából egyenesnek tekinthetők a 3000 km‑nél nem hosszabb ortodrómák képei.) A térképhasználók túlnyomó többsége ‑ méretaránytól és vetülettől függetlenül ‑ a térképi távolságmérésnél a görbültséget egyébként is figyelmen kívül hagyja. Ez alapján a hossztorzulás bizonyos esetekben közelíthető az alábbi képlettel:

(x₁ , y₁ és x₂ , y₂ a végpontok vetületi síkkoordinátái.)

Területtorzulási arány

Egy véges kiterjedésű alapfelületi T tartomány területtorzulási arányát úgy kapjuk meg, hogy az idom térképi területét osztjuk az alapfelületi felszínnel. Jelöljük T felszínét m(T)-vel, T képének térképi területét pedig n(T)-vel. A t területtorzulási arány tehát:

A m(T) és n(T) képletének felírásához definiáljuk az ún. felületi integrál fogalmát. Legyen egy felület T tartományán értelmezett f skalár-vektor függvény. Osszuk fel a tartományt részekre, az i-edik rész felszíne legyen DT_i. Jelölje f_i a függvény értékét az i-edik felületdarab valamelyik pontjában. Képezzük a S f_i ×DT_i összeget. Ha a felosztás minden határon túli finomítása esetén ezen összegnek van határértéke, akkor ezt a határértéket felületi integrálnak nevezzük és

-vel jelöljük.

A felületi integrál általános alakja gömb alapfelület esetén:

, illetve b pólustávolságot használva j helyett:

Ha a T tartomány egy foktrapéz, akkor a felületi integrál az alábbi alakot ölti:

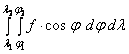, illetve b pólustávolságot használva j helyett:

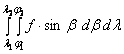
Térjünk vissza a területtorzulási arány meghatározásához. A T tartomány képének területét megkaphatjuk úgy, hogy a tartomány felosztása után minden egyes DT_i felszíndarabot egy pontjának területtorzulási modulusával beszorozzuk és az így kapott szorzatokat összeadjuk. Tudjuk, hogy

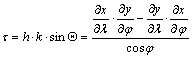
Ekkor - a t területtorzulási modulust az alapfelület pontjain értelmezett függvénynek tekintve - a keresett mennyiség egy felületi integrálként fogható fel, tehát m(T) és n(T) az alábbi módon írható fel:

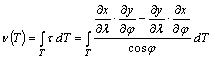
és

Gömbfelület esetén az alábbi képlet adja meg a területtorzulási arány képletét:

.

Ez foktrapéz esetén a következő alakot ölti:

.

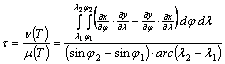Átlagos hossztorzulási arány

A hossztorzulási arányokat egy T tartományon átlagolhatjuk is, a következő módon. Rögzítsünk egy P(j_P,l_P)ÎT pontot, és minden Q(j_Q,l_Q)ÎT ponthoz rendeljük hozzá a P és Q pontokat összekötő ortodrómák l hossztorzulási arányát. Így egy l(Q) függvényt értelmeztünk a T tartományon, melynek értékeit egy felületi integrál segítségével átlagolhatjuk T-re:

Ez az átlag viszont hasonlóképpen függvénye a P pontnak, amelynek értékeit az iménti módon újra átlagolhatjuk T-re. A végeredményben kapott L mennyiség a T tartomány bármely két pontját összekötő ortodrómát hossztorzulási arányának az átlagát adja meg:

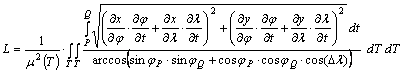
Ha az alapfelület gömb, a vizsgált T tartomány foktrapéz, továbbá az ortodrómák képének hosszát egyszerűen a (j ,l) és (u,v) koordinátákkal adott végpontokat összekötő egyenes szakasz hosszával mérjük, akkor az alábbi egyszerűbb közelítő képletet kapjuk:

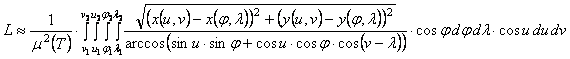
Ezzel a képlettel Aribert Peters német kartográfus vizsgálta világtérképek hossztorzulását.

A torzultság lokális jellemzése

Torzultság alatt a torzulásmentes állapottól való eltérés mértékét értjük, melyet a térkép egy pontjában számszerűleg az e² függvény ad meg. e² értéke akkor és csak akkor zérus, ha a vizsgált torzulás a pontban nem lép fel, és értéke annál nagyobb, minél erősebb az illető torzulás a pontban. Minthogy a hossz-, szög- és területtorzulások a térkép bármely pontjában kiszámíthatók a torzulási ellipszis adataiból, a torzultságot e²=e²(a,b) alakban célszerű vizsgálni.

A hossztorzultság lokális mértéke

A hossztorzultság mértékét a térkép egy pontjában akarjuk jellemezni egy számértékkel. A hossztorzulási modulus mint infinitezimálisan kicsiny ívhosszak hányadosa, irányfüggő. Ha egy pontra jellemző, iránytól független értékhez akarunk jutni, akkor e hányadost minden lehetséges irányra nézve átlagolni kell. Ehhez vegyünk tehát a térkép egy pontjában egy irányt, melynek az első vetületi főiránnyal bezárt szöge J. Ekkor az ebbe az irányba fellépő l hossztorzulás az alábbi képlettel számítható:

A hossztorzulás mértéke az |l‑1| nagyságától függ. A vizsgált pontban az átlagos hossztorzulás mértéke ekkor ‑ a nehézkesen kezelhető abszolút érték négyzetre emeléssel való helyettesítése után ‑ az ún. Jordan féle mérőszámmal adható meg:

(Szögtartó vetületeknél speciálisan l=a=b minden irányban, azaz a hossztorzulási modulust nem szükséges különböző irányokra átlagolni.)

A Jordan féle mérőszám alapötletét fejlesztette tovább Kavrajszkij. Abból a megfontolásból indult ki, hogy az (l–1)² kifejezés l=1+d esetén tetszõleges d‑választással ugyanazt az értéket adja, mint l=1‑d esetén, márpedig torzulási szempontból ezek nem tekinthetők egyenértékűeknek. (l=1.5 és l=0.5 közül pl. az utóbbi minősíthető kedvezőtlenebb hossztorzulásnak.) Ehelyett azt javasolta, hogy egy 1‑nél kisebb és egy 1‑nél nagyobb hossztorzulást akkor tekintsünk egyenértékűnek, ha az egyik 1‑nél annyiszor nagyobb, ahányszor

kisebb a másik (vagyis ha egymás reciprokai). Felhasználva, hogy

,

Kavrajszkij az (l–1)² kifejezést Ln²l‑ lel helyettesítette. Ebből kapható meg a vizsgált pontra vonatkozó átlagos hossztorzulás javított mértéke, az ún. Jordan‑Kavrajszkij féle mérőszám:

A területtorzultság lokális mértéke

Az egy pontra vonatkozó – és infinitezimálisan kicsiny mennyiségek hányadosából adódó –

területtorzulási modulus a

képlettel számítható. A területtorzulás területnagyobbodást vagy területcsökkenést jelent; ennek mértéke a területtartást jelentő t=1 értéktől való eltérés nagyságától függ. Ha az abszolút értékben egyező pozitív és negatív eltérést ugyanolyan kedvezőtlennek tekintjük, akkor a területtorzultság mértékét egyszerűen a területtartást jelentő t=1 értéktől való eltérés négyzetével adhatjuk meg:

Ez a mérték G. B. Airy múlt századi angol csillagásztól származik.

A területtorzulási mérőszámra alkalmazható a Kavrajszkij féle módosítás:

A szögtorzultság lokális mértéke

A helyfüggő területtorzulással szemben az i szögtorzulás egy tetszőleges pontban függ még a szögszárak irányától is. Tudjuk viszont, hogy minden olyan alapfelületi J szög i_J torzulása, melynek egyik szára az első vetületi főirányba mutat, i_J =b/a alakban írható, vagyis a J iránytól független konstans. A b/a mennyiség használata azonban korlátos (£1) volta miatt a szögtorzulás mértékéhez nem célszerű; erősebben torzult szögek esetén kifejezőbb a reciproka (a/b), amely akármekkora (³1) értéket felvehet. Ekkor a szögtorzulás mértéke (amely szintén Airytől származik [1]):

A szögtorzultság mértékének Kavrajszkij típusú alakja:

Megjegyezzük, hogy egy tetszőleges pontban fellépő extremális hossztorzulások (a és b) értéke egy sor vetületcsaládnál egyszerű képlettel közvetlenül megadható, azonban nem mindig dönthető el ránézésre, hogy közülük melyik a nagyobb (vagyis a maximális). Ezért az ilyen esetekben az a/b konkrét meghatározásához szükséges egy diszkusszió közbeiktatása.

A szögtorzulás mértékének megadásához azonban nem az a/b az egyetlen lehetséges kiindulási érték; az irányfüggőség miatt ez a kérdés sokfelől közelíthető meg. Alkalmazzák így szögtorzulási mérőszámként a valamely térképi pontban fellépő 2w maximális szögtorzulás értékét, amely tulajdonképpen szintén a/b egy függvénye:

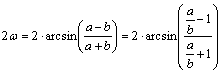
(a³b miatt 2w³0 mindig teljesül.)

Ennek a mennyiségnek is az a hibája, hogy felülről korlátos (2w£180°), és így a nagymértékû szögtorzulásokat a kelleténél kevésbé minősíti rossznak, nem differenciálja őket eléggé.

Végül a szögtorzulást ‑ irányfüggése miatt ‑ a Jordan féle mérőszámhoz hasonló módon jellemezhetjük a különböző irányokban fellépő szögtorzulások irány szerinti integrálja

segítségével. Frolov ehhez az első vetületi főiránnyal bezárt J alapfelületi iránynak J' képfelületi megfelelőjétől való négyzetes eltérését integrálta:

A teljes torzultság lokális mértéke

Ismeretes, hogy a kvantitatíve vizsgált torzulások közül a hossztorzulások ‑ egy vagy több hossztartó ponttól illetve vonaltól eltekintve ‑ mindig fellépnek a térképen; a területtorzulás vagy a szögtorzulás közül viszont az egyik kiküszöbölhető. A teljes torzulásnak mindenféle lokális jellegű torzulást tartalmaznia kell. Igen nehéz azonban mennyiségileg összevetni egyrészről az egymással szemben ható és ilyen értelemben összekapcsolható szög‑ és területtorzulásokat, másrészről a teljesen más jellegű hossztorzulásokat. A teljes torzultságnak ezért az optimális

vetületek elméletében két különböző értelmezése fordul elő.

Az egyik értelmezés a hossztorzulásokat tekinti a szög‑ és területtorzulások következményének, és a teljes torzulás fogalmát e két utóbbi együttesére szűkíti le. A másik értelmezés szerint a hossztorzulások az elsődlegesek, és ezekből erednek a szög‑ és területtorzulások; a teljes torzultsághoz eszerint elegendő valamilyen módon a hossztorzultságokra szorítkozni.

A második értelmezés ilyen módon visszavezet a hossztorzultságok vizsgálatához. A továbbiakban itt az első értelmezésben foglalkozunk a teljes torzultsággal: vagyis a kétféle torzultságot összegezzük.

A legkorábbi ismert teljes torzulási mérőszámot Airy vezette be idézett művében a szög- és területtorzultsági mutatók összegeként:

Ez az eredeti ún. Airy féle mérőszám, amelyet azonban maga Airy közvetlenül nem használt, hanem áttért az a,b‑ben szimmetrikus és egyszerűbb alakú

ún. Airy‑James-Clarke féle mérőszámra..

Az Airy féle mérőszám tovább finomítható egy további diszkusszió beépítésével, ha a szögtorzulást jellemző a/b értékhez hasonlóan a területtorzulás jellemzőjére is csak 1‑nél nagyobb értéket fogadunk el; ekkor tehát a fenti képletbe a*b helyett max {a*b, 1/(a*b)} írandó, ami bármely konkrét a,b számpár esetén a {} zárójelben lévő két mennyiség közül a nagyobbat jelenti.

Ekkor e²_AM³e²_AE, és speciálisan a területtartó, valamint a területcsökkenést sehol sem mutató vetületekre e²_AM=e²_AE.

Az eredeti Airy féle mérőszám a szög‑ és területtorzulást egyenlő súllyal szerepelteti. Szükség lehet azonban a teljes torzulás olyan vizsgálatára, amelynek során valamelyik résztorzulást a másiknál nagyobb mértékben tekintjük kedvezőtlennek, azaz nagyobb súllyal kívánjuk figyelembe venni. Erre ad lehetőséget a torzulási mérőszámok Klingatsch féle általánosítása, amely a két résztorzulásnak a súlyozott átlagával dolgozik:

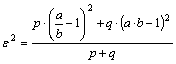
ahol a p és q(>0) súlyokat annak megfelelően írhatjuk elő, hogy a résztorzulások jelentőségével szemben milyen kívánalmakat támasztunk.

Alkalmazzuk a Kavrajszkij féle módosítást az eredeti Airy féle mérőszámra:

Ennek 2‑vel való osztása útján jutunk az a,b‑ben szintén szimmetrikus ún. Airy‑Kavrajszkij féle mérőszámhoz:

A Klingatsch féle általánosítás alkalmazható az Airy‑Kavrajszkij féle mérőszámhoz vezető kiindulási formulára:

A torzultsági kritériumok

A torzulási arányokhoz hasonlóan szeretnénk véges nagyságú alapfelületi idomokhoz torzultsági értéket is rendelni. Ezt megvalósíthatjuk pl. a pontonkénti lokális torzultsági értékek átlagolásával. Az E² átlagot a T tartományra vonatkozólag az e² függvény felületi integráljával összegezzük, és osztjuk a T tartomány m(T) felszínével:

A hossztorzultság átlagos mértékeként tehát a Jordan féle mérőszám alapján kapjuk az ún. Jordan féle kritériumot:

A Jordan-Kavrajszkij féle mérőszámból hasonlóan kapjuk a Jordan-Kavrajszkij féle kritériumot:

A területtorzultság átlagos mértékeként jutunk egy Airy típusú kritériumhoz:

és egy Kavrajszkij típusú kritériumhoz:

Hasonlóan kapjuk a szögtorzultság átlagos mérőszámait, nevezetesen az Airy típusút:

és a Kavrajszkij típusút:

A teljes torzultság átlagos mértékeként szolgál az eredeti Airy kritérium:

és ennek módosítása:

valamint a Kavrajszkij kritérium:

Végül - hibásan - itt szokták megemlíteni az Airy-James-Clarke kritériumot:

A teljes torzultság Klingatsch féle mérőszámának ismert az Airy típusú:

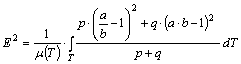
és a Kavrajszkij típusú változata:

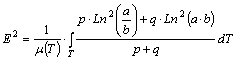
A felsorolt átlagos torzultsági mérőszámok nem egyforma hatékonysággal alkalmazhatók a vetületek torzultságának vizsgálatához; a közülük való választás függ a vetülettel szemben támasztott követelményektől, az ábrázolt terület nagyságától és elhelyezkedésétől, és esetleg a vizsgált vetületek torzulási sajátosságaitól.

A teljes Föld, illetve igen nagy kiterjedésű terület torzultsági vizsgálata esetén elsősorban a Kavrajszkij típusú mérőszámok használata javasolt; szintén megfelelő eredményt ad az Airy típusú mérőszámok módosított alakja. Az Airy-James-Clarke kritérium csak az izodeformációs öv környékén alkalmazható. Olyan vetületeknél, ahol az a,b közül valamelyik a végtelenhez tart, szintén a Kavrajszkij típusú mérőszámokkal célszerű dolgoznunk.