Great and small circles on the sphere
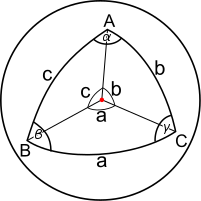
Spherical triangle


Using the denotations on the figure, the following identities apply to all spherical triangles:
Derivations can be found e.g. here.
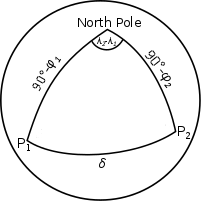
Let's find the spherical distance between points P1 (φ1, λ1) and P2 (φ2, λ2)! Considering the spherical triangle of P1, P1 and the North Pole (see figure) and using the cosine rule for the side δ, we get the following formula:
cos δ = cos(90°-φ1) cos(90°-φ2) + sin(90°-φ1) sin(90°-φ2) cos(λ2-λ1)
As cos(90°-x) = sin x and sin(90°-x) = cos x, we can use a simplified form:
cos δ = sin φ1 sin φ2 + cos φ1 cos φ2 cos(λ2-λ1),
where δ is the spherical distance of the two points on a unit sphere.
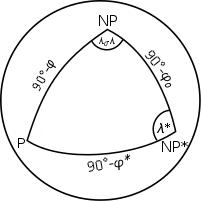
Let's define a meta coordinate system with meta pole at the point NP* (φ0, λ0), having the geodesic towards the true North Pole (NP) as prime meridian. The (φ*, λ*) metacoordinates of any P (φ, λ) point can be calculated by considering the spherical triangle P NP NP* (see figure):
sin φ* = sin φ sin φ0 + cos φ cos φ0 cos(λ0-λ),
sin φ = sin φ* sin φ0 + cos φ* cos φ0 cos λ*, from which cos λ* can be expressed:
cos λ* = ( sin φ - sin φ* sin φ0 ) / ( cos φ* cos φ0 )