Időpont, helyszín
Kedd 14:00–15:30 É 7.87 Rajzterem
Tematika
A tantárgyat szabadon választható kredit terhére felvett hallgatók számára erősen javasolt az azonos nevű előadás fölvétele; a két tananyag egymáshoz szorosan kapcsolódik. A tantárgy különösebb előismeretet nem igényel. A kurzus azoknak a hallgatóknak hasznos, akiknek szükséges a magyarországi topográfiai térképek koordináta-rendszere mögötti matematika mélyebb megértése.
Ajánlott irodalom: Györffy János: Térképészet és Geoinformatika II. tankönyv, hálózati jegyzetek: http://www.agt.bme.hu/staff_h/varga/Osszes/Dok3uj.htm és http://mercator.elte.hu/~gyorffy/jegyzete/jegyzBSc.html
Szükséges felszerelés
A gyakorlaton trigonometrikus függvényeket ismerő számológép (Javasolt típus: https://www.youtube.com/watch?v=ER4jGKlOOIE), íróeszköz és jegyzetfüzet használata kötelező. A számológép a gyakorlati órákon akkor váltható ki okostelefonnal, ha azon van inverz trigonometrikus függvényeket ismerő alkalmazás. A zárthelyi dolgozatok során csak számológép használható, telefon nem.
Számonkérés
- Kis ZH a félév közepén. Elérhető 20 pont. Sikeres kis ZH minimum 10 pont. A kis ZH 45 perces, számológép kivételével semmilyen segédeszköz nem használható. Részletek lejjebb.
- Nagy ZH a félév végén. Elérhető 40 pont. Sikeres nagy ZH minimum 16 pont. A nagy ZH során számítógép, jegyzet, tankönyv stb. használható, de mobiltelefon és internet nem (H:\ meghajtó sem). Internetes segédanyagait saját lemezre előre letöltve használhatja.
- Beadandók. A félév során 10, egyenként 3 pontot érő beadandó feladatot adok, határidejük a következő gyakorlati óra napján délután négy. Ha valaki nem tud megjelenni az órán, a feladat szövegét személyesen a fogadóórában vagy e-mailben kérheti el tőlem.
Elégséges osztályzathoz a 90-ből 40 pontot kell összesen összegyűjteni a félév végére. A két ZH közül az egyiket a póthéten javíthatja. (Rontani nem lehet.) Ha mindkét ZH sikertelen, pótZH-t nem írhat, osztályzatát gyakUV-n (szóbeli vizsga) javíthatja. A gyakUV törli a korábban összegyűjtött pontokat.
A félévközi kis ZH-ra a következő állandókat és képleteket kötelező fejből megtanulni (a vastag betűsek hiányos ismerete automatikusan sikertelen ZH-t jelent, a többi részt nem pontozom):
- A Föld sugara
- Pitagorasz-tétel
- Szögmértékegységek átváltása (csak fok, perc, másodperc és radián között)
- Sikbeli koszinusz- és szinusztétel
- Síkbeli derékszögű és polárkoordináták közötti átszámítás
- Gömbi szinusz- és koszinusztételek
- Foktrapéz felszíne (csak gömbön)
- Loxodróma hossza, azimutja (csak gömbön)
- Lapultság és első excentricitás definíciója, átszámítás
Isten ments, hogy a fenti képleteket ész nélkül ráírja a ZH-papírra!!! Valamennyi ZH-példa a gyakorlatokon megoldottakhoz hasonló szöveges feladat; rá kell jönni, hogy melyik képlet melyik feladat megoldásához szükséges. Ezek közül nem az összes képlet szükséges ténylegesen az igazi kis ZH-n; de cserkész becsületszavamra, olyan képletre nem kérdezek rá, amely itt nincs megemlítve. Ezek a képletek mellesleg véletlenül az év végi ZH-ba is belecsúszhatnak (igaz, akkor már lehet puskázni).
Hiányzások
Egy vagy két hiányzásnak nincs következménye. Három vagy négy hiányzás esetén az érintett órákon kiadott beadandókra beadandónként legalább 2 pontot kell elérni. Öt hiányzásnál gyakorlati jegy nem adható.
Hosszúpuska
Alább következik néhány képlet, amely a második ZH-n akár jól is jöhet. (Nem feltétlenül csak ezekre a képletekre lehet szükség, használja saját jegyzeteit is!)
A konstansok forrása: Varga J (2014): A vetületnélküli rendszerektől az UTM-ig
Szögtartó gömbvetület
Direkt:$$\varphi=2\operatorname{arctg}\left[\varkappa\operatorname{tg}^n\left(45°+\frac\varPhi2\right)\left(\frac{1-e\sin\varPhi}{1+e\sin\varPhi}\right)^\frac{ne}2\right]-90°$$$$\lambda=n\left(\varLambda-\varLambda_0\right)$$
Inverz:$$\varPhi''=2\operatorname{arctg}\sqrt[n]{\frac{\operatorname{tg}\left(45°+\frac\varphi2\right)}{\varkappa\left(\frac{1-e\sin\varPhi'}{1+e\sin\varPhi'}\right)^\frac{ne}2}}-90°$$$$\varLambda=\varLambda_0+\frac\lambda n$$
| Jelölés | Régi gömbi vetület | Új gömbi vetület | |
|---|---|---|---|
| Alapfelület | — | Bessel-ellipszoid | IUGG1967-ellipszoid |
| Képfelület | — | Régi Gauss-gömb | Új Gauss-gömb |
| Félnagytengely | a | 6 377 397,155 m | 6 378 160 m |
| Félkistengely | b | 6 356 078,963 m | 6 356 774,516 m |
| Első numerikus excentricitás | e | 0,081 696 683 121 57 | 0,081 820 567 9407 |
| Gauss-gömb sugara | R | 6 378 512,966 m | 6 379 743,001 m |
| ϰ | 1,003 016 135 133 | 1,003 110 007 693 | |
| n | 1,000 751 489 594 | 1,000 719 704 936 | |
| Φn | 46° 32’ 43,410 35” | 47° 10’ 0,000 00” | |
| φn | 46° 30’ 0,000 00” | 47° 07’ 20,057 80” | |
| Ferrótól | Λ0 | 36° 42’ 53,5733” | — |
| Greenwichtől | Λ0 | 19° 03’ 07,5533” | 19° 02’ 54,8584” |
Fokhálózat-elforgatás
Segédpólus ismert:
$$\sin\varphi^\ast=\sin\varphi\sin\varphi_0+\cos\varphi\cos\varphi_0\cos\left(\lambda-\lambda_0\right)$$$$\operatorname{tg}\lambda^\ast=\frac{-\sin\left(\lambda-\lambda_0\right)}{\cos\varphi_0\operatorname{tg}\varphi-\sin\varphi_0\cos\left(\lambda-\lambda_0\right)}$$
$$\sin\varphi=\sin\varphi^\ast\sin\varphi_0+\cos\varphi^\ast\cos\varphi_0\cos\lambda^\ast$$$$\operatorname{tg}\left(\lambda-\lambda_0\right)=\frac{-\sin\lambda^\ast}{\cos\varphi_0\operatorname{tg}\varphi^\ast-\sin\varphi_0\cos\lambda^\ast}$$
Segédegyenlítő és kezdő-segédmeridián metszéspontja ismert:
$$\sin\varphi^\ast=\sin\varphi\cos\varphi_K-\cos\varphi\sin\varphi_K\cos\left(\lambda-\lambda_K\right)$$$$\operatorname{tg}\lambda^\ast=\frac{\sin\left(\lambda-\lambda_K\right)}{\sin\varphi_K\operatorname{tg}\varphi+\cos\varphi_K\cos\left(\lambda-\lambda_K\right)}$$
$$\sin\varphi=\sin\varphi^\ast\cos\varphi_K+\cos\varphi^\ast\sin\varphi_K\cos\lambda^\ast$$$$\operatorname{tg}\left(\lambda-\lambda_K\right)=\frac{\sin\lambda^\ast}{\cos\varphi_K\cos\lambda^\ast-\sin\varphi_K\operatorname{tg}\varphi^\ast}$$
| Jelölés | Budapest | Marosvásárhely | HÉR | HKR | HDR | EOV | |
|---|---|---|---|---|---|---|---|
| Ellipszoidi szélesség | Φ0 / ΦK | 47° 29’ 09,6380” | 46° 33’ 06,4273” | 48° 42’ 56,317 96” | 47° 08’ 46,726 66” | 45° 34’ 36,586 90” | — |
| Ellipszoidi hosszúság (Ferrótól, EOV esetén Greenwichtől) |
Λ0 / ΛK | 36° 42’ 53,5733” | 42° 03’ 20,9550” | 36° 42’ 53,573 330” | 36° 42’ 53,573 330” | 36° 42’ 53,573 330” | 19° 02’ 54,8584” |
| Gauss-gömbi szélesség | φ0 / φK | 47° 26’ 21,1372” | 46° 30’ 22,9804” | 48° 40’ 02,000 00” | 47° 06’ 00,000 00” | 45° 31’ 59,000 00” | 47° 06’ 0,0000” |
| Gauss-gömbi hosszúság (Gellérthegytől) |
λ0 / λK | 0° 0’ 0,00000” | + 5° 20’ 41,8290” | 00° 00’ 00,000 00” | 00° 00’ 00,000 00” | 00° 00’ 00,000 00” | 0° 0’ 0,00000” |
Sztereografikus vetület
Egyenlete:$$\beta^\ast=90°-\varphi^\ast$$$$\varrho=2R\operatorname{tg}\frac{\beta^\ast}2$$$$\beta^\ast=2\operatorname{arctg}\frac\varrho{2R}$$
Polárkoordináták és polgári rendszer átszámítás:$$Y=\varrho\sin\lambda^\ast$$$$X=-\varrho\cos\lambda^\ast$$$$\varrho=\sqrt{X^2+Y^2}$$$$\operatorname{tg}\lambda^\ast=\frac Y{-X}$$
Közvetlen oda-vissza képletek:
$$Y=-2R\frac{\sin\left(\lambda-\lambda_0\right)\cos\varphi}{1+\sin\varphi\sin\varphi_0+\cos\varphi\cos\varphi_0\cos\left(\lambda-\lambda_0\right)}$$$$X=-2R\frac{\sin\varphi\cos\varphi_0-\cos\varphi\sin\varphi_0\cos\left(\lambda-\lambda_0\right)}{1+\sin\varphi\sin\varphi_0+\cos\varphi\cos\varphi_0\cos\left(\lambda-\lambda_0\right)}$$
$$\varphi=\arcsin\frac{R\sin\varphi_0\left(1-t\right)-X\cos\varphi_0}{R\left(1+t\right)}$$$$\lambda=\operatorname{arctg}\frac{-Y}{R\cos\varphi_0\left(1-t\right)+X\sin\varphi_0}+\lambda_0$$
| Jelölés | Budapest | Marosvásárhely | Ivanics |
|---|---|---|---|
| C | 500 000 m | 600 000 m | 400 000 m |
Szögtartó hengervetület
Egyenletei:
$$Y=cR\lambda^\ast+Y_0$$$$X=cR\ln\operatorname{tg}\left(45°+\frac{\varphi^\ast}2\right)+X_0$$
Közvetlen oda-vissza képletek:
$$Y=cR\operatorname{arctg}\frac{\sin\left(\lambda-\lambda_K\right)}{\operatorname{tg}\varphi\sin\varphi_K+\cos\varphi_K\cos\left(\lambda-\lambda_K\right)}+Y_0$$
$$X=\frac{cR}2\ln\frac{1+\sin\varphi\cos\varphi_K-\cos\varphi\sin\varphi_K\cos\left(\lambda-\lambda_K\right)}{1-\sin\varphi\cos\varphi_K+\cos\varphi\sin\varphi_K\cos\left(\lambda-\lambda_K\right)}+X_0$$
$$\varphi=\arcsin\left[\frac{\left(t-1\right)\cos\varphi_K}{1+t}+\frac{2\sin\varphi_K}{1+t}\sqrt\frac t{1+z^2}\right]$$
$$\lambda=\operatorname{arctg}\frac{2z\sqrt\frac t{1+z^2}}{\left(1-t\right)\sin\varphi_K+2\cos\varphi_K\sqrt\frac t{1+z^2}}+\lambda_K$$
| Jelölés | HÉR / HKR / HDR | EOV |
|---|---|---|
| c | –1 | 0,999 93 |
| X0 | 0 m | 200 000 m |
| Y0 | 0 m | 650 000 m |
MGRS Magyarországon
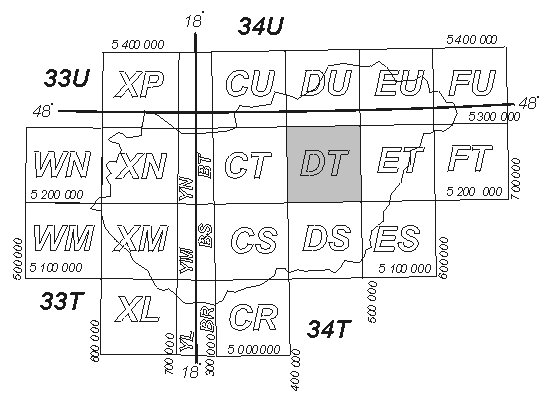
Átszámító táblák
Timár Gábor készített néhány Excel táblát, amellyel vetületi átszámításoket végezhetünk. A táblázatban szereplő képletek legjobb esetben is csak méteres pontosságot adnak!
